福建省2022届高三数学诊断性检测试卷
试卷更新日期:2022-04-12 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 的展开式中的常数项为( )A、-160 B、-80 C、80 D、1603. 设复数满足 , 且 , 则( )A、 B、 C、 D、4. 若 , 则“”的一个必要不充分条件是( )A、 B、 C、 D、5. 深度学习是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点的.在神经网络优化中,指数衰减的学习率模型为 , 其中表示每一轮优化时使用的学习率,表示初始学习率,表示衰减系数,表示训练迭代轮数,表示衰减速度.已知某个指数衰减的学习率模型的初始学习率为0.5,衰减速度为22,且当训练迭代轮数为22时,学习率衰减为0.45,则学习率衰减到0.05以下(不含)所需的训练迭代轮数至少为( )(参考数据: , )A、11 B、22 C、227 D、4816. 已知抛物线的焦点为 , 过且倾斜角为的直线交于A,两点,线段中点的纵坐标为 , 则( )A、 B、4 C、8 D、247. 关于函数 , 有下列四个命题:
甲:在单调递增;
乙:是的一个极小值点:
丙:是的一个极大值点;
丁:函数的图象向左平移个单位后所得图象关于轴对称.
其中只有一个是假命题,则该命题是( )
A、甲 B、乙 C、丙 D、丁8. 已知是定义在上的函数,且函数是奇函数,当时, , 则曲线在处的切线方程是( )A、 B、 C、 D、二、多选题
-
9. “杂交水稻之父”袁隆平一生致力于杂交水稻技术的研究、应用与推广,创建了超级杂交稻技术体系,为我国粮食安全、农业科学发展和世界粮食供给作出了杰出贡献.某杂交水稻种植研究所调查某地水稻的株高,得出株高(单位:)近似服从正态分布.已知时,有 , , .下列说法正确的是( )A、该地水稻的平均株高约为 B、该地水稻株高的方差约为100 C、该地株高超过的水稻约占68.27% D、该地株高低于的水稻约占99.87%10. 若满足 , , 则可以是( )A、 B、 C、 D、π11. 在正方体中, , , 分别为棱 , , 的中点,平面 , , 直线和直线所成角为 , 则( )A、 B、的最小值为 C、 , , , 四点共面 D、平面12. 已知是直角三角形,是直角,内角、、所对的边分别为、、 , 面积为 , 若 , , , , 则( )A、是递增数列 B、是递减数列 C、存在最大项 D、存在最小项
三、填空题
-
13. 已知 , 是不共线的两个单位向量,则与的夹角为.14. 直线与曲线恰有2个公共点,则实数的取值范围为.15. 写出一个同时具有下列性质①②③的函数.
①定义域为;②值域为;③对任意且 , 均有.
16. 《缀术》是中国南北朝时期的一部算经,汇集了祖冲之和祖暅父子的数学研究成果.《缀术》中提出的“缘幂势既同,则积不容异”被称为祖暅原理,其意思是:如果两等高的几何体在同高处被截得的两截面面积均相等,那么这两个几何体的体积相等,该原理常应用于计算某些几何体的体积.如图,某个西晋越窑卧足杯的上下底为互相平行的圆面,侧面为球面的一部分,上底直径为 , 下底直径为 , 上下底面间的距离为 , 则该卧足杯侧面所在的球面的半径是;卧足杯的容积是(杯的厚度忽略不计).
四、解答题
-
17. 已知等比数列的首项为 , 前项和为 , 且成等差数列.(1)、求的通项公式;(2)、设 , 求数列的前10项和.(表示不超过的最大整数)18. 冬季两项是第24届北京冬奥会的比赛项目之一,它把越野滑雪和射击两种特点不同的竞赛项目结合在一起.其中男子个人赛的规则如下:
①共滑行5圈(每圈),前4圈每滑行1圈射击一次,每次5发子弹;
②射击姿势及顺序为:第1圈滑行后卧射,第2圈滑行后立射,第3圈滑行后卧射,第4圈滑行后立射,第5圈滑行直达终点;
③如果选手有发子弹未命中目标,将被罚时分钟;
④最终用时为滑雪用时、射击用时和被罚时间之和,最终用时少者获胜.
已知甲、乙两人参加比赛,甲滑雪每圈比乙慢36秒,甲、乙两人每发子弹命中目标的概率分别为和.假设甲、乙两人的射击用时相同,且每发子弹是否命中目标互不影响.
(1)、若在前三次射击中,甲、乙两人的被罚时间相同,求甲胜乙的概率;(2)、若仅从最终用时考虑,甲、乙两位选手哪个水平更高?说明理由.19. 如图,在三棱锥中,和均是边长为4的等边三角形.是棱上的点, , 过的平面与直线垂直,且平面平面.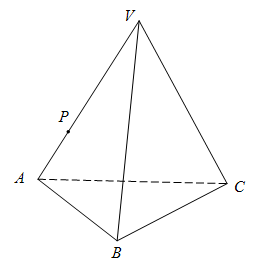 (1)、在图中画出 , 写出画法并说明理由;(2)、若直线与平面所成角的大小为 , 求过及点的平面与平面所成的锐二面角的余弦值。20. 的内角 , , 所对的边分别为 , , .(1)、求的大小;(2)、为内一点,的延长线交于点 , _________,求的面积.
(1)、在图中画出 , 写出画法并说明理由;(2)、若直线与平面所成角的大小为 , 求过及点的平面与平面所成的锐二面角的余弦值。20. 的内角 , , 所对的边分别为 , , .(1)、求的大小;(2)、为内一点,的延长线交于点 , _________,求的面积.请在下列三个条件中选择一个作为已知条件补充在横线上,使存在,并解决问题.
①为的外心,;
②为的垂心,;
③为的内心,.