河北省保定市安国市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四张扑克牌图案，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 语句“x的2倍与5的一半的差是非正数”可以表示为（　　）

A、2x $- \frac{5}{2} ＞$ 0 B、 $\frac{1}{2}$ （2x﹣5）≤0 C、2x $- \frac{5}{2} \leq$ 0 D、2x $- \frac{5}{2} \geq$ 0

查看试题解析
3. 下列从左到右的变形是因式分解且分解正确的是（　　）

A、（x+2y）（x﹣2y）＝x²﹣4y² B、x²+2x+1＝x（x+2）+1 C、4x²+8x+4＝4 （x²+2x+1） D、﹣8x²+8x﹣2＝﹣2（2x﹣1）²

查看试题解析
4. 如图，平行四边形ABCD中，E、F分别在边BC、AD上，添加条件后不能使AE＝CF的是（　　）

A、BE＝DF B、AE∥CF C、AF＝AE D、AF＝EC

查看试题解析
5. 如图，将 $△ A B C$ 绕点A逆时针旋转150°，得到 $△ A D E$ ，这时点B，C，D恰好在同一直线上，则 $∠ B$ 的度数为（）

A、10° B、15° C、20° D、30°

查看试题解析
6. 若关于x的分式方程 $\frac{x}{x - 1} - 2 = \frac{k}{1 - x}$ 有增根，则k的值为（　　）

A、1 B、0 C、﹣2 D、﹣1

查看试题解析
7. 如图，直线y＝x+m与y＝nx﹣5n（n≠0）的交点的横坐标为3，则关于x的不等式x+m＞nx﹣5n＞0的整数解为（）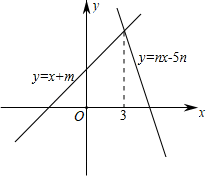

A、3 B、4 C、5 D、6

查看试题解析
8. 下面是涂涂同学完成的一组分式化简的练习题，每小题20分，他能得的分数是（　　）
① $\frac{x^{2} - 1}{x - 1} =$ x+1；②3﹣x• $\frac{2}{3 - x} =$ 2；③1 $\div \frac{a}{b} \times \frac{b}{a} =$ 1；④ $\frac{1}{x} + \frac{1}{y} = \frac{x + y}{x y}$ ；⑤（ $\frac{x}{x + 1} - x$ ） $\div \frac{x^{2} - x}{x + 1} = \frac{x - x^{2} + x}{x + 1} \div \frac{x^{2} - x}{x + 1} = \frac{x （ 2 - x ）}{x + 1}$ • $\frac{x + 1}{x （ x - 1 ）} = \frac{2 - x}{x - 1}$ ．

A、40分 B、60分 C、80分 D、100分

查看试题解析
9. 如图，在△ABC中，∠C＝90°，CB＝1，AC＝2，BD是∠ABC的角平分线，设△ABD和△BDC的面积分别是S₁ ， S₂ ，则S₁：S₂的值为（　　）

A、1：2 B、3：2 C、5： $\sqrt{5}$ D、 $\sqrt{5}$ ：1

查看试题解析
10. 如图，四边形ABCD是平行四边形，点E是平面内一点，且到AD，AB，BC三边所在直线的距离相等，则下列结论正确的是（　　）

A、∠AEB的度数不确定 B、符合条件的点E有两处 C、S_△AED＝S_△BEC，S_△AEB＝S_△CED D、点E在对角线AC 上

查看试题解析
11. 如图所示，在平行四边形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O，过点O作直线m交线段 $A B$ 于点E，交线段 $C D$ 于点F.则图中共有几对全等三角形（）

A、4 B、5 C、6 D、7

查看试题解析
12. 如图所示，将正五边形ABCDE的点C固定，并按顺时针方向旋转，要使新五边形A′B′CD′E′的顶点D′落在直线BC上，则旋转角度为（）

A、108° B、72° C、54° D、36°

查看试题解析
13. 如图，在▱ABCD中，AB $⊥$ AC，若AB=4，AC=6，则BD的长是（）

A、11 B、10 C、9 D、8

查看试题解析
14. 如图，在△ABC中，I是三角形角平分线的交点，O是三边垂直平分线的交点，连接AI，BI，AO，BO，若∠AOB＝140°，则∠AIB的大小为（　　）

A、160° B、140° C、130° D、125°

查看试题解析
15. 为了让更多的人接种新冠疫苗，某药厂疫苗生产线开足马力，24小时运转，该条生产线计划加工320万支疫苗，前五天按原计划的速度生产，五天后由于原料短缺，以原速度的一半生产，结果比原计划延期3天完成任务．设五天后每天生产x万支疫苗，则可列方程为（　　）

A、 $\frac{320 - 10 x}{2 x} = \frac{320 - 10 x}{x} - 3$ B、 $\frac{320 - 10 x}{x} = \frac{320 - 10 x}{2 x} - 3$ C、 $\frac{320}{2 x} = \frac{320}{x} + 3$ D、 $\frac{320}{2 x} = \frac{320}{x} - 3$

查看试题解析
16. 如图，点D是△ABC的边AB的中点，AB＜BC．用尺规作图在边AC上找一点E，使DE $= \frac{1}{2}$ BC，下列尺规作图正确的有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

17. 因式分解：2xy+9﹣x²﹣y²＝．
利用因式分解计算：（﹣2）²⁰²²+（﹣2）²⁰²¹﹣2²⁰²⁰＝．

查看试题解析
18. 如图，点E为平行四边形ABCD内一点，连接EA，EB，EC，AC，已知△BCE的面积为2，△ABE的面积为3，△CED的面积为10，则△ADE的面积为，阴影部分的面积为．

查看试题解析
19. 在如图所示的平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₂A₂B₁与△OA₁B₁关于点B₁成中心对称，再作△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，如此作下去，完成下列问题：

(1)、△B₄A₅B₅的顶点A₅的坐标是；

(2)、△B₂nA₂n₊₁B₂n₊₁（n是正整数）的顶点A₂n₊₁的坐标是．

查看试题解析

三、解答题

20. 解下列分式方程：

(1)、 $\frac{x - 2}{x - 3} = \frac{1}{2} + \frac{1}{3 - x}$ ；

(2)、 $\frac{x - 2}{x + 2} - 1 = \frac{16}{x^{2} - 4}$ ．

查看试题解析
21. 如图，在边长为1的小正方形组成的网格中，点A，B，O都在格点上．
（ 1 ）作出点A关于点O的对称点A₁；
（ 2 ）连接A₁B，画出线段A₁B绕点A₁顺时针旋转90°后得到的对应线段A₁B₁；
（ 3 ）连接AB₁ ，求四边形ABA₁B₁的面积．

查看试题解析
22. 上课时老师在黑板上书写了一个分式的符合题意化简结果，随后用手掌盖住了一部分，形式如下：
$• \frac{y^{2}}{x^{2} - x y} - \frac{y^{2} - x^{2}}{x^{2} - 2 x y + y^{2}} = \frac{x}{x - y}$

(1)、请你求出盖住部分化简后的结果；

(2)、当x＝3时，y等于何值时，原分式的值为5．

查看试题解析
23. 如图是一组正多边形．

(1)、观察每个正多边形中的∠α，完成下列表格：
正多边形的边数
3
4
5
6
……
n
∠α的度数
60°
45°
　　
　　
……
　　

(2)、根据规律，请你计算正十二边形中的∠α的度数；

(3)、是否存在正n边形使得∠α＝11°？若存在，请求出n的值，若不存在，请说明理由．

查看试题解析
24. 如图，在▱ABCD中，点E、F分别在BC、AD上，且BE＝DF．

(1)、求证：AE＝CF；

(2)、若AE平分∠BAD，BE＝3，求CD的长．

查看试题解析
25. 某种型号油电混合动力汽车，从A地到B地燃油行驶需纯燃油费用76元，从A地到B地用电行驶需纯用电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

(1)、求每行驶1千米纯用电的费用；

(2)、若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少需用电行驶多少千米？

查看试题解析
26. 如图，平面直角坐标系中，四边形ABCD是平行四边形，A（﹣3，0），B（3，0），C（0，4），连接OD，点E是线段OD的中点．

(1)、求点E和点D的坐标；

(2)、平面内是否存在一点N，使以C、D、E、N为顶点的四边形是平行四边形？若存在请求出点N的坐标；若不存在，请说明理由．

查看试题解析

正多边形的边数	3	4	5	6	……	n
∠α的度数	60°	45°			……