山西省太原市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 计算的结果为( )A、 B、 C、 D、2. 山西省教育厅官网是省教育厅在国际互联网上发布政务信息和提供在线服务的综合平台.下面是该官网上四个栏目的标志,其中的图案是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 如图,中, , , , 点D,E分别是 , 的中点,则的长为( )
3. 下列从左到右的变形,属于因式分解的是( )A、 B、 C、 D、4. 如图,中, , , , 点D,E分别是 , 的中点,则的长为( ) A、 B、 C、 D、5. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、6. 如图,将正六边形绕它的中点O顺时针旋转一定角度,可以使边与重合,则旋转角的最小度数为( )
A、 B、 C、 D、5. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、6. 如图,将正六边形绕它的中点O顺时针旋转一定角度,可以使边与重合,则旋转角的最小度数为( )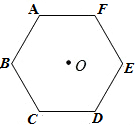 A、 B、 C、 D、7. 将不等式组的解集表示在数轴上正确的是( )A、
A、 B、 C、 D、7. 将不等式组的解集表示在数轴上正确的是( )A、 B、
B、 C、
C、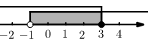 D、
D、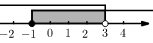 8. 如图,点P是内的一点,于点C,于点D,连接 , . 若 , 则下列结论不一定成立的是( )
8. 如图,点P是内的一点,于点C,于点D,连接 , . 若 , 则下列结论不一定成立的是( ) A、 B、 C、垂直平分 D、9. 四边形ABCD的对角线相交于点O,且 ,那么下列条件不能判断四边形ABCD为平行四边形的是( )A、 B、 C、 D、10. 学校组织八年级同学到劳动教育基地参加实践活动,某小组的任务是平整土地 . 开始的半小时,由于操作不熟练,只平整完 . 学校要求完成全部任务的时间不超过3小时,若他们在剩余时间内每小时平整土地 , 则x满足的不等关系为( )
A、 B、 C、垂直平分 D、9. 四边形ABCD的对角线相交于点O,且 ,那么下列条件不能判断四边形ABCD为平行四边形的是( )A、 B、 C、 D、10. 学校组织八年级同学到劳动教育基地参加实践活动,某小组的任务是平整土地 . 开始的半小时,由于操作不熟练,只平整完 . 学校要求完成全部任务的时间不超过3小时,若他们在剩余时间内每小时平整土地 , 则x满足的不等关系为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分式有意义的条件是 .12. 学校内的一条小路是用不同的多边形地砖铺成的.其中一块地砖的形状是七边形,则其内角和是 .
 13. 如图,中, , 将沿平移得到 , 与相交于点G,则的长为 .
13. 如图,中, , 将沿平移得到 , 与相交于点G,则的长为 . 14. 今年5月1日,历时8年修复的太原古县城正式开城迎客.统计结果显示,太原古县城第一时段a天内共接待游客m万人次,第二时段b天内共接待游客3m万人次,则这两个时段内平均每天接待游客万人次.15. 已知,中, , . 请从下列A,B两题中任选一题作答.、
14. 今年5月1日,历时8年修复的太原古县城正式开城迎客.统计结果显示,太原古县城第一时段a天内共接待游客m万人次,第二时段b天内共接待游客3m万人次,则这两个时段内平均每天接待游客万人次.15. 已知,中, , . 请从下列A,B两题中任选一题作答.、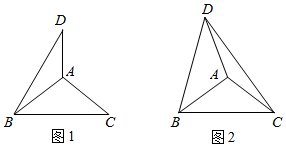
A.如图1,将线段绕点B逆时针旋转得到线段 , 连接 , 则的长为 .
B.如图2,将线段绕点B逆时针旋转得到线段 , 连接 , , 若 , 则的长为 .
三、解答题
-
16. 将下列各式分解因式:(1)、;(2)、 .17.(1)、先化简,再求值: , 其中;(2)、解方程: .18. 如图,已知 , 点A是射线上的一点.

( 1 )求作:直线l,使l经过点A,且于点B(要求:尺规作图,保留作图痕迹,不写作法);
( 2 )在(1)中线段的延长线上取点C,使 , 连接 . 按要求补全图形并证明 .
19. 如图,平面直角坐标系中,三个顶点的坐标分别为 , , .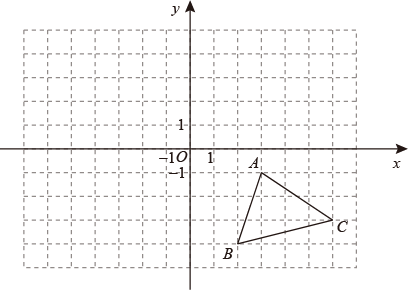
( 1 )请在图中画出与关于原点成中心对称的 , 并直接写出点 , , 的坐标: ▲ , ▲ , ▲ ;
( 2 )将点 , , 的横坐标分别加5,纵坐标分别减2,依次得到点 , , , 请在图中画出;
( 3 )若点是内的任意一点,点P经过(1)(2)中的两次变换后的对应点为 , 则点的坐标为 ▲ (用含m,n的式子表示).
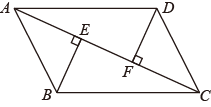
20. 已知:如图,在中,过点B,D分别作对角线的垂线,垂足为点E,F.求证: .
 21. “我是宝剑,我是火花,我愿生如闪电之耀亮,我愿死如彗星之迅忽.”这是山西党团组织的创始人高君宇的一首言志诗.在中国共产党成立100周年之际,八年级全体师生前往位于娄烦县峰岭底村的高君宇故居纪念馆参观.活动当天,大家在学校集合,号车先出发,小时后,号车沿同样路线出发,结果两辆车同时到达目的地.已知学校到高君宇故居纪念馆的路程是 , 号车的平均速度是号车平均速度的倍.
21. “我是宝剑,我是火花,我愿生如闪电之耀亮,我愿死如彗星之迅忽.”这是山西党团组织的创始人高君宇的一首言志诗.在中国共产党成立100周年之际,八年级全体师生前往位于娄烦县峰岭底村的高君宇故居纪念馆参观.活动当天,大家在学校集合,号车先出发,小时后,号车沿同样路线出发,结果两辆车同时到达目的地.已知学校到高君宇故居纪念馆的路程是 , 号车的平均速度是号车平均速度的倍. (1)、求1号车从学校到目的地所用的时间;(2)、参观结束之后,同学们分组进行了党史小剧场展演活动.为鼓励大家,学校决定从当地购买A,B两种纪念品共件奖励给参演同学.已知A种纪念品的单价为元/件,B种纪念品的单价为元/件,且A种纪念品数量不少于种的 . 求购买A种纪念品多少件可使购买纪念品的总价最少.22. 请阅读下列材料,完成相应的任务:
(1)、求1号车从学校到目的地所用的时间;(2)、参观结束之后,同学们分组进行了党史小剧场展演活动.为鼓励大家,学校决定从当地购买A,B两种纪念品共件奖励给参演同学.已知A种纪念品的单价为元/件,B种纪念品的单价为元/件,且A种纪念品数量不少于种的 . 求购买A种纪念品多少件可使购买纪念品的总价最少.22. 请阅读下列材料,完成相应的任务:无刻度直尺作图
“无刻度直尺”是尺规作图的工具之一,它的作用在于连接任意两点、作任意直线、延长任意线段.结合图形的性质,只利用无刻度直尺也可以解决一些几何作图问题.
如图1,已知:点P是线段的中点,分别以 , 为边在的同侧作与 , 其中 , , . 求作:线段的中点E.
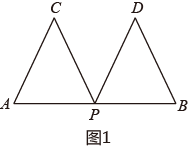
按照常规思路,用尺规作线段的垂直平分线,垂足即为的中点.仔细分析图形,你会发现,只用无刻度的直尺连接线段 , 与交点E即为的中点!(如图2).证明如下:连接 .
, . (依据1)

, .
同理, .
, , .
是的中点, .
, .
四边形是平行四边形.(依据2)
, 是的中点.
(1)、任务:写出上述证明过程中依据1与依据2的内容:依据1:;
依据2:;
(2)、如图3,在中,点E是边的中点,请利用无刻度直尺作图,保留作图痕迹,不写画法.
请从下面A,B两题中任选一题作答.我选择 ▲ 题.
A.求作: , 使的面积与的面积相等.
B.求作: , 使的面积与的面积相等.
23. 综合与实践
问题情境:数学课上,同学们以等腰直角三角形为背景探究图形变化中的数学问题.如图1,将两张等腰直角三角形纸片重叠摆放在桌面,其中 , , , 点A,D在的同侧,点B,C在线段上,连接并延长交于点O,已知 . 将从图1中的位置开始,绕点O顺时针旋转(保持不动),旋转角为 .
(1)、数学思考:“求索小组”的同学发现图1中 , 请证明这个结论;(2)、操作探究:如图2,当时,“笃行小组”的同学连接线段 , .请从下面A,B两题中任选一题作答.我选择 ▲ 题.
A.①猜想 , 满足的数量关系,并说明理由;
②若 , 请直接写出时,C,E两点间的距离;
B.①猜想 , 满足的位置关系,并说明理由;
②若 , 请直接写出点F落在延长线时,C,F两点间的距离.