山西省晋中市寿阳县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 下列手机手势解锁图案中,是中心对称图形的是( )A、
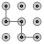 B、
B、 C、
C、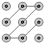 D、
D、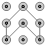 2. 下列各式中是分式的是( )A、 B、 C、 D、3. 已知分式的值为0,则( )A、x=1 B、x=﹣1 C、x>1 D、x>﹣14. 下列由左到右的变形,属于因式分解的是( )A、m2﹣4=(m﹣2)(m+2) B、(a+3)(a﹣3)=a2﹣9 C、t2﹣16﹣6t=(t+4)(t﹣4)﹣6t D、(m﹣2)(m﹣3)=(2﹣m)(3﹣m)5. 不等式2(x+1)<3x+1的解集在数轴上表示出来应为( )A、
2. 下列各式中是分式的是( )A、 B、 C、 D、3. 已知分式的值为0,则( )A、x=1 B、x=﹣1 C、x>1 D、x>﹣14. 下列由左到右的变形,属于因式分解的是( )A、m2﹣4=(m﹣2)(m+2) B、(a+3)(a﹣3)=a2﹣9 C、t2﹣16﹣6t=(t+4)(t﹣4)﹣6t D、(m﹣2)(m﹣3)=(2﹣m)(3﹣m)5. 不等式2(x+1)<3x+1的解集在数轴上表示出来应为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( )
6. 如图,小明想用皮尺测最池塘A、B间的距离,但现有皮尺无法直接测量,学习数学有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD=a,由此他即知道A、B距离是( ) A、a B、2a C、a D、3a7. 如图,在平行四边形ABCD中,CE⊥AB , E为垂足.如果∠BCE=28°,则∠D=( )
A、a B、2a C、a D、3a7. 如图,在平行四边形ABCD中,CE⊥AB , E为垂足.如果∠BCE=28°,则∠D=( )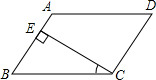 A、28° B、38° C、52° D、62°8. 若A,B为不等于0的整式,则下列各式成立的是( )A、(E为整式) B、(E为整式) C、 D、9. 关于x的分式方程=1有增根,则m的值为( )A、2 B、﹣2 C、﹣3 D、010. 已知▱ABCD,点E是边BC上的动点,以AE为边构造▱AEFG,使点D在边FG上,当点E由B往C运动的过程中,▱AEFG面积变化情况是( )
A、28° B、38° C、52° D、62°8. 若A,B为不等于0的整式,则下列各式成立的是( )A、(E为整式) B、(E为整式) C、 D、9. 关于x的分式方程=1有增根,则m的值为( )A、2 B、﹣2 C、﹣3 D、010. 已知▱ABCD,点E是边BC上的动点,以AE为边构造▱AEFG,使点D在边FG上,当点E由B往C运动的过程中,▱AEFG面积变化情况是( ) A、一直增大 B、保持不变 C、先增大后减小 D、先减小后增大
A、一直增大 B、保持不变 C、先增大后减小 D、先减小后增大二、填空题
-
11. 计算21×3.14+79×3.14的结果为 .12. 一个多边形的内角和是外角和的3倍,则它是边形.13. 如图,点D是直线 外一点,在 上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:
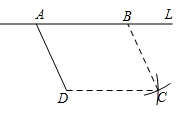 .14. 为了美化环境,某地政府计划对辖区内60km2的土地进行绿化,为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务,求原计划平均每月的绿化面积.甲同学所列的方程为 , 则甲同学所列方程中的x表示 .15. 将联结四边形对边中点的线段称为“中对线”.凸四边形ABCD的对角线AC=BD=4,且两条对角线的夹角为60°,那么该四边形较短的“中对线”的长度为 .
.14. 为了美化环境,某地政府计划对辖区内60km2的土地进行绿化,为了尽快完成任务,实际平均每月的绿化面积是原计划的1.5倍,结果提前2个月完成任务,求原计划平均每月的绿化面积.甲同学所列的方程为 , 则甲同学所列方程中的x表示 .15. 将联结四边形对边中点的线段称为“中对线”.凸四边形ABCD的对角线AC=BD=4,且两条对角线的夹角为60°,那么该四边形较短的“中对线”的长度为 . 16. 阅读某同学解分式方程的具体过程,回答后面问题.
16. 阅读某同学解分式方程的具体过程,回答后面问题.解方程 .
解:原方程可化为:
①
②
③
x=﹣6④
检验:当x=﹣6时,各分母均不为0,
∴x=﹣6是原方程的解.⑤
请回答:
(1)、第①步变形的依据是;(2)、从第步开始出现了错误,这一步不正确的原因是;(3)、原方程的解为 .三、解答题
-
17.(1)、解不等式组并写出它的最小整数解;(2)、因式分解:5x2﹣10x+5.(3)、化简: .(4)、解方程: .18. 化简: ,并在-3≤x≤2中选取一个你喜欢的整数x的值代入计算.19. 如图,E、F分别是平行四边形ABCD的边AD、BC上的点,且∠ABE=∠CDF.
求证:四边形BEDF是平行四边形.
 20. “居家嗨购,网上过年”,为做好疫情防控并促进春节线上消费,我省组织开展了2021“全晋乐购”网上年货节活动.某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工.该企业选购甲、乙两种物品,已知乙种物品单价是甲种物品单价的 , 购买9000元甲种物品的数量比购买4800元乙种物品的数量多10件.(1)、甲,乙两种物品的单价各为多少元?(2)、如果该企业购买甲,乙两种物品共150件,总费用不超过3.9万元,则购买甲种物品最多为多少件?21. 如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
20. “居家嗨购,网上过年”,为做好疫情防控并促进春节线上消费,我省组织开展了2021“全晋乐购”网上年货节活动.某企业采购了具有山西特色的年货慰问响应国家号召就地过年的员工.该企业选购甲、乙两种物品,已知乙种物品单价是甲种物品单价的 , 购买9000元甲种物品的数量比购买4800元乙种物品的数量多10件.(1)、甲,乙两种物品的单价各为多少元?(2)、如果该企业购买甲,乙两种物品共150件,总费用不超过3.9万元,则购买甲种物品最多为多少件?21. 如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形, (1)、观察上面每个正多边形中的∠α,填写下表:
(1)、观察上面每个正多边形中的∠α,填写下表:正多边形边数
3
4
5
6
……
n
∠α的度数
°
°
°
°
……
°
(2)、根据规律,计算正八边形中的∠α的度数.(3)、是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.22. 阅读下面的材料:常用的分解因式的方法有提取公因式法、公式法等,但有的多项式只用上述方法无法分解.如x2-4y2-2x+4y , 细心观察这个式子,会发现前两项符合平方差公式,后两项可提取公园式,前、后两部分分别分解因式后又出现新的公因式,提取公因式就可以完成整个式子的分解因式.具体过程如下:
x2-4y2-2x+4y
=(x2-4y2)-(2x-4y)
=(x+2y)(x-2y)-2(x-2y)
=(x-2y)(x+2y-2).
像这种将一个多项式适当分组后,进行分解因式的方法叫做分组分解法.
利用分组分解法解决下面的问题:
(1)、分解因式:x2-2xy+y2-4:(2)、已知△ABC的三边长a、b、c满足a2-ab-ac+bc=0,判断△ABC的形状并说明理由.23. 已知在▱ABCD中,动点P在AD边上,以每秒0.5cm的速度从点A向点D运动. (1)、如图1,在运动过程中,若CP平分∠BCD,且满足CD=CP,求∠B的度数.(2)、在(1)的条件下,若AB=4cm,求△PCD的面积.(3)、如图2,另一动点Q在BC边上,以每秒2cm的速度从点C出发,在BC间往返运动,P,Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=6cm,求当运动时间为多少秒时,以P,D,Q,B四点组成的四边形是平行四边形.
(1)、如图1,在运动过程中,若CP平分∠BCD,且满足CD=CP,求∠B的度数.(2)、在(1)的条件下,若AB=4cm,求△PCD的面积.(3)、如图2,另一动点Q在BC边上,以每秒2cm的速度从点C出发,在BC间往返运动,P,Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若AD=6cm,求当运动时间为多少秒时,以P,D,Q,B四点组成的四边形是平行四边形.