山西省大同市2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 2}$ 有意义，则x的取值范围是（　　）

A、x≥2 B、x≤2 C、x≥﹣2 D、x≤﹣2

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{(- 2)^{2}}$ ＝﹣2 B、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ C、 $(3 \sqrt{2})^{2} = 6$ D、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$

查看试题解析
3. 下列各组数中能作为直角三角形三边长的是（　　）

A、2，3，4 B、4，5，6 C、8，13，5 D、3，4，5

查看试题解析
4. 对于一次函数y＝﹣2x+4，下列结论正确的是（　　）

A、函数的图象与y轴的交点坐标是（4，0） B、函数的图象不经过第三象限 C、函数的图象向上平移4个单位长度得y＝﹣2x的图象 D、若A（x₁ ， y₁），B（x₂ ， y₂）两点在该函数图象上，且x₁＜x₂ ，则y₁＜y₂

查看试题解析
5. 如图，▱ABCD的对角线AC与BD相交于点O，∠BAC＝90°，AC＝6，BD＝10，则CD的长为（　　）

A、 $\sqrt{34}$ B、8 C、4 D、2

查看试题解析
6. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 和 $y = m x + n$ 相交于点 $(2 ， - 1)$ ，则关于 $x ， y$ 的方程组 ${\begin{matrix} y = k x + b \\ y = m x + n \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = - 1 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$

查看试题解析

7. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差，从这四人中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（）

运动员	甲	乙	丙	丁
平均数（ $c m$ ）	376	350	376	350
方差	12.5	13.5	2.4	5.4

A、甲 B、乙 C、丙 D、丁

查看试题解析

8. 如图，直线y＝kx+b（k≠0）经过点（2，0）和点（0，﹣3），当y＞0时，x的取值范围为（　　）

A、x＞2 B、x＞﹣3 C、x＞0 D、x＜2

查看试题解析
9. 已知在四边形ABCD中，AD∥BC，对角线AC与BD相交于点O，AO＝CO，如果添加下列一个条件后，就能判定这个四边形是菱形的是（　　）

A、BO＝DO B、AB＝BC C、AB＝CD D、AB∥CD

查看试题解析
10. 如图，一个条形测力计不挂重物时长5cm，挂上重物后，在弹性限度内弹簧伸长的长度与所挂重物的质量成正比，弹簧总长y（cm）关于所挂物体质量x（kg）的函数图象如图所示，则图中a的值是（　　）

A、15 B、18 C、20 D、33

查看试题解析

二、填空题

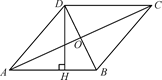
11. 关于x的方程kx+b＝0（k≠0）的解是x＝2，则一次函数y＝kx+b（k≠0）的图象与x轴的交点坐标是．

查看试题解析
12. 请写出一个y随x的增大而减小的正比例函数的表达式．

查看试题解析
13. 如图，四边形ABCD是菱形，AC＝16，DB＝12，DH⊥AB于点H，则DH等于．

查看试题解析
14. 在矩形ABCD中，对角线AC，BD相交于点O，若∠AOB＝60°，AB＝2，则BC的长为．

查看试题解析
15. 在平面直角坐标系中，矩形OABC的顶点O为坐标原点，顶点A，C分别在x轴和y轴上，OA＝4，OC＝3，D为AB边的中点，E是OA边上的一个动点，当△CDE的周长最小时，则点E的坐标为．

查看试题解析

三、解答题

16. 计算：

(1)、 $2 \sqrt{20} - \sqrt{5} + 2 \sqrt{\frac{1}{5}}$ ；

(2)、（ $\sqrt{2}$ + $\sqrt{3}$ ）²﹣（ $\sqrt{2}$ + $\sqrt{3}$ ）（ $\sqrt{2}$ ﹣ $\sqrt{3}$ ）．

查看试题解析
17. 已知点A（6，0）及在第一象限的动点P（x，10﹣x），设△OPA的面积为S．

(1)、求S关于x的函数解析式，并求出x的取值范围；

(2)、画出函数S的图象．

查看试题解析
18. 为声援扬州“运河申遗”，某校举办了一次运河知识竞赛，满分10分，学生得分为整数，成绩达到6分以上（包括6分）为合格，达到9分以上（包含9分）为优秀．这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示．

(1)、补充完成下面的成绩统计分析表：
组别
平均分
中位数
方差
合格率
优秀率
甲组
6.7
3.41
90%
20%
乙组
7.5
1.69
80%
10%

(2)、小明同学说：“这次竞赛我得了7分，在我们小组中排名属中游略偏上！”观察上表可知，小明是组的学生；（填“甲”或“乙”）

(3)、甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你给出两条支持乙组同学观点的理由．

查看试题解析
19. 阅读以下材料，并按要求完成相应的任务：
三角形中位线定理的证明

如图1，△ABC中，点D，E分别是AB，AC的中点，连接DE，像DE这样，连接三角形两边的中点的线段叫做三角形的中位线．求证：DE∥BC，且DE＝ $\frac{1}{2}$ BC．

证明：如图2，延长DE到点F，使EF＝DE，连接FC，DC，AF．

∵AE＝EC，DE＝EF，

∴四边形ADCF是平行四边形（依据1）．

∴CF//DA，CF=DA．

∵DA＝BD，

∴CF//BDA，CF=BD．

∴四边形DBCF是平行四边形（依据2）．

∴CF//BC，CF=BC．

∵DE＝ $\frac{1}{2}$ DF，

∴DE∥BC，且DE＝ $\frac{1}{2}$ BC．

归纳总结：

上述证明过程中运用了“倍长线段法”，也有人称材料中的方法为“倍长法”（延长了三角形中位线的一倍），该方法是解决初中数学几何题的一种常用方法．

(1)、任务（1）
上述材料证明过程中的“依据1”是指：；

“依据2”是指：；

(2)、类比探究
数学学习小组发现还可以用“倍长线段法”证明定理：直角三角形斜边上的中线等于斜边的一半．

已知：如图3，在Rt△ACB中，∠ACB＝90°，E为AB边的中点，求证：CE＝ $\frac{1}{2}$ AB．

证明：延长CE到点F，使EF＝CE，连接BF，AF，如图4．

任务（2）请将证明过程补充完整．

查看试题解析
20. 在新冠疫情防控期间，某校新购进A、B两种型号的电子体温测量仪共20台，其中A型仪器的数量不少于B型仪器的 $\frac{2}{3}$ ，已知A、B两种测温仪的价格如表所示，请问购买A、B两种测温仪各多少台时，可使所购仪器的总费用最少？最少需多少元？
型号
A
B
价格
800元/台
600元/台

查看试题解析
21. 综合与实践：
背景阅读：宽与长的比是 $\frac{\sqrt{5} - 1}{2}$ （约为0.618）的矩形叫黄金矩形．黄金矩形给我们以协调、匀称的美感．世界各国许多著名的建筑，为取得最佳的视觉效果，都采用的黄金矩形的设计，如希腊的帕特农神庙等．

实践操作：下面我们折叠出一个黄金矩形（如图所示）：

第一步：在一张矩形纸片的一端，利用图1的方法折出一个正方形，然后把纸展平．

第二步：如图2，把这个正方形折成两个相等的矩形，再把纸片展平．

第三步：折出内侧矩形的对角线AB，并把AB折到图3中所示的AD处．

第四步：展平纸片，按照所得的点D折出DE，矩形BCDE（图4）就是黄金矩形．

问题解决：

(1)、请在图1中证明四边形MNCB是正方形；

(2)、若MN＝2，请通过计算 $\frac{B E}{B C}$ 来说明矩形BCDE是黄金矩形．

查看试题解析
22. 如图，在平面直角坐标系中，直线AB分别交x轴，y轴于点A（3，0），点B（0，3）．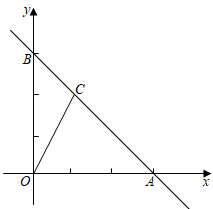

(1)、求直线AB的解析式；

(2)、若点C是线段AB上的一个动点，当△AOC的面积为3时，求出此时点C的坐标；

(3)、在（2）的条件下，在x轴上是否存在一点P，使得△COP是等腰三角形？若存在，直接写出所有满足条件的点P的坐标，若不存在，请说明理由．

查看试题解析

组别	平均分	中位数	方差	合格率	优秀率
甲组	6.7		3.41	90%	20%
乙组		7.5	1.69	80%	10%

型号	A	B
价格	800元/台	600元/台