河北省张家口市涿鹿县2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{1}{3}}$ C、 $\sqrt{10}$ D、 $\sqrt{0.3}$

查看试题解析
2. 以下列各组数的长度围成的三角形中，不是直角三角形的一组是（）

A、6，8，11 B、5，12，13 C、1， $\sqrt{3}$ ， 2 D、3，4，5

查看试题解析
3. 数据1、5、7、4、8的中位数是（）

A、4 B、5 C、6 D、7

查看试题解析
4. 已知点A的坐标为（2，-1），则点A到原点的距离为（）

A、3 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、1

查看试题解析
5. 当 $b < 0$ 时，一次函数 $y = x + b$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 下列计算正确的是（）

A、 $4 \sqrt{3} - 3 \sqrt{3} = 1$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} + \sqrt{8} = 3 \sqrt{2}$ D、 $3 + 2 \sqrt{2} = 5 \sqrt{2}$

查看试题解析
7. 如图，在正方形ABCD中，点E，F分别在CD，BC上，且AF=BE，BE与AF相交于点G，则下列结论中不正确的是（　　）

A、BF=CE B、∠DAF=∠BEC C、AF⊥BE D、∠AFB+∠BEC=90°

查看试题解析
8. 一次函数 $y = - 2 x + 3$ 的图象与两坐标轴的交点是（）

A、（0，3）（ $\frac{3}{2}$ ， 0） B、（1，3）（ $\frac{3}{2}$ ， 1） C、（3，0）（0， $\frac{3}{2}$ ） D、（3，1）(1， $\frac{3}{2}$ ）

查看试题解析
9. 一个圆桶底面直径为 $24 c m$ ，高 $32 c m$ ，则桶内所能容下的最长木棒为（）

A、 $50 c m$ B、 $45 c m$ C、 $40 c m$ D、 $38 c m$

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $∠ B A D = 80 °$ ， $A B$ 的垂直平分线交对角线 $A C$ 于点 $F$ ， $E$ 为垂足，连结 $D F$ ，则 $∠ C D F$ 等于（）

A、 $80 °$ B、 $70 °$ C、 $65 °$ D、 $60 °$

查看试题解析
11. 六箱救灾物资的质量（单位：千克）分别是17，20，18，17，18，18，则这组数据的平均数、众数、方差依次是（）

A、18，18，3 B、18，18，1 C、18，17.5，3 D、17.5，18，1

查看试题解析
12.
如图，在△ABC中，∠A=90°，AC=8，AB=6，点D是BC边上的动点（不与B，C重合）过点D作DE⊥AB于点E，作DF⊥AC于点F，则EF的最小值是（）

A、3 B、 $\frac{24}{5}$ C、5 D、 $\frac{11}{2}$

查看试题解析
13. 在 $▱ A B C D$ 中，E、F分别在 $B C$ 、 $A D$ 上，若想使四边形 $A F C E$ 为平行四边形，须添加一个条件，这个条件可以是（）
① $A F = C E$ ；② $A E = C F$ ；③ $∠ B A E = ∠ F C D$ ；④ $∠ B E A = ∠ F C E$ ．

A、①或② B、②或③ C、③或④ D、①或③或④

查看试题解析
14. 如图，是某蓄水池的横断面示意图，分深水区和浅水区，如果向这个蓄水池以固定的流量注水，图中哪个图像能大致表示水的最大深度 $h$ 和时间 $t$ 之间的函数关系（）

A、 B、 C、 D、

查看试题解析

二、填空题

15. 三边为9，12，15的三角形，其面积为．

查看试题解析
16. 若一列数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， …， $x_{n}$ 的方差是2，则数据 $x_{1} + 5$ ， $x_{2} + 5$ ， $x_{3} + 5$ ， …， $x_{n} + 5$ 的方差是．

查看试题解析
17. 如图，E是正方形 $A B C D$ 的对角线 $B D$ 上任意一点，四边形 $E F C G$ 是矩形，若正方形 $A B C D$ 的边长为n，则矩形 $E F C G$ 的周长为．

查看试题解析
18. 有甲、乙两个长方体的蓄水池，将甲池中的水匀速注入乙池，甲、乙两个蓄水池中水的高度y（米）与注水时间x（小时）之间的函数图象如图所示，若要使甲、乙两个蓄水池的蓄水深度相同，则注水的时间应为小时．

查看试题解析

三、解答题

19.

(1)、计算： $(\sqrt{24} - \sqrt{2}) - (\sqrt{8} + \sqrt{6})$

(2)、计算： $(\sqrt{2} - 1) (\sqrt{2} + 1) + {(\sqrt{3} - 2)}^{2}$

查看试题解析
20. 如图，在 $R t$ ⊿ $A B C$ 中， $∠ A C B = 90^{\circ}$ ， $C D ⊥ A B$ 于 $D$ ， $A C = 20 ， B C = 15$ .

(1)、求 $A B$ 的长；

(2)、求 $C D$ 的长.

查看试题解析

21. 我市某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.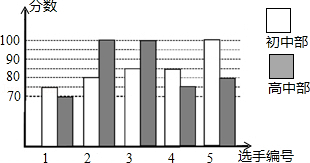

(1)、根据图示填写下表；

	平均数（分）	中位数（分）	众数（分）
初中部		85
高中部	85		100

(2)、结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；

(3)、计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

查看试题解析

22. 如图，在平行四边形 $A B C D$ 中，点E、F分别为边 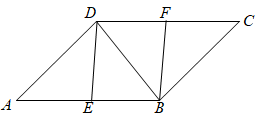$A B$ ， $C D$ 的中点，连接 $D E$ ， $B F$ ， $B D$ ．

(1)、求证： $△ A D E ≌ △ C B F$ ；

(2)、若 $∠ A D B = 90 °$ ，求证：四边形 $B F D E$ 为菱形．

查看试题解析
23. 某市对居民用水按“阶梯水价”方式进行收费，人均月生活用水收费标准如图所示．图中x表示人均月生活用水的吨数，y表示收取的人均月生活用水费（元），请根据图象信息，回答下列问题：

(1)、该市人均月生活用水的收费标准是：不超过5吨，每吨按元收取；超过5吨的部分，每吨按元收取；

(2)、请写出y与x的函数关系式．

查看试题解析
24. 如图，在平面直角坐标系中，矩形 $O A B C$ 的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为 $(6 ， 4)$ ， E为 $A B$ 的中点，过点 $D (8 ， 0)$ 和点E的直线分别与 $B C$ 、y轴交于点F，G．

(1)、求直线 $D E$ 的函数关系式；

(2)、函数 $y = m x - 2$ 的图象经过点F且与x轴交于点H，求出点F的坐标和m值；

(3)、在（2）的条件下，求出四边形 $O H F G$ 的面积．

查看试题解析