河北省张家口市宣化区2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 式子 在实数范围内有意义,则x的取值范围是( )A、x<-2 B、x>-2 C、x≥-2 D、x≤-22. 下列各数中,是勾股数的是( )A、0.3,0.4,0.5 B、6,8,10 C、 , , D、10,15,183. 下列计算不正确的是( )A、 B、 C、 D、4. 已知菱形的边长为5cm,一条对角线长为8cm,另一条对角线长为( )A、3cm B、4cm C、6cm D、8cm5. 矩形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、邻角互补 C、对角相等 D、对角线相等6. 关于函数y= -x-3的图象,有如下说法:
①图象过点(0,-3);②图象与x轴的交点是(-3,0);③由图象可知y随x的增大而增大; ④图象不经过第一象限;⑤图象是与y= -x+4平行的直线.其中正确的说法有( )
A、5个 B、4个 C、3个 D、2个7. 在我区举行的课堂比赛中,7位评委给某位选手的评分不完全相同.若去掉一个最高分,去掉一个最低分,则以下四个统计量中一定不会发生变化的是( )A、平均分 B、众数 C、中位数 D、方差8. 如图,有一个水池,水池的横截面是一边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池的一边,它的顶端恰好到达池边的水面,这根芦苇的长度为( )尺. A、10 B、12 C、13 D、149. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形10. 为了解某班学生每天使用零花钱的情况,小敏随机调查了15名同学,结果如表:
A、10 B、12 C、13 D、149. 若顺次连接四边形ABCD各边的中点所得四边形是菱形,则四边形ABCD一定是( )A、菱形 B、对角线互相垂直的四边形 C、矩形 D、对角线相等的四边形10. 为了解某班学生每天使用零花钱的情况,小敏随机调查了15名同学,结果如表:每天用零花钱(单位:元)
1
2
3
4
5
人数
2
4
5
3
1
则这15名同学每天使用零花钱的众数和中位数分别是( )
A、3,3 B、5,2 C、3,2 D、3,511. 下列图象中,可以表示一次函数 与正比例函数 (k,b为常数,且kb≠0)的图象的是( )A、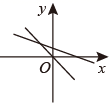 B、
B、 C、
C、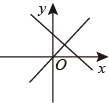 D、
D、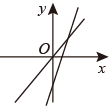 12. 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法不正确的是( )
12. 甲、乙两人在操场上赛跑,他们赛跑的路程S(米)与时间t(分钟)之间的函数关系如图所示,则下列说法不正确的是( ) A、甲、乙两人进行1000米赛跑 B、甲先慢后快,乙先快后慢 C、比赛到2分钟时,甲、乙两人跑过的路程相等 D、甲先到达终点
A、甲、乙两人进行1000米赛跑 B、甲先慢后快,乙先快后慢 C、比赛到2分钟时,甲、乙两人跑过的路程相等 D、甲先到达终点二、填空题
-
13. 一组数据3,2,1,4, 的平均数为3,则 的值是 .14. , 则的值为。15. 若y与成正比例,且当时, , 则y与x的函数解析式为y= .16. 在直角三角形中,若其中两条边的长分别为 , , 则第三边长为 .17. 如图,周长为的菱形中,点E、F分别在边、上, , , P为上一动点,则线段长度的最小值为 .
 18. 直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为 .
18. 直线:与直线:在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为 .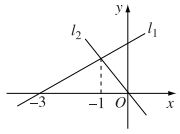
三、解答题
-
19. 计算: .20. 如图,网格中的 ,若小方格边长为1,请你根据所学的知识,
 (1)、判断 是什么形状?并说明理由;(2)、求 的面积.21. 如图,在矩形中,对角线 , 相交于点O,若 , , 求的长.
(1)、判断 是什么形状?并说明理由;(2)、求 的面积.21. 如图,在矩形中,对角线 , 相交于点O,若 , , 求的长. 22. 某篮球队对队员进行定点投篮测试,每人每次投篮10次,现对甲、乙两名队员在五次中进球数(单位:个)进行统计,结果如表:
22. 某篮球队对队员进行定点投篮测试,每人每次投篮10次,现对甲、乙两名队员在五次中进球数(单位:个)进行统计,结果如表:第1次
第2次
第3次
第4次
第5次
甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为3.2.
(1)、求乙进球的平均数和方差;(2)、如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?23. 如图,已知一次函数的图象经过 , 两点,并且交x轴于点C,交y轴于点D. (1)、求该一次函数的解析式;(2)、求的面积.24. 如图,在菱形中, , , 点E是边的中点.点M是边上一动点(不与点A重合),连接并延长交的延长线于点N,连接、 .
(1)、求该一次函数的解析式;(2)、求的面积.24. 如图,在菱形中, , , 点E是边的中点.点M是边上一动点(不与点A重合),连接并延长交的延长线于点N,连接、 . (1)、求证:四边形是平行四边形;(2)、当时,求证:四边形是矩形;(3)、填空:当的值为时,四边形是菱形.25. 习近平总书记说:“人民群众多读书我们的民族精神就会厚重起来、深邃起来。”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需元;购进6本A类图书和2本B类图书共需元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用元全部购进.两类图书,设购进A类x本,B类y本.
(1)、求证:四边形是平行四边形;(2)、当时,求证:四边形是矩形;(3)、填空:当的值为时,四边形是菱形.25. 习近平总书记说:“人民群众多读书我们的民族精神就会厚重起来、深邃起来。”某书店计划在4月23日世界读书日之前,同时购进A,B两类图书,已知购进3本A类图书和4本B类图书共需元;购进6本A类图书和2本B类图书共需元.(1)、A,B两类图书每本的进价各是多少元?(2)、该书店计划用元全部购进.两类图书,设购进A类x本,B类y本.①求y关于x的关系式;
②进货时,A类图书的购进数量不少于60本,已知A类图书每本的售价为38元,B类图书每本的售价为50元,若书店全部售完可获利W元,求W关于x的关系式,并说明应该如何进货才能使书店所获利润最大,最大利润为多少元?