河北省辛集市2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 下列实数中的无理数是( )A、0 B、 C、 D、1.01010101…2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 下列四组线段中,不能作为直角三角形三条边的是( )A、3,4,5 B、2,2, C、2,5,6 D、5,12,134. 小明的微信红包原有80元钱,他在新年一周里抢红包,红包里的钱随着时间的变化而变化,在上述过程中,自变量是( )A、时间 B、小明 C、80元 D、红包里的钱5. 已知P1(﹣1,y1),P2(2,y2)是一次函数y=﹣x+1图象上的两个点,则y1 , y2的大小关系是( )
A、y1=y2 B、y1<y2 C、y1>y2 D、不能确定6. 已知一组数据13,13,14,15,17,x的中位数是14.5,对于数据x的判断,正确的是( )A、 B、 C、 D、7. 如图,将三角尺ABC沿边BC所在直线平移后得到△DCE,连接AD,下列结论正确的是( )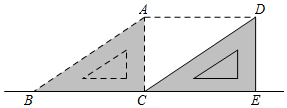 A、AD=AB B、四边形ABCD是平行四边形 C、AD=2AC D、四边形ABCD是菱形8. 如图,一棵大树在离地面3 ,5 两处折成三段,中间一段 恰好与地面平行,大树顶部落在离大树底部6 处,则大树折断前的高度是( )
A、AD=AB B、四边形ABCD是平行四边形 C、AD=2AC D、四边形ABCD是菱形8. 如图,一棵大树在离地面3 ,5 两处折成三段,中间一段 恰好与地面平行,大树顶部落在离大树底部6 处,则大树折断前的高度是( ) A、 B、 C、 D、9. 若某一样本的方差为 , 样本容量为5.则下列说法:①当时,;②该样本的平均数为7;③x,y的平均数是7;④该样本的方差与x,y的值无关.其中不正确的是( )A、①② B、②④ C、①③ D、③④10. 勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )A、
A、 B、 C、 D、9. 若某一样本的方差为 , 样本容量为5.则下列说法:①当时,;②该样本的平均数为7;③x,y的平均数是7;④该样本的方差与x,y的值无关.其中不正确的是( )A、①② B、②④ C、①③ D、③④10. 勾股定理是人类早期发现并证明的重要数学定理之一,这是历史上第一个把数与形联系起来的定理,其证明是论证几何的发端.下面四幅图中,不能证明勾股定理的是( )A、 B、
B、 C、
C、 D、
D、 11. 如图,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E,O,F.下列结论正确的个数有( )
11. 如图,在平行四边形ABCD中,对角线AC的垂直平分线分别与AD,AC,BC相交于点E,O,F.下列结论正确的个数有( )①四边形AFCE为菱形;
②ABF≌CDE;
③当F为BC中点时,∠ACD=90°.
 A、0个 B、1个 C、2个 D、3个12. 如图,已知直线与的交点的横坐标为-2,根据图象有下列3个结论:①;②;③是不等式 的解集
A、0个 B、1个 C、2个 D、3个12. 如图,已知直线与的交点的横坐标为-2,根据图象有下列3个结论:①;②;③是不等式 的解集 其中正确的个数是( ).
其中正确的个数是( ). A、0 B、1 C、2 D、313. 如图,在矩形中,F是中点,E是上一点,且 , , , 则矩形的面积为( )
A、0 B、1 C、2 D、313. 如图,在矩形中,F是中点,E是上一点,且 , , , 则矩形的面积为( ) A、16 B、 C、 D、14. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )
A、16 B、 C、 D、14. 如图1,在平面直角坐标系中, 在第一象限,且 轴.直线 从原点 出发沿x轴正方向平移.在平移过程中,直线被 截得的线段长度n与直线在x轴上平移的距离m的函数图象如图2所示.那么 的面积为( )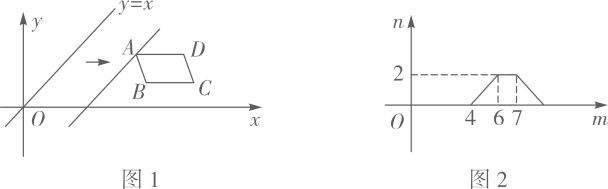 A、3 B、 C、6 D、
A、3 B、 C、6 D、二、填空题
-
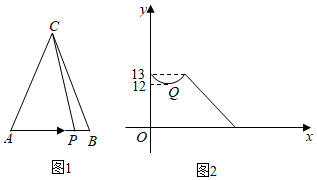
15. 函数中,自变量的取值范围是 .16. 已知a,b,c,d的平均数是3,则2a﹣1,2b﹣1,2c﹣1,2d﹣1的平均数是 .17. 如图1,点P从的顶点A出发,沿A→B→C匀速运动到点C,图2是点P运动时线段的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则的边的长度为 .
 18. 在正方形网格中,A , B , C , D , E均为格点,则∠BAC-∠DAE=°.
18. 在正方形网格中,A , B , C , D , E均为格点,则∠BAC-∠DAE=°. 19. 如图,两条互相垂直的线段、将正方形分割成①、②、③、④四块(图1),正好围成一个大正方形(图2),若 , , 则的长是 .
19. 如图,两条互相垂直的线段、将正方形分割成①、②、③、④四块(图1),正好围成一个大正方形(图2),若 , , 则的长是 .
三、解答题
-
20. 计算:(1)、;(2)、 .21. 如图,直线:交y轴于点 , 直线:交x轴于点 , 两直线交于点P,根据图中的信息解答下列问题:
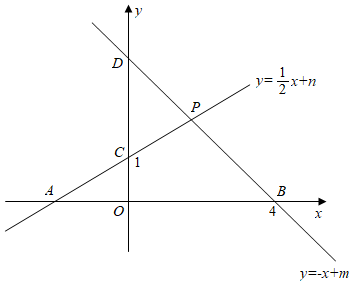 (1)、不等式的解集是 , 不等式组的解集是;(2)、求点P的坐标;22. 如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F.
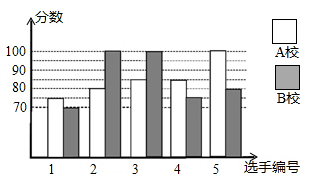
(1)、不等式的解集是 , 不等式组的解集是;(2)、求点P的坐标;22. 如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F. (1)、求证:四边形BEDF是菱形;(2)、若∠ABC=45°,∠ACB=30°,CD=6,求菱形BEDF的边长.23. 某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.
(1)、求证:四边形BEDF是菱形;(2)、若∠ABC=45°,∠ACB=30°,CD=6,求菱形BEDF的边长.23. 某市举行知识大赛,A校.B校各派出5名选手组成代表队参加比赛.两校派出选手的比赛成绩如图所示.根据以上信息.整理分析数据如表:
平均数/分
中位数/分
众数/分
A校
85
85
85
B校
85
a
b
 (1)、a=;b=;(2)、填空:(填“A校”或“B校”)
(1)、a=;b=;(2)、填空:(填“A校”或“B校”)①从两校比赛成绩的平均数和中位数的角度来比较,成绩较好的是;
②从两校比赛成绩的平均数和众数的角度来比较,成绩较好的是;
③从两校比赛成绩的方差的角度来比较,代表队选手成绩的方差较大.
24. 如图所示的正方形网格中,每个小正方形的边长为1,网格的中心标记为点O.按要求画四边形,使它的四个顶点均落在格点上,且点O为其对角线交点:
( 1 )在图1中画一个两边长分别为6和4的矩形;
( 2 )在图2中画一个平行四边形,使它有且只有一条对角线与(1)中矩形的对角线相等;
( 3 )在图3中画一个正方形,使它的对角线与(1)中所画矩形的对角线相等.
25. 某校为奖励本学年度表现优秀的学生,决定从某超市购买A、B两种商品,现有两种优惠购买方式如下:(不可同时参与)方式一:标价为100元的A商品打7折,标价为120元的B商品打85折;
方式二:若所购商品达到或超过101件(不同商品可累计),则按标价打8折.
若学校购买A商品x件(x为正整数),购买B商品的件数比A商品件数的2倍还多2件,方式一付款金额为 , 方式二付款金额为 .
(1)、请写出 , 与x之间的函数表达式;(2)、该校应该如何选择优惠方式,才能获得最大优惠?请说明理由;(3)、该单位购买A商品50件,B商品多少件?此时按最大优惠的付款金额为多少元?26. 数学课上,李老师提出问题:如图1,在正方形ABCD中,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.求证:AE=EF.



经过思考,小聪展示了一种正确的解题思路.取AB的中点H,连接HE,则△BHE为等腰直角三角形,这时只需证△AHE与△ECF全等即可.
在此基础上,同学们进行了进一步的探究:
(1)、小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(不含点B,C)的任意一点”,其他条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点符合题意吗?如果符合题意,写出证明过程,如果不符合题意,请说明理由;(2)、小华提出:如图3,如果点E是边BC延长线上的任意一点,其他条件不变,那么结论“AE=EF”是否成立?(填“是”或“否”);(3)、小丽提出:如图4,在平面直角坐标系xOy中,点O与点B重合,正方形的边长为1,当E为BC边上(不含点B,C)的某一点时,点F恰好落在直线y=﹣2x+3上,请直接写出此时点E的坐标.