河北省唐山市遵化市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 某学校初、高六个年级共有名学生,为了了解其视力情况,现采用抽样调查,如果按的比例抽样,则样本容量是( )A、 B、 C、 D、2. 若正比例函数的图象经过点 , 则这个图像必经过点( )A、 B、 C、 D、3. 在平行四边形ABCD中,对角线AC、BD相交于点O,若SABCD=24,则S△AOB=( )A、3 B、4 C、5 D、64. 将某个图形的各个顶点的横坐标都减去2,纵坐标保持不变,可将该图形( )A、向左平移2个单位 B、向右平移2个单位 C、向上平移2个单位 D、向下平移2个单位5. 如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )A、6 B、11 C、12 D、186. 在四边形 中, ,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是( )A、 B、 C、 D、7. 下列函数关系式中,自变量x的取值范围不正确的是( )A、y=2x2中,x为全体实数 B、y=中,x≠﹣1 C、y=中,x=0 D、y=中,x>﹣78. 如图,表示A点的位置,正确的是( )
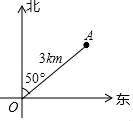 A、距O点3km的地方 B、在O点的东北方向上 C、在O点东偏北40°的方向 D、在O点北偏东50°方向,距O点3km的地方9. 下列调查最适合用查阅资料的方法收集数据的是( )A、班级推选班长 B、本校学生的到时间 C、2014世界杯中,谁的进球最多 D、本班同学最喜爱的明星10.
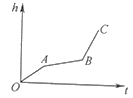
A、距O点3km的地方 B、在O点的东北方向上 C、在O点东偏北40°的方向 D、在O点北偏东50°方向,距O点3km的地方9. 下列调查最适合用查阅资料的方法收集数据的是( )A、班级推选班长 B、本校学生的到时间 C、2014世界杯中,谁的进球最多 D、本班同学最喜爱的明星10.均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
 A、
A、 B、
B、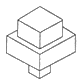 C、
C、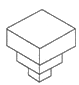 D、
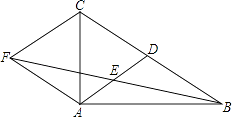
D、 11. 已知点 的坐标是 ,则点 关于 轴的对称点的坐标是( )A、 B、 C、 D、12. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
11. 已知点 的坐标是 ,则点 关于 轴的对称点的坐标是( )A、 B、 C、 D、12. 如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )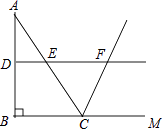 A、7 B、8 C、9 D、1013. 在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )
A、7 B、8 C、9 D、1013. 在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),则关于点D的说法正确的是( )甲:点D在第一象限
乙:点D与点A关于原点对称
丙:点D的坐标是(-2,1)
丁:点D与原点距离是.
A、甲乙 B、乙丙 C、甲丁 D、丙丁14. 如图,已知函数y=ax+b和y=kx的图像交于点P,则根据图像可得关于x,y的二元一次方程组的解是( ) A、 B、 C、 D、15. 已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为( , m),则不等式组mx﹣2<kx+1<mx的解集为( )A、x> B、 <x< C、x< D、0<x<16. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为( )
A、 B、 C、 D、15. 已知直线y1=kx+1(k<0)与直线y2=mx(m>0)的交点坐标为( , m),则不等式组mx﹣2<kx+1<mx的解集为( )A、x> B、 <x< C、x< D、0<x<16. 如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的面积为1,则第n个矩形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 依次连接菱形各边中点所得到的四边形是 .18. 教室里座位整齐摆放,若小华坐在第四排第6行,用有序数对(4,6)表示,则(2,4)表示的含义是 .19. 将直线y=﹣2x+3向下平移4个单位长度,所得直线的解析式为 .
三、解答题
-
20. 小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)、放入一个小球量筒中水面升高cm;(2)、求放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式(不要求写出自变量的取值范围);(3)、量筒中至少放入几个小球时有水溢出?21. 如图,在▱ABCD中,AE=CF,M、N分别是BE、DF的中点,试说明四边形MFNE是平行四边形. 22. 已知点A(a,3),B(b,6),C(5,c),AC⊥x轴,BC⊥y轴,且点B在第二象限的角平分线上.
22. 已知点A(a,3),B(b,6),C(5,c),AC⊥x轴,BC⊥y轴,且点B在第二象限的角平分线上. (1)、求出A,B,C三点的坐标.(2)、求△ABC的面积.23. 某市米厂接到加工大米任务,要求5天内加工完大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量与甲车间加工时间x(天)之间的关系如图1所示;未加工大米与甲车间加工时间x(天)之间的关系如图2所示,请结合图像回答下列问题
(1)、求出A,B,C三点的坐标.(2)、求△ABC的面积.23. 某市米厂接到加工大米任务,要求5天内加工完大米.米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止,设甲、乙两车间各自加工大米数量与甲车间加工时间x(天)之间的关系如图1所示;未加工大米与甲车间加工时间x(天)之间的关系如图2所示,请结合图像回答下列问题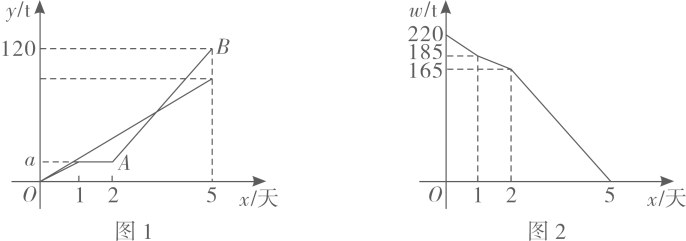 (1)、甲车间每天加工大米;a=;(2)、直接写出乙车间维修设备后,乙车间加工大米数量与x(天)之间的函数关系式,并指出自变量的取值范围.24. 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题.
(1)、甲车间每天加工大米;a=;(2)、直接写出乙车间维修设备后,乙车间加工大米数量与x(天)之间的函数关系式,并指出自变量的取值范围.24. 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,图(1)和图(2)是他通过采集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题. (1)、该班共有名学生;(2)、在图(1)中,将表示“步行”的部分补充完整;(3)、扇形图中表示骑车部分所占扇形的圆心角是 .(4)、如果小明所在年级共计800人,请你根据样本数据,估计一下该年级步行上学的学生人数是多少?
(1)、该班共有名学生;(2)、在图(1)中,将表示“步行”的部分补充完整;(3)、扇形图中表示骑车部分所占扇形的圆心角是 .(4)、如果小明所在年级共计800人,请你根据样本数据,估计一下该年级步行上学的学生人数是多少?