河北省唐山市迁安市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 如图,利用平面直角坐标系画出的正方形网格中,若A(﹣1,2),B(0,1),则点C的坐标为( )
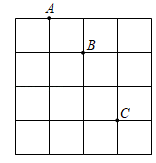 A、(1,﹣2) B、(1,﹣1) C、(2,1) D、(2,﹣1)2. 甲、乙两地去年12月前5天的日平均气温如图所示,则两地温差最大的是( )
A、(1,﹣2) B、(1,﹣1) C、(2,1) D、(2,﹣1)2. 甲、乙两地去年12月前5天的日平均气温如图所示,则两地温差最大的是( )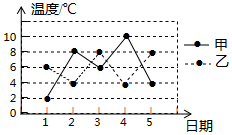 A、12月1日 B、12月2日 C、12月4日 D、12月5日3. 一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )A、6 B、8 C、12 D、164. 如图,在平面直角坐标系中,点P(﹣3,5)关于原点对称点的坐标(m,n),则m+n=( )
A、12月1日 B、12月2日 C、12月4日 D、12月5日3. 一个正多边形的边长为2,它的内角和是外角和的3倍,则这个多边形的周长是( )A、6 B、8 C、12 D、164. 如图,在平面直角坐标系中,点P(﹣3,5)关于原点对称点的坐标(m,n),则m+n=( )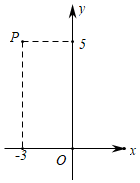 A、﹣2 B、﹣8 C、2 D、85. 某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )A、实际问题→收集数据→表示数据→整理数据→统计分析合理决策 B、实际问题→表示数据→收集数据→整理数据→统计分析合理决策 C、实际问题→收集数据→整理数据→表示数据→统计分析合理决策 D、实际问题→整理数据→收集数据→表示数据→统计分析合理决策6. 函数y= 中,自变量x的取值范围是( )A、x>0 B、x>1 C、x>0且x≠1 D、x≥0且x≠17. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x的一元一次不等式ax+b>kx的解集是( )
A、﹣2 B、﹣8 C、2 D、85. 某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )A、实际问题→收集数据→表示数据→整理数据→统计分析合理决策 B、实际问题→表示数据→收集数据→整理数据→统计分析合理决策 C、实际问题→收集数据→整理数据→表示数据→统计分析合理决策 D、实际问题→整理数据→收集数据→表示数据→统计分析合理决策6. 函数y= 中,自变量x的取值范围是( )A、x>0 B、x>1 C、x>0且x≠1 D、x≥0且x≠17. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x的一元一次不等式ax+b>kx的解集是( ) A、x<0 B、x>0 C、x>﹣3 D、x<﹣38. 若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是( )A、﹣9 B、﹣3 C、3 D、﹣3或39. 图1是装满了液体的高脚杯(数据如图),用去部分液体后,放在水平的桌面上如图2所示,此时液面AB=( )
A、x<0 B、x>0 C、x>﹣3 D、x<﹣38. 若正比例函数y=kx的图象经过点A(k,9),且经过第一、三象限,则k的值是( )A、﹣9 B、﹣3 C、3 D、﹣3或39. 图1是装满了液体的高脚杯(数据如图),用去部分液体后,放在水平的桌面上如图2所示,此时液面AB=( )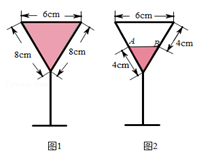 A、4cm B、3cm C、2cm D、1cm10. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )A、
A、4cm B、3cm C、2cm D、1cm10. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )A、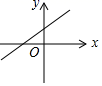 B、
B、 C、
C、 D、
D、 11. 关于函数y=﹣x﹣2的图象,有如下说法:
11. 关于函数y=﹣x﹣2的图象,有如下说法:①图象过点(0,﹣2)
②图象与x轴的交点是(﹣2,0)
③由图象可知y随x的增大而增大
④图象不经过第一象限
⑤图象是与y=﹣x+2平行的直线,
其中正确说法有( )
A、5个 B、4个 C、3个 D、2个12. 某天,小明走路去学校,开始他以较慢的速度匀速前进,然后他越走越快走了一段时间,最后他以较快的速度匀速前进达到学校.小明走路的速度v(米/分钟)是时间t(分钟)的函数,能符合题意反映这一函数关系的大致图像是( )A、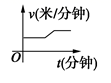 B、
B、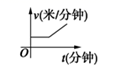 C、
C、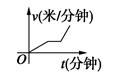 D、
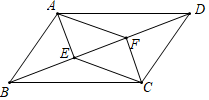
D、 13. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )
13. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )甲:只需要满足BE=DF
乙:只需要满足AE=CF
丙:只需要满足AE∥CF
 A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是14. 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )
A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是14. 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( ) A、7cm B、8.5cm C、9cm D、10cm15. 小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图1及条形图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中 “( )”应填的颜色是( )
A、7cm B、8.5cm C、9cm D、10cm15. 小明调查了本班每位同学最喜欢的颜色,并绘制了不完整的扇形图1及条形图2(柱的高度从高到低排列).条形图不小心被撕了一块,图2中 “( )”应填的颜色是( )
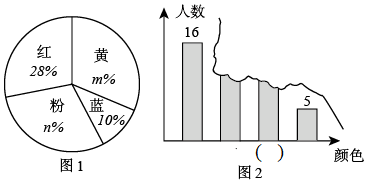 A、蓝 B、粉 C、黄 D、红16. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )
A、蓝 B、粉 C、黄 D、红16. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为( )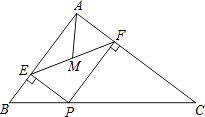 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 下表是某商店出售货物时其数量x(个)与售价y(元)的对应关系表:
数量x(个)
1
2
3
4
5
售价y(元)
8+0.2
16+0.2
24+0.2
32+0.2
40+0.2
根据表中提供的信息可知y与x之间的关系式是 .
18. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . 19. 如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的线路移动.
19. 如图,在矩形OABC中,O为平面直角坐标系的原点,点A的坐标为(a,0),点C的坐标为(0,b),且a、b满足+|b﹣6|=0,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O→C→B→A→O的线路移动. (1)、点B的坐标为 .(2)、当点P移动4秒时,请写出点P的坐标 .(3)、当点P移动2026秒时,请写出点P的坐标 .
(1)、点B的坐标为 .(2)、当点P移动4秒时,请写出点P的坐标 .(3)、当点P移动2026秒时,请写出点P的坐标 .三、解答题
-
20.(1)、某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度已知无人机在上升和下降过程中速度相同,设无人机的飞行高度M(米)与操控无人机的时间x(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:

①在上升或下降过程中,无人机的速度是米/分;
②图中a表示的数是 , b表示的数是;
③无人机在60米高的上空停留的时间是分钟;
(2)、已知平面直角坐标系中有一点P(2m+1,m﹣3).①若点P在第四象限,求m的取值范围;
②当点P到y轴的距离为3时,求点P的坐标 .
21. 体弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的图表,解答问题.组别
分数段
频数
频率
一
50.5~60.5
16
0.08
二
60.5~70.5
30
a
三
70.5~80.5
50
0.25
四
80.5~90.5
b
0.40
五
90.5~100.5
c
 (1)、本次抽样调查的样本容量为 , 表中a= , b= , c=补全频数分布直方图;(2)、若把各组的频率绘制成扇形统计图,则第三组对应的扇形圆心角是;(3)、若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?22. 如图,△ABC中,AB=AC,D、F分别为BC、AC的中点,连接DF并延长到点E,使DF=FE,连接AE、AD、CE.
(1)、本次抽样调查的样本容量为 , 表中a= , b= , c=补全频数分布直方图;(2)、若把各组的频率绘制成扇形统计图,则第三组对应的扇形圆心角是;(3)、若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?22. 如图,△ABC中,AB=AC,D、F分别为BC、AC的中点,连接DF并延长到点E,使DF=FE,连接AE、AD、CE. (1)、求证:四边形AECD是矩形.(2)、当△ABC满足什么条件时,四边形AECD是正方形,并说明理由.23. 某学校欲购置一批标价为4800元的某种型号电脑,需求数量在6至15台之间.经与两个专卖店商谈,优惠方法如下:
(1)、求证:四边形AECD是矩形.(2)、当△ABC满足什么条件时,四边形AECD是正方形,并说明理由.23. 某学校欲购置一批标价为4800元的某种型号电脑,需求数量在6至15台之间.经与两个专卖店商谈,优惠方法如下:甲店:购买电脑打八折;
乙店:先赠一台电脑,其余电脑打九折优惠.
设学校欲购置x台电脑,甲店购买费用为y甲(元),乙店购买费用为y乙(元).
(1)、分别写出购买费用y甲、y乙与所购电脑x(台)之间的函数关系式;(2)、对x的取值情况进行分析,说明这所学校购买哪家电脑更合算?24. 已知:如图,在▱ABCD中,对角线AC、BD相交于点O,点G、H分别是AD、BC的中点,点E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F. (1)、求证:四边形GEHF是平行四边形;(2)、若四边形GEHF是菱形.
(1)、求证:四边形GEHF是平行四边形;(2)、若四边形GEHF是菱形.①线段AB和BD有何位置关系?请说明理由.
②若AB=2,BD=2AB时,求四边形GEHF的面积.
25. 甲、乙两人相约春游去登山,山高300米,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: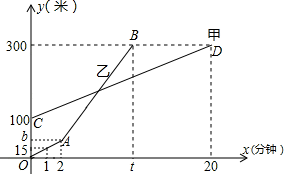 (1)、b=m;(2)、若乙提速后,乙登山的速度是甲登山速度3倍;
(1)、b=m;(2)、若乙提速后,乙登山的速度是甲登山速度3倍;①则t= ▲ min;
②登山多长时间乙追上了甲,求出此时x的值;
③在上山过程中,先到达山顶的一人原地休息等待另一人,当甲、乙两人距地面高度差为50m时,求出此时x的值.