河北省唐山市古冶区2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 下列根式中是最简二次根式的是( )A、 B、 C、 D、2. 若式子有意义,则x的取值范围是( )A、 B、 C、 D、3. 下列四组数据中,不能作为直角三角形三边长的是( )A、5,12,13 B、1,2,3 C、6,8,10 D、3,4,54. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、3 C、﹣ D、﹣35. 若平行四边形其中两个内角的度数之比为 , 则其中较小的内角是A、 B、 C、 D、6. 下图均由正六边形与两条对角线所组成,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 7. 两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学成绩哪一位更稳定,通常还需要比较他们成绩的( )A、众数 B、中位数 C、方差 D、以上都不对8. 如图,已知直线 与 相交于点 (2, ),若 ,则 的取值范围是( )
7. 两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学成绩哪一位更稳定,通常还需要比较他们成绩的( )A、众数 B、中位数 C、方差 D、以上都不对8. 如图,已知直线 与 相交于点 (2, ),若 ,则 的取值范围是( ) A、 B、 C、 D、9. 如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A、 B、 C、 D、9. 如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )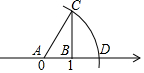 A、 B、 C、 D、10. 某厂质检部将甲,乙两人第一周每天生产合格产品的个数整理成两组数据,如表:根据数据表,说法正确的是( )
A、 B、 C、 D、10. 某厂质检部将甲,乙两人第一周每天生产合格产品的个数整理成两组数据,如表:根据数据表,说法正确的是( )甲
2
6
7
7
8
乙
2
3
4
8
8
A、甲、乙的众数相同 B、甲、乙的中位数相同 C、甲的平均数小于乙的平均数 D、甲的方差小于乙的方差11. 如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节 间的距离,若 间的距离调节到60 ,菱形的边长 ,则 的度数是( )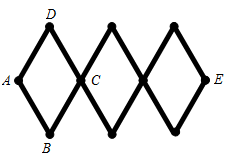 A、 B、 C、 D、12. 如图,正方形的边长为 , 正方形的边长为 , 若正方形绕点C旋转,则点F到点A的距离最小值为( )
A、 B、 C、 D、12. 如图,正方形的边长为 , 正方形的边长为 , 若正方形绕点C旋转,则点F到点A的距离最小值为( ) A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
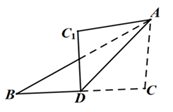
13. 在平行四边形ABCD中,AB=5,则CD= .14. 一次函数y=2x+4的图象与y轴交点的坐标是 .15. 若一组数据3,x,4,2的众数和中位数相等,则x的值为 .16. 点关于原点对称的点的坐标是 .17. 如图, 为 的 边上的中线,沿 将 折叠,点 的对应点为 ,已知 ,则点 与点 之间的距离是
 18. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是
18. 如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2,将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是
三、解答题
-
19. 如图所示,的顶点在的网格中的格点上,

( 1 )画出绕点A逆时针旋转得到的;
( 2 )画出绕点A顺时针旋转得到的
20.(1)、设中, , , , 求的长.(2)、已知中, , , , ().求证:是直角三角形.21. 已知y是x的一次函数,且当 时, ;当 时, .(1)、求这个一次函数的解析式;(2)、当 时,求函数y的值;(3)、当 时,求自变量x的取值范围.22. 某学校从甲、乙两位班主任中选拔一位参加教育局班主任技能大赛,选拔内容包括案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两位班主任的成绩并制成了如图所示的统计, (1)、乙班主任三个项目的成绩的中位数是 .(2)、若按照案例分析:班会设计:才艺展示按照的权重进行计算,选拔总分最高的一位班主任参加比赛,请你确定哪位班主任将获得参赛资格,说明理由.23. 如图,平行四边形ABCD中,∠C=60°, BC=6, DC=3, E是AD 中点, F是DC边上任意一点, M, N分别为EF和BF中点.求MN的长.
(1)、乙班主任三个项目的成绩的中位数是 .(2)、若按照案例分析:班会设计:才艺展示按照的权重进行计算,选拔总分最高的一位班主任参加比赛,请你确定哪位班主任将获得参赛资格,说明理由.23. 如图,平行四边形ABCD中,∠C=60°, BC=6, DC=3, E是AD 中点, F是DC边上任意一点, M, N分别为EF和BF中点.求MN的长. 24. 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示.
24. 甲、乙两车间同时开始加工一批服装.从开始加工到加工完这批服装甲车间工作了9小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为y(件).甲车间加工的时间为x(时),y与x之间的函数图象如图所示. (1)、甲车间每小时加工服装件数为件;这批服装的总件数为件.(2)、求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)、求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.25. 如图,四边形中,对角线与交于点O, .
(1)、甲车间每小时加工服装件数为件;这批服装的总件数为件.(2)、求乙车间维修设备后,乙车间加工服装数量y与x之间的函数关系式;(3)、求甲、乙两车间共同加工完1000件服装时甲车间所用的时间.25. 如图,四边形中,对角线与交于点O, . (1)、求证:四边形是正方形;(2)、若H是边上一点(H与A,B不重合),连接 , 将线段绕点H顺时针旋转90°,得到线段 , 过点E分别作及延长线的垂线,垂足分别为F、G,求证:四边形是正方形.
(1)、求证:四边形是正方形;(2)、若H是边上一点(H与A,B不重合),连接 , 将线段绕点H顺时针旋转90°,得到线段 , 过点E分别作及延长线的垂线,垂足分别为F、G,求证:四边形是正方形.