河北省邯郸市永年区2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 下列各图能表示 是 的函数的是( )A、
 B、
B、 C、
C、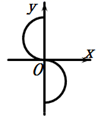 D、
D、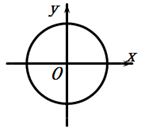 2. 下列调查中,适合用抽样调查的是( )A、防疫期间对进入校园的人员进行体温检测 B、对乘坐高铁的乘客进行安检 C、调查一批防疫口罩的质量情况 D、对新研发导弹的零部件进行检查3. 如图,学校(记作A)在蕾蕾家(记作B)南偏西25°的方向上,且与蕾蕾家的距离是4km,若∠ABC=90°,且AB=BC,则超市(记作C)在蕾蕾家的( )
2. 下列调查中,适合用抽样调查的是( )A、防疫期间对进入校园的人员进行体温检测 B、对乘坐高铁的乘客进行安检 C、调查一批防疫口罩的质量情况 D、对新研发导弹的零部件进行检查3. 如图,学校(记作A)在蕾蕾家(记作B)南偏西25°的方向上,且与蕾蕾家的距离是4km,若∠ABC=90°,且AB=BC,则超市(记作C)在蕾蕾家的( ) A、南偏东65°的方向上,相距4km B、南偏东55°的方向上,相距4km C、北偏东55°的方向上,相距4km D、北偏东65°的方向上,相距4km4. 如果一个正多边形的每一个外角都是45°,那么这个正多边形的内角和为( )A、360° B、720° C、1080° D、1440°5. 已知一次函数 , 且y随x的增大而增大,则此图像不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )A、抽取的50名男生是总体 B、抽取的50名男生是样本 C、每一名男生的体重是个体 D、样本容量是50名7. 如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的 , 那么所得的图形与原图形相比( )A、形状不变,图形缩小为原来的一半 B、形状不变,图形放大为原来的2倍 C、整个图形被横向压缩为原来的一半 D、整个图形被纵向压缩为原来的一半8. 如图,直线与直线相交于点 , 则关于x,y的方程组的解为( )
A、南偏东65°的方向上,相距4km B、南偏东55°的方向上,相距4km C、北偏东55°的方向上,相距4km D、北偏东65°的方向上,相距4km4. 如果一个正多边形的每一个外角都是45°,那么这个正多边形的内角和为( )A、360° B、720° C、1080° D、1440°5. 已知一次函数 , 且y随x的增大而增大,则此图像不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 为了了解某市初一男生的体重,有关部门从初一年级498名男生中抽取50名男生进行测量,下列说法正确的是( )A、抽取的50名男生是总体 B、抽取的50名男生是样本 C、每一名男生的体重是个体 D、样本容量是50名7. 如果一个图形上各点的横坐标保持不变,而纵坐标分别都变化为原来的 , 那么所得的图形与原图形相比( )A、形状不变,图形缩小为原来的一半 B、形状不变,图形放大为原来的2倍 C、整个图形被横向压缩为原来的一半 D、整个图形被纵向压缩为原来的一半8. 如图,直线与直线相交于点 , 则关于x,y的方程组的解为( ) A、 B、 C、 D、9. 如图,平行四边形的周长为20,对角线、交于点O,E为的中点, , 则的周长为( )
A、 B、 C、 D、9. 如图,平行四边形的周长为20,对角线、交于点O,E为的中点, , 则的周长为( ) A、5 B、8 C、10 D、1210. 2020年以来,中美贸易摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性,进出口保持稳中提质的发展势头,如图是某省近五年进出口情况统计图,下列描述不正确的是( )
A、5 B、8 C、10 D、1210. 2020年以来,中美贸易摩擦影响持续显现,我国对外贸易仍然表现出很强的韧性,进出口保持稳中提质的发展势头,如图是某省近五年进出口情况统计图,下列描述不正确的是( ) A、这五年,2015年出口额最少 B、这五年,出口总额比进口总额多 C、这五年,出口增速前四年逐年下降 D、这五年,2019年进口增速最快11. 如图,明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,若棋盘中心的圆形棋子位置用(-1,1)表示,乐乐将第4枚方形棋子放入棋盘后,所有棋子构成轴对称图形,则乐乐放方形棋子的位置可能是( )
A、这五年,2015年出口额最少 B、这五年,出口总额比进口总额多 C、这五年,出口增速前四年逐年下降 D、这五年,2019年进口增速最快11. 如图,明明和乐乐下棋,明明执圆形棋子,乐乐执方形棋子,若棋盘中心的圆形棋子位置用(-1,1)表示,乐乐将第4枚方形棋子放入棋盘后,所有棋子构成轴对称图形,则乐乐放方形棋子的位置可能是( ) A、 B、 C、 D、12. 平面立角坐标系中,点 , , 经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( )A、(0,-1) B、(-1,-2) C、(-2,-1) D、(2,3)13. 如图,在正方形中,与相交于点O.嘉嘉作 , , 在正方形外, , 交于点P;淇淇作 , , 在正方形外, , 交于点P,两人的作法中,能使四边形是正方形的是( )
A、 B、 C、 D、12. 平面立角坐标系中,点 , , 经过点A的直线轴,点C是直线a上的一个动点,当线段BC的长度最短时,点C的坐标为( )A、(0,-1) B、(-1,-2) C、(-2,-1) D、(2,3)13. 如图,在正方形中,与相交于点O.嘉嘉作 , , 在正方形外, , 交于点P;淇淇作 , , 在正方形外, , 交于点P,两人的作法中,能使四边形是正方形的是( ) A、只有嘉嘉 B、只有淇淇 C、嘉嘉和淇淇 D、以上均不符合题意14. 如图,在平面直角坐标系中,直线 : 与x轴、y轴分别交于点A和点B , 直线 经过坐标原点,且 ,垂足为C , 则点C到y轴的距离为( )
A、只有嘉嘉 B、只有淇淇 C、嘉嘉和淇淇 D、以上均不符合题意14. 如图,在平面直角坐标系中,直线 : 与x轴、y轴分别交于点A和点B , 直线 经过坐标原点,且 ,垂足为C , 则点C到y轴的距离为( ) A、1 B、2 C、3 D、415. 一列慢车从甲地驶往乙地,一列快车从乙地驶往甲地,慢车的速度为100千米/小时,快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离 (千米)与慢车行驶时间 (小时)之间函数图象的是( )A、
A、1 B、2 C、3 D、415. 一列慢车从甲地驶往乙地,一列快车从乙地驶往甲地,慢车的速度为100千米/小时,快车的速度为150千米/小时,甲、乙两地之间的距离为1000千米,两车同时出发,则图中折线大致表示两车之间的距离 (千米)与慢车行驶时间 (小时)之间函数图象的是( )A、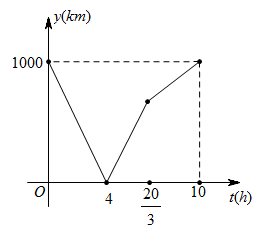 B、
B、 C、
C、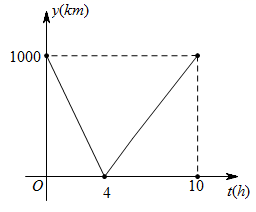 D、
D、 16. 如图,分别以的斜边 , 直角边为边向外作等边和 , F为的中点, , 相交于点G,若 , 下列结论:①;②四边形为平行四边形;③;④ , 其中正确结论的序号是( )
16. 如图,分别以的斜边 , 直角边为边向外作等边和 , F为的中点, , 相交于点G,若 , 下列结论:①;②四边形为平行四边形;③;④ , 其中正确结论的序号是( ) A、①②④ B、①③ C、②③④ D、①②③④
A、①②④ B、①③ C、②③④ D、①②③④二、填空题
-
17. 如图,在平面直角坐标系中,已知点 , 平移线段 , 使点M落在点处,则点N对应的点的坐标为 .
 18. 近年来,计算步数的软件悄然兴起,每天监测自己的行走步数已成为当代人的一种习惯.某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.根据统计图,得出下面四个结论,请把正确结论的序号写在横线上 .
18. 近年来,计算步数的软件悄然兴起,每天监测自己的行走步数已成为当代人的一种习惯.某机构调查了某小区部分居民当天行走的步数(单位:千步),并将数据整理绘制成如下不完整的频数直方图和扇形统计图.根据统计图,得出下面四个结论,请把正确结论的序号写在横线上 .

①此次一共调查了200位小区居民
②行走步数为8~12千步的人数超过调查总人数的一半
③行走步数为12~16千步的人数为40人
④扇形图中,表示行走步数为4~8千步的扇形圆心角是90
19. 如图, , 其中 , O为中点,过点O分别交、于点E、F,连接、 , 有以下四个结论:①四边形为平行四边形;②当时,四边形为矩形;③当时,四边形为菱形;④四边形不可能为正方形.其中错误的结论是 . (填写序号) 20. 如图1,在长方形中,动点P从点A出发,沿方向运动至D点处停止,设点P出发时的速度为每秒 , a秒后点P改变速度,以每秒向点D运动,直到停止.图2是的面积与时间的图像,则b的值是 .
20. 如图1,在长方形中,动点P从点A出发,沿方向运动至D点处停止,设点P出发时的速度为每秒 , a秒后点P改变速度,以每秒向点D运动,直到停止.图2是的面积与时间的图像,则b的值是 .
三、解答题
-
21. 已知点 , 请分别根据下列条件,求出a的值并写出点A的坐标.(1)、点A在x轴上;(2)、点A与点关于y轴对称;(3)、点A到两坐标轴的距离相等.22. 为了传承中华民族优秀传统文化,石家庄市某中学组织了一次“中华民族优秀传统文化知识竞赛”活动,比赛后整理参赛学生的成绩,将参赛学生的成绩分为A、B、C、D四个等级,并制作了如下的统计表和统计图,但都不完整,请你根据统计图、表解答下列问题:

等级
频数(人)
频率
A
30
10%
B
90
30%
C
m
40%
D
60
n
(1)、在表中,m= ;n= ;(2)、补全频数直方图;(3)、扇形统计图中圆心角β的度数是;(4)、请你估计全市八年级2万名考生中,成绩评为“B”级及以上的学生大约有多少名?23. 已知一次函数的图像为 , 函数的图像为 . 按要求完成下列问题:(1)、求直线与y轴交点A的坐标;求直线与y轴的交点B的坐标;(2)、求一次函数的图象与的图象的交点P的坐标;(3)、求由三点P、A、B围成的三角形的面积.24. 已知,如图,在中,对角线与相交于点O,过点C作的平行线,过点D作的平行线,两线相交于点P. (1)、当四边形是矩形时,证明四边形是菱形;(2)、当四边形是菱形时,且 . 求点O到点P的距离.25. 某商场计划采购 , 两种不同型号的电视机共50台,已知 型电视机进价1500元,售价2000元; 型电视机进价为2400元,售价3000元.(1)、设该商场购进 型电视机 台,请写出全部售出后该商店获利 与 之间函数表达式.(2)、若该商场采购两种电视机的总费用不超过108300元,全部售出所获利润不低于28500元,请设计出所有采购方案,并求出使商场获得最大利润的采购方案及最大利润.26. 如图,在边长为6的正方形中,点M为对角线上任意一点(可与B,D重合),连接 , 将线段绕点A逆时针旋转得到线段 , 连接 , , 设 .
(1)、当四边形是矩形时,证明四边形是菱形;(2)、当四边形是菱形时,且 . 求点O到点P的距离.25. 某商场计划采购 , 两种不同型号的电视机共50台,已知 型电视机进价1500元,售价2000元; 型电视机进价为2400元,售价3000元.(1)、设该商场购进 型电视机 台,请写出全部售出后该商店获利 与 之间函数表达式.(2)、若该商场采购两种电视机的总费用不超过108300元,全部售出所获利润不低于28500元,请设计出所有采购方案,并求出使商场获得最大利润的采购方案及最大利润.26. 如图,在边长为6的正方形中,点M为对角线上任意一点(可与B,D重合),连接 , 将线段绕点A逆时针旋转得到线段 , 连接 , , 设 . (1)、求证:;(2)、当时,求的长;(3)、嘉淇同学在完成(1)后有个想法:“与也会存在全等的情况”,请判断嘉淇的想法是否正确,若正确,请直接写出与全等时x的值;若不正确,请说明理由.
(1)、求证:;(2)、当时,求的长;(3)、嘉淇同学在完成(1)后有个想法:“与也会存在全等的情况”,请判断嘉淇的想法是否正确,若正确,请直接写出与全等时x的值;若不正确,请说明理由.