河北省邯郸市临漳县2020-2021学年八年级下学期期末考试数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 如图,在等边三角形 中, , 分别是 , 的中点,点 是线段 上的一个动点,当 的周长最小时, 点的位置在( )
 A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处2. 已知a>b>0,下列结论不正确的是( )A、 B、 C、 D、3. 如图,直线与的交点坐标为 , 则使的x的取值范围为( )
A、 点处 B、 点处 C、 的中点处 D、 三条高的交点处2. 已知a>b>0,下列结论不正确的是( )A、 B、 C、 D、3. 如图,直线与的交点坐标为 , 则使的x的取值范围为( ) A、 B、 C、 D、4. 将下列多项式分解因式,结果中不含因式x﹣1的是( )A、x2﹣1 B、x(x﹣2)+(2﹣x) C、x2﹣2x+1 D、x2+2x+15. 已知 是分式方程 的解,那么实数 的值为( )A、3 B、4 C、5 D、66. 已知坐标平面内一点A(2,1),O为原点,B是x轴上一个动点,如果以点B,O,A为顶点的三角形是等腰三角形,那么符合条件的动点B的个数为( )A、2个 B、3个 C、4个 D、5个7. 若a是不等式2x-1>5的解,但b不是不等式2x-1>5的解,则下列选项中,正确的是( )A、a<b B、a>b C、a≤b D、a≥b8. 关于x的不等式组有解,则a的值不可能是( )A、 B、 C、 D、9. 下列因式分解正确的有几个( )
A、 B、 C、 D、4. 将下列多项式分解因式,结果中不含因式x﹣1的是( )A、x2﹣1 B、x(x﹣2)+(2﹣x) C、x2﹣2x+1 D、x2+2x+15. 已知 是分式方程 的解,那么实数 的值为( )A、3 B、4 C、5 D、66. 已知坐标平面内一点A(2,1),O为原点,B是x轴上一个动点,如果以点B,O,A为顶点的三角形是等腰三角形,那么符合条件的动点B的个数为( )A、2个 B、3个 C、4个 D、5个7. 若a是不等式2x-1>5的解,但b不是不等式2x-1>5的解,则下列选项中,正确的是( )A、a<b B、a>b C、a≤b D、a≥b8. 关于x的不等式组有解,则a的值不可能是( )A、 B、 C、 D、9. 下列因式分解正确的有几个( )⑴;⑵;⑶;⑷;⑸+y+=
A、1 B、2 C、3 D、410. 如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )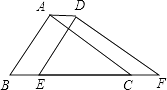 A、6 B、8 C、10 D、1211. 下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是( )A、
A、6 B、8 C、10 D、1211. 下列各图中,既可经过平移,又可经过旋转,由图形①得到图形②的是( )A、 B、
B、 C、
C、 D、
D、 12. 如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
12. 如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( ) A、(1.5,1.5) B、(1,0) C、(1,-1) D、(1.5,-0.5)13. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、514. 不等式的解集在数轴上表示为( )A、
A、(1.5,1.5) B、(1,0) C、(1,-1) D、(1.5,-0.5)13. 关于x的分式方程 +5= 有增根,则m的值为( )A、1 B、3 C、4 D、514. 不等式的解集在数轴上表示为( )A、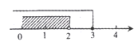 B、
B、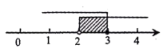 C、
C、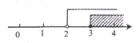 D、
D、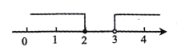 15.
15.运行程序如图所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作,如果程序操作进行了三次才停止,那么x的取值范围是( )
 A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤2316. 一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是( )
A、x≥11 B、11≤x<23 C、11<x≤23 D、x≤2316. 一个数学游戏,正六边形被平均分为6格(其中1格涂有阴影),规则如下:若第一个正六边形下面标的数字为a(a为正整数),则先绕正六边形的中心顺时针旋转a格;再沿某条边所在的直线l翻折,得到第二个图形。例如:若第一个正六边形下面标的数字为2,如图,则先绕其中心顺时针旋转2格;再沿直线l翻折,得到第二个图形。若第一个正六边形下面标的数字为4,如图,按照游戏规则,得到第二个图形应是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
17. 一个多边形的内角和是外角和的3倍,则它是边形.18. 计算的结果等于 .19. 如图,菱形中, , , 其周长为 .
 20. 如图,在等边中,于点D,若 , , E为的中点,P为上一点,的最小值为 .
20. 如图,在等边中,于点D,若 , , E为的中点,P为上一点,的最小值为 .
三、解答题
-
21. 若x+y=3,且(x+2)(y+2)=12.(1)、求xy的值;(2)、求x2+3xy+y2的值.22. 解方程(1)、+=1(2)、+1=23. 定义新运算:对于任意实数a,b,都有a⊕b=a(a-b)+1,等式右边是通常的加法、减法及乘法运算,比如: 2⊕5=2´(2-5)+1=2´(-3)+1=-6+1=-5.
 (1)、求(-2)⊕3的值(2)、若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.24. 已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止).
(1)、求(-2)⊕3的值(2)、若3⊕x的值小于13,求x的取值范围,并在图示的数轴上表示出来.24. 已知,△ABC是等边三角形,将直角三角板DEF如图放置,其中∠F=30°,让△ABC在直角三角板的边EF上向右平移(点C与点F重合时停止). (1)、如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC .(2)、在△ABC平移过程中,AB , AC分别与三角板斜边的交点为G、H , 如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.25. 如图,平行四边形 的周长是 ,对角线 与 交于点 , , 是 中点, 的周长比 的周长多 .
(1)、如图1,当点B与点E重合时,点A恰好落在直角三角板的斜边DF上,证明:EF=2BC .(2)、在△ABC平移过程中,AB , AC分别与三角板斜边的交点为G、H , 如图2,线段EB=AH是否始终成立?如果成立,请证明;如果不成立,请说明理由.25. 如图,平行四边形 的周长是 ,对角线 与 交于点 , , 是 中点, 的周长比 的周长多 . (1)、求边 , 的长;(2)、求 的长度;(3)、求平行四边形 的面积.26. 李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:
(1)、求边 , 的长;(2)、求 的长度;(3)、求平行四边形 的面积.26. 李辉到服装专卖店去做社会调查,了解到商店为了激励营业员的工作积极性实行了“月总收入=基本工资+计件奖金”的方法,并获得了如下信息:营业员
嘉琪
嘉善
月销售件数/件
400
300
月总收入/元
7800
6600
假设月销售件数为x件,月总收入为y元,销售每件奖励a元,营业员月基本工资为b元.
(1)、求a、b的值.(2)、若营业员嘉善某月总收入不低于4200元,那么嘉善当月至少要卖多少件衣服?