河北省邯郸市邯山区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 当x是怎样实数时，式子 $\sqrt{x - 1}$ 在实数范围内有意义（）

A、 $x < 1$ B、 $x \leq 1$ C、 $x > 1$ D、 $x \geq 1$

查看试题解析
2. 计算（2 $\sqrt{5} - 2 \sqrt{3}$ ）（ $\sqrt{12} + \sqrt{20}$ ）的结果是（）

A、4 B、8 C、16 D、32

查看试题解析
3. 如图，下列四组条件中.不能判定四边形ABCD是平行四边形的是（　　）

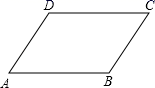A、AB＝DC，AD＝BC B、AB∥DC，AD∥BC C、AB∥DC，AD＝BC D、AB∥DC，AB＝DC

查看试题解析
4. 某市在一次空气污染指数抽查中，收集到10天的数据如下：61，75，70，56，81，91，92，91，75，81，该组数据的中位数是（）

A、78 B、81 C、91 D、77.3

查看试题解析
5. 实数a，b 在数轴上的位置如图所示，则化简 $\sqrt{a^{2}}$ - $\sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$ 的结果是（）

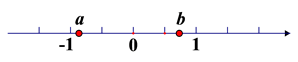A、0 B、- 2 a C、2（b−a） D、- 2b

查看试题解析
6. 如图，一个函数的图象由射线BA、线段BC、射线CD组成，其中点A（﹣2，2），B（1，3），C（2，1），D（6，5），则此函数（　　）

A、当x＜2时，y随x的增大而增大 B、当x＜2时，y随x的增大而减小 C、当x＞2时，y随x的增大而增大 D、当x＞2时，y随x的增大而减小

查看试题解析
7. 如图，一棵高为16m的大树被台风刮数断，若树在地面6m处折断，则树顶端落在离树底部（）处

A、5m B、7m C、8m D、10m

查看试题解析
8. 如图是小颖前三次购买苹果单价的统计图，第四次又买的苹果单价是a元/千克，发现这四个单价的中位数恰好也是众数，则a=（）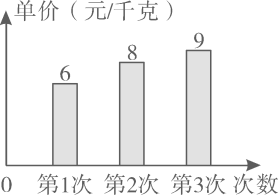

A、9 B、8 C、7 D、6

查看试题解析
9. 一次函数y=kx+b中，y随x的增大而减小，b＜0，则这个函数的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $A B = 1$ ， $B C = 1$ ， $C D = 2$ ， $D A = \sqrt{6}$ ，且 $∠ A B C = 9 0^{∘}$ ，则四边形 $A B C D$ 的面积是（）

A、 $2$ B、 $\frac{1}{2} + \sqrt{2}$ C、 $1 + \sqrt{2}$ D、 $\frac{1 + \sqrt{2}}{2}$

查看试题解析
11. 如图．在菱形ABCD中，对角线AC，BD交于点O，下列说法不正确的是（　　）

A、AB∥DC B、AC=BD C、AC⊥BD D、OA=OC

查看试题解析
12. 12位参加歌唱比赛的同学的成绩各不相同，按成绩取前6位进入决赛．如果小尹知道了自己的成绩后，要判断自己能否进入决赛，他还要知道这12位同学成绩的（）

A、平均数 B、众数 C、方差 D、中位数

查看试题解析
13. 下列说法中，不正确的是（）

A、菱形的对角线互相垂直 B、对角线互相垂直的四边形是菱形 C、矩形的四个内角都相等 D、四个内角都相等的四边形是矩形

查看试题解析
14. 如图，在平面直角坐标系中，已知一次函数 $y = (k - 2) x - b$ 的图象大致如图所示，则下列结论正确的是（）

A、 $k > 2 ， b > 0$ B、 $k > 2 ， b < 0$ C、 $k < 2 ， b > 0$ D、 $k < 2 ， b < 0$

查看试题解析
15. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A、1，4，5 B、2，3，5 C、3，4，5 D、2，2，4

查看试题解析
16. 如图，在平面直角坐标系中，点 $A_{1} ， A_{2} ， A_{3} \dots$ ，都在x轴上，点 $B_{1} ， B_{2} ， B_{3} \dots$ 在直线 $y = x$ 上， $△ O A_{1} B_{1} ， △ B_{1} A_{1} A_{2} ， △ B_{2} A_{2} A_{3} ， △ B_{3} A_{3} A_{4} …$ ，都是等腰直角三角形，如果 $O A_{1} = 1$ ，则点 $B_{2018}$ 的坐标是（）

A、 $(2^{2018} ， 2^{2018})$ B、 $(2^{2017} ， 2^{2017})$ C、 $(2^{2016} ， 2^{2016})$ D、 $(2^{2015} ， 2^{2015})$

查看试题解析

二、填空题

17. 已知： $\sqrt{18} - \sqrt{2} = a \sqrt{2} - \sqrt{2} = b \sqrt{2}$ ，则 $a b =$ ．

查看试题解析
18. 若直角三角形两边分别是3和4，则第三边是．

查看试题解析
19. 国家规定“中小学生每天在校体育活动时间不低于 $1 h$ ”．为此，某市就“每天在校体育活动时间”的问题随机调查了辖区内320名初中生，根据调查结果绘制成的统计图（部分）如图所示，其中分组情况是：A组： $t < 0.5 h$ ；B组： $0.5 h \leq t < 1 h$ ；C组： $1 h \leq t < 1.5 h$ ；D组： $t \geq 1.5 h$ ，请根据上述信息解答下列问题：

(1)、C组的人数是；

(2)、本次调查数据的中位数落在组内；

(3)、若该市辖区内约有32000名初中学生，请你估计其中达到国家规定体育活动时间的人约有名．

查看试题解析

三、解答题

20. 计算：

(1)、 $2 \sqrt{3} \times \sqrt{6}$

(2)、 $(\sqrt{5} + 2)^{2} + (\sqrt{5} + 2) (\sqrt{5} - 2)$

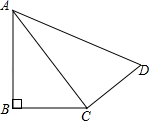
查看试题解析
21. 某中学八（1）班小明在综合实践课上剪了一个四边形ABCD，如图，连接AC，经测量AB＝12，BC＝9，CD＝8，AD＝17，∠B＝90°．求证：△ACD是直角三角形．

查看试题解析
22. 一辆汽车的邮箱中现有汽油 $50 L$ ，如果不再加油，那么邮箱中的油量y（单位：L）随行驶里程x（单位： $k m$ ）的增加而减少，平均耗油是为 $0.1 L / k m$ ．

(1)、写出表示y与x的函数关系式；并写出自变量x的取值范围；

(2)、汽车行驶 $200 k m$ 时，邮箱中还有多少汽油？

查看试题解析
23. 已知：如图，在 $Δ A B C$ 中，∠BAC=90°，DE、DF是 $Δ A B C$ 的中位线，连接EF、AD．
求证：EF=AD．

查看试题解析
24. 已知一次函数图象经过（-2，1）和（1，3）两点．

(1)、求这个一次函数的解析式；

(2)、当 $x = 3$ 时，求y的值．

查看试题解析
25. 某校党史识此赛的参赛选手名单已基本确定，最后还需要在小王和小李二人中挑选1人参加比赛，在最近五次选拔测试中，他们的成绩（单位：分）分别如下：
小王：70，80，100，95，80；
小李：75，95，85，85，85．
根据所给信息回答下列问题：

(1)、完成表格：
姓名
平均数（分）
中位数（分）
众数
方差
小王
85
80
120
小李
85
85

(2)、在这五次测试中，成绩比较稳定的队员是．

(3)、历届比赛表明，成绩达到85分以上（含85分）就很可能获奖；成绩达到95分以上（含95分）就很可能获得金牌那么，你认为选谁参加比赛比较合适？请说明你的理由．

查看试题解析
26. 如图，已知在▱ABCD中，对角线AC，BD交于点O，E是BD延长线上的点，且EA=EC．

(1)、求证：四边形ABCD是菱形；

(2)、若∠DAC=∠EAD+∠AED，求证：四边形ABCD是正方形．

查看试题解析

姓名	平均数（分）	中位数（分）	众数	方差
小王	85	80		120
小李	85		85