河北省承德市2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 为了解某学校七至九年级共3000名学生每天的体育锻炼时间,下列抽样调查的样本代表性较好的是( ).A、选择七年级一个班进行调查 B、选择八年级全体学生进行调查 C、先对全校学生按照1~3000进行编号,然后抽取学号是5的整数倍的学生进行调查 D、对九年级每个班按5%的比例用抽签的方法确定调查者2. 若实数a,b满足 , 则函数的图像可能是( ).A、
 B、
B、 C、
C、 D、
D、 3. 已知正比例函数 的图象经过点(1,-2),则正比例函数的解析式为( )A、 B、 C、 D、4. 如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )A、6 B、11 C、12 D、185. 已知A(x1 , y1),B(x2 , y2)是一次函数y=(2a﹣1)x﹣3图象上的两点,当x1<x2时,有y1>y2 , 则a的取值范围是( )A、a<2 B、a> C、a>2 D、a<6. 一家鞋店在一段时间内销售了某种女式鞋子38双,其中各种尺码的鞋子的销售量如下表:
3. 已知正比例函数 的图象经过点(1,-2),则正比例函数的解析式为( )A、 B、 C、 D、4. 如果一个正多边形的一个外角为30°,那么这个正多边形的边数是( )A、6 B、11 C、12 D、185. 已知A(x1 , y1),B(x2 , y2)是一次函数y=(2a﹣1)x﹣3图象上的两点,当x1<x2时,有y1>y2 , 则a的取值范围是( )A、a<2 B、a> C、a>2 D、a<6. 一家鞋店在一段时间内销售了某种女式鞋子38双,其中各种尺码的鞋子的销售量如下表:鞋的尺码
23
24
销售量/双
3
6
12
9
8
下列说法不正确的是( ).
A、频数最大的数据是 B、频数最小的数据是3 C、数据为24码的频数是9 D、数据为23码的频率约为7. 甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅拿尺子要他们帮忙检测一个窗框是否是矩形,他们各自做了如下检测,检测后,他们都说窗框是矩形,你认为最有说服力的是( )A、甲量的窗框两组对边分别相等 B、丙量的窗框的一组邻边相等 C、乙量的窗框的对角线相等 D、丁量的窗框的两组对边分别相等且两条对角线也相等8. 下列图形是中心对称图形但不是轴对称图形的是( )A、菱形 B、矩形 C、正三角形 D、平行四边形9. 菱形OABC在平面直角坐标系中的位置如图所示,若OA = 2,∠AOC = 45°,则B点的坐标是 A、(2 + , ) B、(2﹣ , ) C、(﹣2 + , ) D、(﹣2﹣ , )10. 如图,过正方形的顶点作直线 , 点、到直线的距离分别为和 , 则的长为( )
A、(2 + , ) B、(2﹣ , ) C、(﹣2 + , ) D、(﹣2﹣ , )10. 如图,过正方形的顶点作直线 , 点、到直线的距离分别为和 , 则的长为( ) A、 B、 C、 D、11. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )
A、 B、 C、 D、11. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,下列条件中,不能使四边形DBCE成为菱形的是( )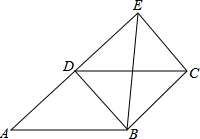 A、AB=BE B、BE⊥DC C、∠ABE=90° D、BE平分∠DBC12. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、
A、AB=BE B、BE⊥DC C、∠ABE=90° D、BE平分∠DBC12. 一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15km/h,水流速度为5km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )A、 B、
B、 C、
C、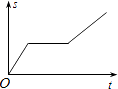 D、
D、 13. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两条弧在第二象限交于点P,若点P的坐标为(a,2b﹣1),则a,b的数量关系是( )
13. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两条弧在第二象限交于点P,若点P的坐标为(a,2b﹣1),则a,b的数量关系是( ) A、a=b B、a+2b=1 C、a﹣2b=1 D、a+2b=﹣114. 若直线与直线的交点在第一象限,则m的取值范围是( ).A、 B、 C、 D、15. 如图,在同一直线上,甲、乙两人分别从A,B两点同时向右出发,甲、乙均为匀速,图2表示两人之间的距离y(m)与所经过的时间t(s)之间的函数关系图象,若乙的速度为1.5m/s,则经过30s,甲自A点移动了( )
A、a=b B、a+2b=1 C、a﹣2b=1 D、a+2b=﹣114. 若直线与直线的交点在第一象限,则m的取值范围是( ).A、 B、 C、 D、15. 如图,在同一直线上,甲、乙两人分别从A,B两点同时向右出发,甲、乙均为匀速,图2表示两人之间的距离y(m)与所经过的时间t(s)之间的函数关系图象,若乙的速度为1.5m/s,则经过30s,甲自A点移动了( ) A、45m B、7.2m C、52.2m D、57m16. 如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴的正半轴上,点B在第一象限,直线与边AB,BC分别交于点D,E,若点B的坐标为 , 则m的值可能是( )
A、45m B、7.2m C、52.2m D、57m16. 如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴的正半轴上,点B在第一象限,直线与边AB,BC分别交于点D,E,若点B的坐标为 , 则m的值可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 在平面直角坐标系中,点到原点O的距离 .18. 琪琪拿9元钱去买单价为1.5元/只的笔芯,买笔芯所剩的钱数y(元)与所买笔芯的数量x(只)之间的函数关系式为 .19. 如图,将一张矩形纸片沿着对角线向上折叠,使顶点C落到点E处,交于点F.过点D作 , 交于点G,连接交于点O.若 , , 则:
 (1)、四边形的形状是;(2)、的长为 .
(1)、四边形的形状是;(2)、的长为 .三、综合题
-
20. “你今天光盘了吗?”这是国家倡导厉行节约、反对浪费以来的时尚流行语.某校团委随机抽取了部分学生,对他们是否了解关于“光盘行动”的情况进行调查,调查结果有三种:A.了解很多;B.了解一点;C.不了解.团委根据调查的数据进行整理,绘制了如下尚不完整的扇形统计图和条形统计图.

请根据统计图中的信息,解答下列问题:
(1)、求本次活动共调查了多少名学生,并补全条形统计图;(2)、求出扇形统计图中B区域的圆心角度数.21. 如图,在平面直角坐标系中, , , .
( 1 )在图中作出关于x轴的对称图形;
( 2 )写出点 , , 的坐标,并求出的面积;
( 3 )若在x轴上存在点P使最小,则点P的坐标为 ▲ .
22. 如图,等边的边长是2,D,E分别为 , 的中点,连接 , , 过点E作交的延长线于点F. (1)、求证:四边形是平行四边形;(2)、求的长.23. 如图,在平面直角坐标系中,已知点O,A的坐标分别为 , .
(1)、求证:四边形是平行四边形;(2)、求的长.23. 如图,在平面直角坐标系中,已知点O,A的坐标分别为 , . (1)、点B的坐标是 , 点B与点A的位置关系是 . 现将点B、点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整点.在四边形内部(不包括边界)有整点M,使 , 请直接写出所有符合条件的点M的坐标.24. 如图1,两个全等的直角三角板ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,固定△ABC,将△DEF沿线段AB向右平移(即点D在线段AB上).回答下列问题:
(1)、点B的坐标是 , 点B与点A的位置关系是 . 现将点B、点A都向右平移5个单位长度分别得到对应点C和D,顺次连接点A,B,C,D,画出四边形;(2)、横、纵坐标都是整数的点称为整点.在四边形内部(不包括边界)有整点M,使 , 请直接写出所有符合条件的点M的坐标.24. 如图1,两个全等的直角三角板ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,固定△ABC,将△DEF沿线段AB向右平移(即点D在线段AB上).回答下列问题: (1)、如图2,连接CF,四边形ADFC的形状一定是形;(2)、如图3,当点D移动到AB的中点时,连接DC,CF,FB.求证:四边形CDBF是菱形.25. 如图1,为美化校园环境,某校计划在一块长为 , 宽为的长方形空地上修建一条宽为的甬道,余下的部分铺设草坪建成绿地.
(1)、如图2,连接CF,四边形ADFC的形状一定是形;(2)、如图3,当点D移动到AB的中点时,连接DC,CF,FB.求证:四边形CDBF是菱形.25. 如图1,为美化校园环境,某校计划在一块长为 , 宽为的长方形空地上修建一条宽为的甬道,余下的部分铺设草坪建成绿地. (1)、甬道的面积为 , 绿地的面积为;(用含a的代数式表示)(2)、已知某园林公司修建甬道、绿地的造价(元),(元)与修建面积之间的函数关系图像如图2所示.
(1)、甬道的面积为 , 绿地的面积为;(用含a的代数式表示)(2)、已知某园林公司修建甬道、绿地的造价(元),(元)与修建面积之间的函数关系图像如图2所示.①直接写出修建甬道的造价(元)、修建绿地的造价(元)与的关系式;
②如果学校决定由该公司承建此项目,并要求修建的甬道宽度不少于且不超过 , 那么甬道宽为多少时,修建的甬道和绿地的总造价最低?最低总造价为多少元?
26. 如图1,在平面直角坐标系中,四边形的顶点A,C分别在x轴、y轴的正半轴上,点A的坐标为 , , 直线经过点B,C. (1)、点C的坐标为( , ),点B的坐标为( , );(2)、设点P是x轴上的一个动点,若以点P,A,C为顶点的三角形是等腰三角形,求点P的坐标;(3)、如图2,直线l经过点C,与直线交于点M,作点O关于直线l的对称点 , 连接并延长 , 交直线于第一象限的点D.当时,求直线l的解析式.
(1)、点C的坐标为( , ),点B的坐标为( , );(2)、设点P是x轴上的一个动点,若以点P,A,C为顶点的三角形是等腰三角形,求点P的坐标;(3)、如图2,直线l经过点C,与直线交于点M,作点O关于直线l的对称点 , 连接并延长 , 交直线于第一象限的点D.当时,求直线l的解析式.