河北省保定市唐县2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、2. 函数y 中自变量x的取值范围是( )A、x>3 B、x≠3 C、x≥3 D、x≥03. 下列三条线段不能组成直角三角形的是( )A、a=5,b=12,c=13 B、a=6,b=8,c=10 C、 D、a:b:c=2:3:44. 在ABCD中,∠ABC的平分线交AD于E,∠BED=140°,则∠A的大小为( )
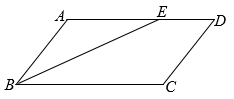 A、140° B、130° C、120° D、100°5. 计算的结果,估计在( )A、8与9之间 B、7与8之间 C、6与7之间 D、5与6之间6. 为了丰富校园文化,学校艺术节举行初中生书法大赛,设置了10个获奖名额.结果共有21名选手进入决赛,且决赛得分均不相同.若知道某位选手的决赛得分,要判断它是否获奖,只需知道学生决赛得分的( )A、平均数 B、中位数 C、众数 D、方差7. 已知点(-3,y1)、(4,y2)在函数 y=2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( )
A、140° B、130° C、120° D、100°5. 计算的结果,估计在( )A、8与9之间 B、7与8之间 C、6与7之间 D、5与6之间6. 为了丰富校园文化,学校艺术节举行初中生书法大赛,设置了10个获奖名额.结果共有21名选手进入决赛,且决赛得分均不相同.若知道某位选手的决赛得分,要判断它是否获奖,只需知道学生决赛得分的( )A、平均数 B、中位数 C、众数 D、方差7. 已知点(-3,y1)、(4,y2)在函数 y=2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定8. 在如图所示的计算程序中,y与x之间的函数关系所对应的图象应为( ) A、
A、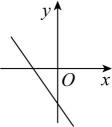 B、
B、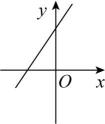 C、
C、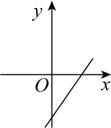 D、
D、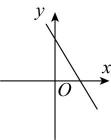 9. 实数a、b在数轴上的位置如图所示,化简:( )
9. 实数a、b在数轴上的位置如图所示,化简:( ) A、-b B、-2b+a C、a D、2b-a10. 如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升3cm到D点,则橡皮筋被拉长了( )
A、-b B、-2b+a C、a D、2b-a10. 如图,长为8cm的橡皮筋放置在数轴上,固定两端A和B,然后把中点C向上拉升3cm到D点,则橡皮筋被拉长了( )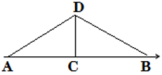 A、3cm B、2cm C、4cm D、2.5cm11. 如图,直线 与直线 交于点 ,则方程组 解是( )
A、3cm B、2cm C、4cm D、2.5cm11. 如图,直线 与直线 交于点 ,则方程组 解是( )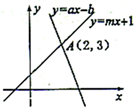 A、 B、 C、 D、12. 关于一次函数y= -3x+4图像和性质的描述不正确的是( )A、y 随x的增大而减小 B、直线与x轴交点的坐标是( 0, 4 ) C、当x>0时,y<4 D、直线经过第一、二、四象限13. 如图,四边形ABCD是矩形,连接AC.根据尺规作图痕迹,判断直线MN与CB的位置关系( )
A、 B、 C、 D、12. 关于一次函数y= -3x+4图像和性质的描述不正确的是( )A、y 随x的增大而减小 B、直线与x轴交点的坐标是( 0, 4 ) C、当x>0时,y<4 D、直线经过第一、二、四象限13. 如图,四边形ABCD是矩形,连接AC.根据尺规作图痕迹,判断直线MN与CB的位置关系( )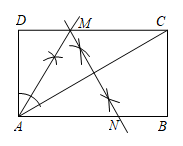 A、相交,夹角30° B、平行 C、相交,夹角60° D、垂直14. 某校在预防“新冠”期间,计划购买消毒液若干箱.已知,一次购买消毒液若不超过20箱,按定价80元付款;若超过20箱,超过部分按定价七折付款.设一次购买数量x(x>20)箱,付款金额为y元,则y与x的函数式为( )A、y=0.7×80x B、y=0.7x+80((x-10) C、y=0.7×80(x-20)+80×20 D、y=0.7×80((x-10)15. 如图所示,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )
A、相交,夹角30° B、平行 C、相交,夹角60° D、垂直14. 某校在预防“新冠”期间,计划购买消毒液若干箱.已知,一次购买消毒液若不超过20箱,按定价80元付款;若超过20箱,超过部分按定价七折付款.设一次购买数量x(x>20)箱,付款金额为y元,则y与x的函数式为( )A、y=0.7×80x B、y=0.7x+80((x-10) C、y=0.7×80(x-20)+80×20 D、y=0.7×80((x-10)15. 如图所示,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( )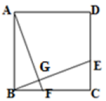 A、BE=AF B、∠DAF=∠BEC C、AG⊥BE D、∠AFB+∠BEC=90°16. 如图,△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1、l2、l3上,且l1、l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )
A、BE=AF B、∠DAF=∠BEC C、AG⊥BE D、∠AFB+∠BEC=90°16. 如图,△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1、l2、l3上,且l1、l2之间的距离为1,l2、l3之间的距离为3,则AC的长是( )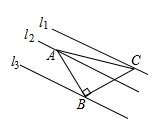 A、4 B、5 C、5 D、10
A、4 B、5 C、5 D、10二、填空题
-
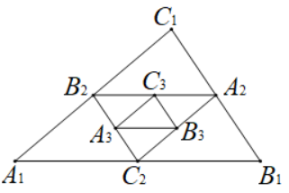
17. 化简: = .18. 将正比例函数的图像向上平移4个单位,则平移后所得函数解析式是 .19. 定义新运算“”:对于任意实数a和b,规定: . 例: . 则 .20. 如图A1B1C1中,A1B1=8,B1C1=4,A1C1=6,依次连接A1B1C1的三边中点,得到A2B2C2;再依次连接A2B2C2三边中点,得到A3B3C3;….则的周长是 .
三、解答题
-
21. 计算题(1)、(2)、22. 作图题(1)、填空:如果长方形的长为3,宽为2,那么对角线的长为 .(2)、如下图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点(端点),分别按下列要求画图(不要求写画法和证明,但要标注顶点).
 ①在图1中,分别画三条线段AB、CD、EF,使AB=、CD=、EF= .
①在图1中,分别画三条线段AB、CD、EF,使AB=、CD=、EF= . ②在图2中,画三角形ABC,使AB=3、BC=、CA= .
③在图3中,画平行四边形ABCD,使 , 且面积为6.
23. 某校举行了“珍爱生命,预防溺水”主题知识竞赛活动,八(1)、八(2)班各选取五名选手参赛.两班参赛选手成绩依次如下:(单位:分)甲:8,8,7,8,9
乙:5,9,7,10,9
学校根据两班的成绩绘制了如下不完整的统计图表:
班级
平均数
众数
中位数
方差
八(1)
8
b
8
0.4
八(2)
a
9
c
3.2
根据以上信息,请解答下面的问题:
(1)、a= , b= , c=;(2)、学校根据这些学生的成绩,确定八(1)班为获胜班级,请问学校评定的依据是什么?(3)、若八(2)班又有一名学生参赛,考试成绩是8分,则八(2)班这6名选手成绩的平均数与5名选手成绩的平均数相比会 . (选填“变大”“变小”或“不变”)24. 如图,∠A=∠B=40°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.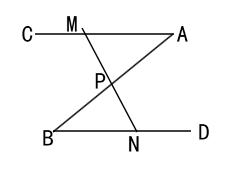 (1)、求证:APMBPN;(2)、当α等于多少度时,以A、M、B、N为顶点的四边形是菱形?25. 面临毕业季,某电脑营销商瞄准时机,在五月底筹集到资金12.12万元,用于一次性购进A、B两种型号的电脑共30台.根据市场需求,这些电脑可以全部销售,全部销售后利润不少于1.6万元,其中电脑的进价和售价见下表:
(1)、求证:APMBPN;(2)、当α等于多少度时,以A、M、B、N为顶点的四边形是菱形?25. 面临毕业季,某电脑营销商瞄准时机,在五月底筹集到资金12.12万元,用于一次性购进A、B两种型号的电脑共30台.根据市场需求,这些电脑可以全部销售,全部销售后利润不少于1.6万元,其中电脑的进价和售价见下表:A型电脑
B型电脑
进价(元/台)
4200
3600
售价(元/台)
4800
4000
设营销商计划购进A型电脑x台,电脑全部销售后获得的利润为y元.
(1)、试写出y与x的函数关系式;(2)、该营销商有几种购进电脑的方案可供选择?(3)、该营销商选择哪种购进电脑的方案获利最大?最大利润是多少?26. 如图,在平面直角坐标系中,矩形ABCD顶点A、B、C的坐标分别为(0,6)、(0,2)、(4,2),直线l:y=kx+5-3k(k>0).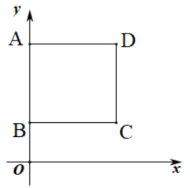 (1)、点D的坐标是;(2)、若直线l:y=kx+5-3k经过点D,求直线l的解析式;(3)、在(2)的条件下,若直线l与BC、x轴分别交于点E、F,求CEF的面积;(4)、在(2)的条件下,若点P(x,y)是第一象限内直线l上的一个动点,当点P运动过程中,是否存在CEP为等腰三角形?若存在直接写出满足条件的点P的个数.
(1)、点D的坐标是;(2)、若直线l:y=kx+5-3k经过点D,求直线l的解析式;(3)、在(2)的条件下,若直线l与BC、x轴分别交于点E、F,求CEF的面积;(4)、在(2)的条件下,若点P(x,y)是第一象限内直线l上的一个动点,当点P运动过程中,是否存在CEP为等腰三角形?若存在直接写出满足条件的点P的个数.