河北省保定市安新县2020-2021学年八年级下学期期末考试数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{4}$ 的结果是（）

A、 $\pm 2$ B、2 C、 $- 2$ D、4

查看试题解析
2. 直线 $y = k x - 4$ 经过点（−2，2），则该直线的解析式是（）

A、 $y = - 3 x - 4$ B、 $y = - x - 4$ C、 $y = x - 4$ D、 $y = 3 x - 4$

查看试题解析
3. 如图，在△ABC中，∠ABC＝90°，分别以BC，AB，AC为边向外作正方形面积分别记为S₁ ， S₂ ， S₃ ．若S₂＝6，S₃＝10．则面积为S₁的正方形的边长为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 某校在体育健康测试中，有8名男生“引体向上”的成绩（单位：次）分别是：14，12，8，9，16，12，7，10，这组数据的中位数和众数分别是（）

A、10，12 B、12，11 C、11，12 D、12，12

查看试题解析
5. 如果点A（1，m）与点B（3，n）都在直线y＝﹣2x+1上，那么m与n的关系是（）

A、m＞n B、m＜n C、m＝n D、不能确定

查看试题解析
6. 如图，平行四边形ABCD的对角线AC和BD相交于点O，且两条对角线的和为36cm，AB的长为9cm，则△OCD的周长为（）

A、45cm B、27cm C、22.5cm D、31cm

查看试题解析
7. 矩形、菱形、正方形都具有的性质是（）．

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

查看试题解析

8. 下表记录了甲、乙、丙、丁四名同学最近几次数学考试成绩的平均数与方差：

	甲	乙	丙	丁
平均数（分）	92	95	95	92
方差	3.6	3.6	7.4	8.1

要选择一名成绩好且发挥稳定的同学参加数学比赛，应该选择( )

A、甲 B、乙 C、丙 D、丁

查看试题解析

9. 如图，点О是矩形ABCD的对角线AC的中点，点M是AD的中点．若 $A B = 5$ ， $B C = 12$ ，则四边形ABOM的周长是（）

A、24 B、21 C、23 D、20

查看试题解析
10. 将直线y＝2x+2向上平移4个单位长度后，直线与坐标轴围成的三角形的面积增加了（）

A、9 B、2 C、14 D、8

查看试题解析
11. 如图，在矩形ABCD中，点E在AD上， $E F ⊥ E C$ ， $E F = E C$ ， $D E = 2$ ，矩形周长为16，则AE的长是（）

A、2 B、3 C、4 D、5

查看试题解析
12. 某区中考体育加试女子800米耐力测试中，同时起跑的甲和乙所跑的路程S（米）与所用时间t（秒）之间的函数图象分别为线段OA和折线OBCD，下列说法正确的是（）

A、甲的速度随时间的增大而增大 B、乙的平均速度比甲的平均速度大 C、在起跑后50秒时，甲在乙的前面 D、在起跑后180秒时，两人之间的距离最远

查看试题解析
13. 如图，在四边形ABCD中，AD＝BC，E，F，G分别是AB，CD，AC的中点，若∠DAC＝20°，∠ACB＝84°，则∠FEG等于（）

A、32° B、38° C、64° D、30°

查看试题解析
14. 如图，直线y＝kx＋b经过点A(－1，－2)和点B(－2，0)，直线y＝2x过点A，则不等式2x＜kx＋b＜0的解集为（）

A、x＜－2 B、－2＜x＜－1 C、－2＜x＜0 D、－1＜x＜0

查看试题解析
15. 如图，在平面直角坐标系xOy中，菱形 $A B C D$ 的顶点 $D$ 在 $x$ 轴上，边 $B C$ 在 $y$ 轴上，若点 $A$ 的坐标为(12，13)，则点 $C$ 的坐标是（）

A、(0，-5) B、(0，-6) C、(0，-7) D、(0，-8)

查看试题解析
16. 如图，点E为平行四边形ABCD边上的一个动点，并沿A→B→C→D的路径移动到点D停止，设点E经过的路径长为x，△ADE的面积为y，则下列图象能大致反映y与x的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

17. 在平面直角坐标系xOy中，点A（2，﹣3）关于x轴对称的点B的坐标是.

查看试题解析
18. 在平面直角坐标系xOy中，一次函数 $y = kx$ 和 $y = - x + 3$ 的图象如图所示，则二元一次方程组 ${\begin{cases} y = kx \\ y = - x + 3 \end{cases}$ 的解为．

查看试题解析
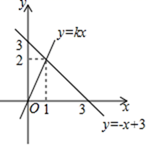19. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝45°，AB＝4cm，点P从点A出发，以2cm/s的速度沿边AB向终点B运动（到点B时停止）．过点P作PQ⊥AB交折线ACB于点Q，D为PQ中点，以DQ为边向右侧作正方形DEFQ．设点P的运动时间为x（s）．

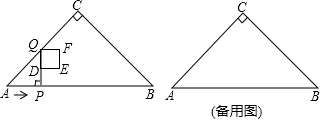(1)、当点Q在边AC上时，正方形DEFQ的边长为 cm（用含x的代数式表示）；

(2)、当点F落在边BC上时，x的值为；

(3)、当边BC的中点落在正方形DEFQ内部时，x的取值范围为．

查看试题解析

三、解答题

20. 计算：（ $\sqrt{5}$ ﹣1）（ $\sqrt{5}$ +1）+|1﹣ $\sqrt{2}$ |．

查看试题解析
21. 如图，AE//BF，AC平分∠BAE，交BF于点C，BD平分∠ABF交AE于点D，连接CD，求证：四边形ABCD是菱形．

查看试题解析

22. 某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如条形图所示．

下面是根据5名选手的决赛成绩的条形图绘制的关于平均数、中位数、众数方差的统计表．

	平均数/分	中位数/分	众数/分	方差/分²
初中代表队	a	85	b	$S_{初中}^{2}$
高中代表队	85	c	100	160

(1)、根据条形图计算出a，b，c的值：a＝， b＝， c＝．

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算初中代表队决赛成绩的方差

S_{初 中}^{2}

，并判断哪一个代表队选手的成绩较为稳定．

查看试题解析

23. 如图，在平面直角坐标系中，A，B，C三点的坐标分别为（2，0），（1，2），（4，3），直线l的解析式为y＝kx+4﹣3k（k≠0）．

(1)、当k＝1时，直线l与x轴交于点D，点D的坐标是， S_△ABD＝．

(2)、小明认为点C在直线l上，他的判断是否正确，请说明理由；

(3)、若线段AB与直线l有交点，则k的取值范围为．

查看试题解析
24. 有甲、乙两种客车，2辆甲种客车与3辆乙种客车的总载客量为180人，1辆甲种客车与2辆乙种客车的总载客量为105人．

(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人？

(2)、某学校组织240名师生集体外出活动，拟租用甲、乙两种客车共6辆，一次将全部师生送到指定地点．若每辆甲种客车的租金为400元，每辆乙种客车的租金为280元，请给出最节省费用的租车方案，并求出最低费用．

查看试题解析
25. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

(1)、求证：△AEF≌△DEB；

(2)、若∠BAC＝90°，试判断四边形ADCF的形状，并证明你的结论．

查看试题解析
26. 如图，在平面直角坐标系中，直线 $l_{1}$ 交x轴于点A，交y轴于点B，点B的坐标为 $(0 ， 3)$ ．直线 $l_{2}$ ： $y = 2 x$ 与直线 $l_{1}$ 相交于点C，点C的横坐标为1．

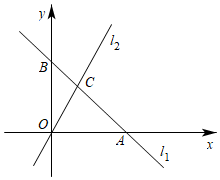(1)、求直线 $l_{1}$ 的解析式；

(2)、若点D是y轴上一点，且 $△ O C D$ 的面积是 $△ A O C$ 面积的 $\frac{2}{3}$ ，求点D的坐标；

(3)、平面内是否存在一点E，使得以点O，A，C，E为顶点的四边形是平行四边形?若存在，直接写出符合条件的点E的坐标；若不存在，说明理由．

查看试题解析