北京市平谷区2020-2021学年八年级下学期期末数学试题
试卷更新日期:2022-04-11 类型:期末考试
一、单选题
-
1. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在平面直角坐标系中,点M(2,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 矩形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四边相等4. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、5. 一次函数y=﹣2x+3的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 足球的照片(如图),则照片中心的一块黑色皮块的内角和是( )
2. 在平面直角坐标系中,点M(2,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 矩形具有而平行四边形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四边相等4. 用配方法解一元二次方程 , 配方后得到的方程是( )A、 B、 C、 D、5. 一次函数y=﹣2x+3的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 足球的照片(如图),则照片中心的一块黑色皮块的内角和是( ) A、180° B、360° C、540° D、720°7. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 设金色纸边的宽为xcm,那么x满足的方程是( )
A、180° B、360° C、540° D、720°7. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2 , 设金色纸边的宽为xcm,那么x满足的方程是( ) A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=08. 如图,四边形 ABCD 是菱形,其中 A,B 两点的坐标为A(0,3),B(4,0),则点 D 的坐标为( )
A、x2+130x﹣1400=0 B、x2+65x﹣350=0 C、x2﹣130x﹣1400=0 D、x2﹣65x﹣350=08. 如图,四边形 ABCD 是菱形,其中 A,B 两点的坐标为A(0,3),B(4,0),则点 D 的坐标为( ) A、(0,1) B、(0,-1) C、(0,2) D、(0,-2)
A、(0,1) B、(0,-1) C、(0,2) D、(0,-2)二、填空题
-
9. 反比例函数的图象经过点P(﹣1,2),则此反比例函数的解析式为 .10. 已知点 A(x,-2)与 B(6,y)关于原点对称,则 x+y= .11. 如图,中两个邻角的度数比为1:3,则其中较小的内角的度数为 .
 12. 函数和的图象交于点 P (3,-2 ),则根据图象可得,关于 的二元一次方程组的解是 .13. 如图,矩形ABCD中,E,F分别是AB, AD的中点,若EF=3,则AC的长是 .
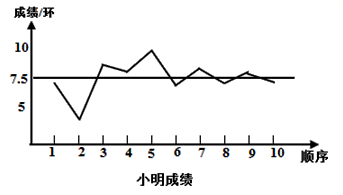
12. 函数和的图象交于点 P (3,-2 ),则根据图象可得,关于 的二元一次方程组的解是 .13. 如图,矩形ABCD中,E,F分别是AB, AD的中点,若EF=3,则AC的长是 .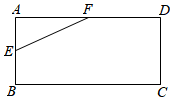 14. 要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择(填“小华”或“小明”)参加射击比赛;理由是 .
14. 要从小华、小明两名射击运动员中选择一名运动员参加射击比赛,在赛前对他们进行了一次选拔赛,下图为小华、小明两人在选拔赛中各射击10次成绩的折线图和表示平均数的水平线.你认为应该选择(填“小华”或“小明”)参加射击比赛;理由是 .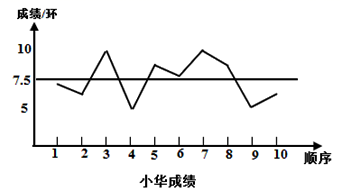
 15. 若一元二次方程 有一个根为 ,则k= .16. 图1中菱形的两条对角线长分别为6和8,将其沿对角线裁分为四个三角形,将这四个三角形无重叠地拼成如图2所示的图形,则图1中菱形的面积等于;图2中间的小四边形的面积等于 .
15. 若一元二次方程 有一个根为 ,则k= .16. 图1中菱形的两条对角线长分别为6和8,将其沿对角线裁分为四个三角形,将这四个三角形无重叠地拼成如图2所示的图形,则图1中菱形的面积等于;图2中间的小四边形的面积等于 .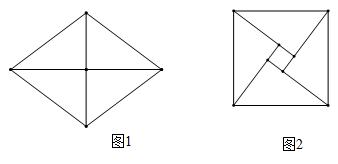
三、解答题
-
17. 解方程:(1)、;(2)、 .18. 在平面直角坐标系xOy中,已知直线AB与x轴交于A点 (2,0)与y轴交于点B(0,1).(1)、求直线AB的解析式;(2)、点M(-1,y1),N(3,y2)在直线AB上,比较y1与y2的大小.(3)、若x轴上有一点C,且S△ABC=2,求点C的坐标19. 如图,在直角△中,点D,E,F分别是边 , , 的中点.
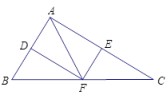 (1)、求证:四边形为矩形;(2)、若 , , 求出矩形的周长.20. 关于x的一元二次方程有两个不相等的实数根.(1)、求k的取值范围;(2)、请选择一个符合条件的整数k,并求方程的根.21.
(1)、求证:四边形为矩形;(2)、若 , , 求出矩形的周长.20. 关于x的一元二次方程有两个不相等的实数根.(1)、求k的取值范围;(2)、请选择一个符合条件的整数k,并求方程的根.21.“五一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游。
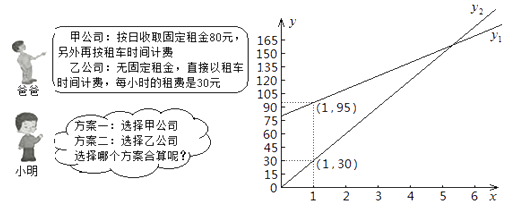
根据以上信息,解答下列问题:
(1)、设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;(2)、请你帮助小明计算并选择哪个出游方案合算。22. 下面是小红设计的“在矩形内作正方形”的尺规作图过程.已知:四边形ABCD为矩形.
求作:正方形ABEF(E在BC上,点F在AD上).
作法:①以A为圆心,AB为半径作弧, 交 AD于点F;
②以B为圆心,AB为半径作弧, 交 BC于点E;
③连接EF.
所以四边形ABEF为所求的正方形.
(1)、根据小红设计的尺规作图过程,使用直尺和圆规,补全图形(保留作图痕迹); (2)、完成下面证明.
(2)、完成下面证明.证明:∵AF=AB,BE=AB
∴ ▲ = ▲
在矩形ABCD中,AD∥BC,
即AF∥BE
∴四边形ABEF为平行四边形
∵∠A=90°
∴为矩形( )
∵AF=AB,
∴四边形ABEF为正方形 ( )
23. 垃圾分类是指按一定规定或标准将垃圾分类储存、投放和搬运,从而转变成公共资源的一系列活动的总称.做好垃圾分类有减少环境污染,节省土地资源等好处.平谷区广大党员积极参与社区桶前职守活动.其中,A社区有500名党员,为了解本社区3月—4月期间党员参加桶前职守的情况,A社区针对桶前职守的时长随机抽取50名党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息:a.桶前职守时长的频数分布表
时长x/小时
频数
频率
0 ≤ x < 10
8
0.16
10 ≤ x < 20
10
0.20
20 ≤ x < 30
16
b
30 ≤ x <40
12
0.24
40 ≤ x <50
a
0.08
b.桶前职守时长的频数分布直方图

c.其中,时长在20≤ x < 30这一组的数据是:20 20 21 21 22 24 24 26 26 27 27 28 28 28 29 29.请根据所给信息,解答下列问题:
(1)、a= , b=;(2)、请补全频数分布直方图;(3)、其中这50名党员桶前职守时长的中位数是;(4)、估计3月—4月期间A社区党员参加桶前职守的时长不低于30小时的有人.24. 如图,在正方形ABCD中,点P在直线BC上,作射线AP,将射线AP绕点A逆时针旋转45°,得到射线AQ,交直线CD于点Q,过点B作BE⊥AP于点E,交AQ于点F,连接DF. (1)、依题意补全图形;(2)、用等式表示线段BE,EF,DF之间的数量关系,并证明.25. 对于平面直角坐标系xOy中的图形M和点P,给出如下定义:将图形M绕点P顺时针旋转90°得到图形N,图形N称为图形M关于点P的“垂直图形”.例如,图1中点D为点C关于点P的“垂直图形”.
(1)、依题意补全图形;(2)、用等式表示线段BE,EF,DF之间的数量关系,并证明.25. 对于平面直角坐标系xOy中的图形M和点P,给出如下定义:将图形M绕点P顺时针旋转90°得到图形N,图形N称为图形M关于点P的“垂直图形”.例如,图1中点D为点C关于点P的“垂直图形”.
 (1)、点A关于原点O的“垂直图形”为点B.
(1)、点A关于原点O的“垂直图形”为点B.①若点A的坐标为(0,2),则点B的坐标为;
②若点B的坐标为(2,1),则点A的坐标为 .
(2)、E(-3,3),F(a,0).点E关于点F的“垂直图形”记为 , 求点的坐标(用含a的式子表示).