北京市东城区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 函数 $y = \frac{1}{x + 1}$ 的自变量的取值范围是（）

A、 $x \geq - 1$ B、 $x \leq - 1$ C、 $x \neq - 1$ D、 $x \neq 1$

查看试题解析
2. 如图，数轴上点B表示的数为1， $A B ⊥ O B$ ，且 $A B = O B$ ，以原点O为圆心， $O A$ 为半径画弧，交数轴正半轴于点C，则点C所表示的数为（　　　）

A、 $\sqrt{2}$ B、 $- \sqrt{2}$ C、 $\sqrt{2} - 1$ D、 $1 - \sqrt{2}$

查看试题解析
3. 为筹备学校元旦联欢晚会，在准备工作中，班长先对全班同学喜爱的水果做了民意调查，再决定最终买哪种水果．下面的统计量中，他最关注的是（　　　）

A、众数 B、平均数 C、中位数 D、方差

查看试题解析
4. 下列各组数中，能作为直角三角形边长的是（　　　）

A、1，2，3 B、6，7，8 C、1，1， $\sqrt{3}$ D、5，12，13

查看试题解析
5. 一次函数 $y = 3 x + 1$ 的图象经过点 $(1 ， y_{1})$ ， $(2 ， y_{2})$ ，则以下判断正确的是（　　　）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
6. 在平面直角坐标系 $x O y$ 中，将直线 $y = 2 x + 1$ 向上平移2个单位长度后，所得的直线的解析式为（　　　）

A、 $y = 2 x - 1$ B、 $y = 2 x + 2$ C、 $y = 2 x + 3$ D、 $y = 2 x - 2$

查看试题解析
7. 菱形和矩形都具有的性质是（　　　）

A、对角线互相垂直 B、对角线长度相等 C、对角线平分一组对角 D、对角线互相平分

查看试题解析
8. 甲、乙、丙、丁四位同学五次数学测验成绩统计如表．如果从这四位同学中，选出一位平均成绩较高且状态稳定的同学参加数学比赛，那么应选（　　　）

甲
乙
丙
丁
平均数
80
85
85
80
方差
42
45
54
59

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 如图，在 $△ A B C$ 中，点D、点E分别是 $A B$ ， $A C$ 的中点，点F是 $D E$ 上一点，且 $∠ A F C = 90 °$ ，若 $B C = 12$ ， $A C = 8$ ，则 $D F$ 的长为（　　　）

A、1 B、2 C、3 D、4

查看试题解析
10. 若定义一种新运算： $a \otimes b = {\begin{array}{l} 2 a - b (a \geq b) \\ 2 a + b - 12 (a < b) \end{array}$ ，例如： $3 \otimes 1 = 2 \times 3 - 1 = 5$ ； $4 \otimes 5 = 2 \times 4 + 5 - 12 = 1$ ．则函数 $y = (x + 2) \otimes (2 x - 2)$ 的图象大致是（　　　）

A、 B、 C、 D、

查看试题解析

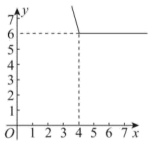
二、填空题

11. 请写出一个图形经过一、三象限的正比例函数的解析式．

查看试题解析
12. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 100 °$ ，则 $∠ A =$ ．

查看试题解析
13. 某手表厂抽查了10只手表的日走时误差，数据如下表所示：

日走时误差

（单位：秒）

0

1

2

3

只数

4

3

2

1

则这10只手表的平均日走时误差是秒．

查看试题解析
14. 如图，在平面直角坐标系 $x O y$ 中，函数 $y_{1} = k x$ 与 $y_{2} = a x + 3$ 的图象交于点 $A (- 1 ， 2)$ ，则关于x的不等式 $k x > a x + 3$ 的解集是．

查看试题解析
15. 如图，已知P是正方形ABCD对角线BD上一点，且BP＝BC ，则∠ACP度数是度．

查看试题解析
16. 我国三国时期数学家赵爽为了证明勾股定理，创造了一副“弦图”，后人称其为“赵爽弦图”，如图1所示．在图2中，若正方形 $A B C D$ 的边长为14，正方形 $I J K L$ 的边长为2，且 $I J ∥ A B$ ，则正方形 $E F G H$ 的边长为．

查看试题解析
17. 如图，把矩形 $A B C D$ 沿直线 $B D$ 向上折叠，使点C落在点 $C^{'}$ 的位置上， $B C^{'}$ 交 $A D$ 于点E，若 $A B = 3$ ， $B C = 6$ ，则 $D E$ 的长为．

查看试题解析
18. 如图，菱形 $A B C D$ 的边长为4， $∠ A B C = 60 °$ ，点 $E$ 是 $C D$ 的中点，点 $M$ 是 $A C$ 上一动点，则 $M D + M E$ 的最小值是．

查看试题解析

三、解答题

19. 已知：如图1， $△ A B C$ 为锐角三角形， $A B = A C$ ．
求作：菱形 $A B D C$ ．
作法：如图2．
①以点A为圆心，适当长为半径作弧，交 $A C$ 于点M，交 $A B$ 于点N；
②分别以点M，N为圆心，大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧在 $∠ C A B$ 的内部相交于点E，作射线 $A E$ 与 $B C$ 交于点O；
③以点O为圆心，以 $O A$ 长为半径作弧，与射线 $A E$ 交于点D，点D和点A分别位于 $B C$ 的两侧，连接 $C D$ ， $B D$ ；则四边形 $A B D C$ 就是所求作的菱形．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：由作法可知， $A E$ 平分 $∠ C A B$ ．
$∵ A B = A C$ ，
$∴ C O =$             ▲             ．
$∵ A O = D O$ ，
$∴$ 四边形 $A B D C$ 是平行四边形（       ）（填推理的依据）．
$∵ A B = A C$ ，
$∴$ 四边形 $A B D C$ 是菱形（        ）（填推理的依据）．

查看试题解析
20. 如图，在 $▱ A B C D$ 中，点 $E$ ， $F$ 分别在 $A D$ 、 $B C$ 上，且 $A E = C F$ ，连接 $E F$ ， $A C$ 交于点 $O$ ．求证： $O E = O F$ ．

查看试题解析
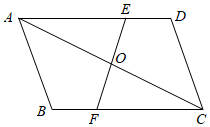21. 下表是一次函数 $y = k x + b$ （k，b为常数， $k \neq 0$ ）中y与x的两组对应值．
$x$
-2
0
$y$
6
3

(1)、求这个一次函数的表达式；

(2)、求这个一次函数图象与坐标轴围成的三角形的面积．

查看试题解析
22. 如图，在 $4 \times 4$ 的正方形网格中，每个小方格的顶点叫做格点，以格点为顶点分别按下列要求画三角形 $A B C$ ．

(1)、在图①中，画一个直角三角形，使它的三边长都是有理数；

(2)、在图②中，画一个直角三角形，使它的两边长是有理数，另外一边长是无理数；

(3)、在图③中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数．

查看试题解析
23. 2021年7月1日是中国共产党成立100周年纪念日．某校开展了一次党史知识竞赛（竞赛成绩为百分制），并随机抽取了50名学生的竞赛成绩，经过整理数据，得到以下信息：
信息一：50名学生竞赛成绩的频数分布直方图如图所示（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ），从左到右依次为第一组到第五组．
信息二：第三组的成绩（单位：分）为71，72，73，73，74，74，75，76，76，76，77，79．
根据信息解答下列问题：

(1)、补全频数分布直方图（直接在图中补全）；

(2)、第三组竞赛成绩的众数是分，抽取的50名学生竞赛成绩的中位数是分；

(3)、若该校共有1500名学生参赛，估计该校参赛学生成绩不低于80分的人数．

查看试题解析
24. 如图，在平面直角坐标系 $x O y$ 中，直线 $l_{1}$ 经过原点，且与直线 $l_{2} ： y = - x + 3$ 交于点 $A (m ， 2)$ ，直线 $l_{2}$ 与 $x$ 轴交于点 $B$ ．

(1)、求直线 $l_{1}$ 的函数解析式；

(2)、点 $P (n ， 0)$ 在 $x$ 轴上，过点 $P$ 作平行于 $y$ 轴的直线，分别与直线 $l_{1}$ ， $l_{2}$ 交于点 $M$ ， $N$ .若 $M N = O B$ ，求 $n$ 的值．

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $A B = C D = 6$ ， $B C = 10$ ， $A C = 8$ ， $∠ A B C = ∠ B C D$ .过点 $D$ 作 $D E ⊥ B C$ ，垂足为点 $E$ ，延长 $D E$ 至点 $F$ ，使 $E F = D E$ ，连接 $B F$ ， $C F$ ．

(1)、求证：四边形 $A B F C$ 是矩形；

(2)、求 $D E$ 的长．

查看试题解析
26. 某种机器工作前先将空油箱加满（加油过程），然后停止加油立即开始工作（加工过程）．当停止工作时，油箱中油量为10升．在整个过程中，油箱里的油量y（单位：升）与时间x（单位：分）之间的关系如图所示．

(1)、机器加油过程中每分钟加油量为升，机器加工过程中每分钟耗油量为升；

(2)、求机器加工过程中y关于x的函数解析式；

(3)、当油箱中油量为油箱容积的一半时，直接写出此时x的值．

查看试题解析
27. 如图，点P是正方形 $A B C D$ 边 $B C$ 上一点， $∠ B A P = α$ .作点D关于直线 $A P$ 的对称点E，连接 $A E$ .作射线 $E B$ 交直线 $A P$ 于点F，连接 $C F$ ．

(1)、依题意补全图形；

(2)、求 $∠ A B E$ 的度数（用含 $α$ 的式子表示）；

(3)、① $∠ A F B =$ °；
②用等式表示 $B E$ ， $C F$ 的数量关系，并给出证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中的图形M和点P，给出如下定义：如果图形M上存在点Q，使得 $0 \leq P Q \leq 1$ ，那么称点P为图形M的和谐点．已知点 $A (3 ， 3)$ ， $B (- 3 ， 3)$ ．

(1)、在点 $P_{1} (- 2 ， 2)$ ， $P_{2} (0 ， 3.5)$ ， $P_{3} (4 ， 0)$ 中，直线 $A B$ 的和谐点是；

(2)、点P在直线 $y = x - 1$ 上，如果点P是直线 $A B$ 的和谐点，求点P的横坐标x的取值范围；

(3)、已知点 $C (- 3 ， - 3)$ ， $D (3 ， - 3)$ ，如果直线 $y = x + b$ 上存在正方形 $A B C D$ 的和谐点E，F，使得线段 $E F$ 上的所有点（含端点）都是正方形 $A B C D$ 的和谐点，且 $E F > \sqrt{2}$ ，直接写出b的取值范围．

查看试题解析

	甲	乙	丙	丁
平均数	80	85	85	80
方差	42	45	54	59

$x$	-2	0
$y$	6	3