北京市昌平区2020-2021学年八年级下学期期末数学试题

试卷更新日期：2022-04-11 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标中，点 $M (- 2 ， 3)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 云纹，指云形纹饰，是古代中国吉祥图案，象征高升和如意，被广泛地运用于装饰中．下列云纹图案中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图，足球图片正中的黑色正五边形的内角和是（）.

A、180° B、360° C、540° D、720°

查看试题解析
4. 已知直线y＝kx+2与直线y＝2x平行，则k的值是（　　）

A、2 B、﹣2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析

5. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	185	180	185	180
方差	3.6	3.6	7.4	8.1

根据表数据，从中选择一名成绩好且发挥稳定的参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 第七次全国人口普查结果发布：全国人口数超14.1亿，人口老龄化严重，2018年60岁及以上人口24949万人，2020年60岁及以上人口达到26402万人，设2018年到2020年60岁及以上人口的年平均增长率为x，则根据题意列出方程（　　）

A、24949（1+x）²＝26402 B、26402（1+x）²＝24949 C、24949（1﹣x）²＝26402 D、26402（1﹣x）²＝24949

查看试题解析
7. 如图，在四边形ABCD中，AB $/ /$ CD．下列条件不能判定此四边形为平行四边形的是（　　）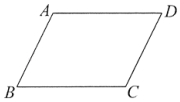

A、AB＝CD B、AD $/ /$ BC C、∠B＝∠D D、AD＝BC

查看试题解析
8. 根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（　　）
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09

A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25＜x＜3.26

查看试题解析

二、填空题

9. 请写出一个过点（0，1）的函数的表达式．

查看试题解析
10. 如图，在 $Rt Δ A B C$ 中， $∠ A C B = 90^{°}$ ，D是AB的中点，若 $∠ A = 26^{°}$ ，则 $∠ B D C$ 的度数为。

查看试题解析
11. 如图，A、B两点分别位于一个池塘的两端，小聪想用绳子测量A、B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A、B的点C ，找到AC、BC的中点D、E ，并且测出DE的长为10m，则A、B间的距离为．

查看试题解析
12. 直线y＝﹣2x+a经过（3，y₁）和（﹣2，y₂），则y₁y₂ ．（填写“＞”，“＜”或“＝”）

查看试题解析
13. 如图，在矩形ABCD中，对角线AC，BD交于点O，若∠AOD＝120°，BD＝6，则AB的长为．

查看试题解析
14. 如图，已知函数y=x+b和y=ax+3的图象交点为P，则不等式x+b＞ax+3的解集为．

查看试题解析
15. 如图，菱形ABCD的两条对角线AC，BD交于点O，BE⊥AD于点E，若AC＝8，BD＝6，则BE的长为．

查看试题解析
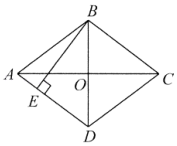16. 若一个函数图象经过点A（1，3），B（3，1），则关于此函数的说法：
①该函数可能是一次函数；
②点P（2，2.5），Q（2，3.5）不可能同时在该函数图象上；
③函数值y一定随自变量x的增大而减小；
④可能存在自变量x的某个取值范围，在这个范围内函数值y随自变量x增大而增大．
所有正确结论的序号是．

查看试题解析
17. A、B两地相距80km，甲、乙两人沿同一条路从A地到B地，l₁ ， l₂分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．

(1)、乙出发h后，甲才出发；

(2)、在乙出发h后，两人相遇，这时他们离开A地m；

(3)、甲的速度是km/h，乙的速度是km/h．

查看试题解析

三、解答题

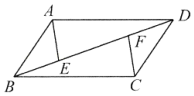
18. 解方程：x²﹣4x﹣5＝0.

查看试题解析
19. 如图，在▱ABCD中，E，F是对角线BD上的两点，且BE＝DF，连接AE，CF．求证：AE＝CF．

查看试题解析
20. 一次函数y＝kx+b（k≠0）的图象经过点A（1，6）和点B（0，4）．

(1)、求一次函数的表达式；

(2)、若此一次函数图象与x轴交于点C，求△BOC的面积．

查看试题解析
21. 关于x的一元二次方程x²﹣4x+3m＝0有实数根．

(1)、求m的取值范围；

(2)、写出一个符合条件的m的值，求出此时方程的根．

查看试题解析
22. 在平面直角坐标系中，四边形ABCD为矩形，A（﹣1，m）和B（n，2）关于y轴对称．

(1)、m＝， n＝；

(2)、矩形ABCD的中心在原点O，直线y＝x+b与矩形ABCD交于P，Q两点．
①当b＝0时，线段PQ长度为　 ▲ 　；
②当线段PQ长度最大时，求b的取值范围．

查看试题解析
23. 下面是小静设计的作矩形ABCD的尺规作图过程．
已知：Rt△ABC中，∠ABC＝90°．

求作：矩形ABCD．

作法：如图，

①以点A为圆心，AB长为半径作弧，交BA的延长线于点E；

②分别以点B，E为圆心，大于 $\frac{1}{2}$ BE长为半径作弧，两弧交于点F，作直线AF；

③以点C为圆心，BC长为半径作弧，交BC的延长线于点M；

④分别以点B，M为圆心，大于 $\frac{1}{2}$ BM长为半径作弧，两弧交于点N，作直线CN；

⑤直线AF与直线CN交于点D；

所以四边形ABCD是矩形．

(1)、根据小静设计的尺规作图过程，使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：
∵AB＝　▲　， BF＝　▲　，
∴AF⊥BE．（）（填推理的依据）
同理CN⊥BM．
又∵∠ABC＝90°，
∴四边形ABCD是矩形．（）（填推理的依据）

查看试题解析
24. 已知：如图，在等腰△ABC中，AB＝BC，BO平分∠ABC交AC于点O，延长BO至点D，使OD＝BO，连接AD，CD，过点D作DE⊥BD交BC的延长线于点E．

(1)、求证：四边形ABCD是菱形；

(2)、如果AB＝2，∠BAD＝60°，求DE的长．

查看试题解析

25. 2021年是中国共产党建党100周年，为了让学生了解更多的党史知识，某中学初二年级举行了一次“党史知识竞赛”，为了了解本次竞赛情况，从中抽取了初二年级50名学生，对他们此次竞赛的成绩（得分取正整数，满分为100分）整理并绘制了如下统计图表．

初二年级学生竞赛成绩的频数分布表

成绩分组/分	频数	频率
40≤x＜50	1	0.02
50≤x＜60	a	0.06
60≤x＜70	10	0.20
70≤x＜80	b	c
80≤x＜90	12	0.24
90≤x＜100	18	0.36
合计	50	1.00

根据以上信息，回答下列问题：

(1)、a＝， b＝， c＝；

(2)、补全频数分布直方图；

(3)、已知该校初二年级有学生400人，估计该校初二年级学生竞赛成绩不低于80分的人数．

查看试题解析

26. 如图，在平面直角坐标系xOy中，直线y＝kx+2与直线y＝x﹣2交于点A（3，m）．

(1)、求k、m的值；

(2)、已知点P（n，n），过点P作垂直于y轴的直线，交直线y＝x﹣2于点M，过点P作垂直于x轴的直线，交直线y＝kx+2于点N．
①当n＝3时，求△PMN的面积；
②若2＜S_△PMN＜6，结合函数的图象，直接写出n的取值范围．

查看试题解析
27. 如图，在正方形ABCD中，E是边AB上一动点（不与A、B重合），连接DE，交对角线AC于点F，过点F作DE的垂线分别交AD、BC于点M、N．

(1)、根据题意，补全图形；

(2)、证明：FD＝FN；

(3)、直接写出BN和AF的数量关系．

查看试题解析
28. 在平面直角坐标系xOy中的点 $P (x_{1} ， y_{1}) ， Q (x_{2} ， y_{2})$ ，给出如下定义：若 $| x_{1} - x_{2} | \leq | y_{1} - y_{2} |$ ，则d（P，Q）＝ $| x_{1} - x_{2} |$ ；若 $| x_{1} - x_{2} | > | y_{1} - y_{2} |$ ，则d（P，Q）＝ $| y_{1} - y_{2} |$ ．

(1)、已知点A（1，2），B（3，2），则d（O，A）＝， d（O，B）＝；

(2)、点C坐标（m，n），且d（O，C）＝1．
①当mn＜0时，写出一个符合条件的点C的坐标　 ▲ 　；

②所有符合条件的点C所组成的图形记作W，在图1中画出图形W；

(3)、如图2，矩形DEFG中，D（﹣1，0），E（3.5，0），F（3.5，2.5），M（3，2）是矩形内部一点，N是矩形边上的点，且d（M，N）≥1，若直线y＝kx+4上存在点N，直接写出k的取值范围．

查看试题解析

x	3.23	3.24	3.25	3.26
ax²+bx+c	﹣0.06	﹣0.02	0.03	0.09