人教版八年级数学期中测试题(16~18章)
试卷更新日期:2022-04-11 类型:期中考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 且 D、 且2. 下列运算正确的是( )A、 B、 C、 D、3. 已知a= ,b= ,则a与b的关系是( )A、相等 B、互为相反数 C、互为倒数 D、平方值相等4. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A、9,40,41 B、5,12,13 C、0.3,0.4,0.5 D、8,24,255. 要焊接一个如图所示的钢架,需要的钢材长度是( )
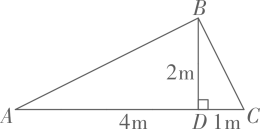 A、 B、 C、 D、6. 我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( )
A、 B、 C、 D、6. 我国古代算书《九章算术》中第九章第六题是:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深葭长各几何?你读懂题意了吗?请回答水深______尺,葭长_____尺.解:根据题意,设水深OB=x尺,则葭长OA'=(x+1)尺.可列方程正确的是( ) A、x2+52 =(x+1)2 B、x2+52 =(x﹣1)2 C、x2+(x+1)2 =102 D、x2+(x﹣1)2=527. 在 ▱ABCD中, ,则 等于( )A、 B、 C、 D、8. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( )
A、x2+52 =(x+1)2 B、x2+52 =(x﹣1)2 C、x2+(x+1)2 =102 D、x2+(x﹣1)2=527. 在 ▱ABCD中, ,则 等于( )A、 B、 C、 D、8. 如图,在四边形ABCD中,对角线AC和BD相交于点O,下列条件不能判定四边形ABCD是平行四边形的是( ) A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD
A、AB∥DC,AD∥BC B、AB= DC,AD=BC C、AB∥DC,AD=BC D、OA=OC,OB=OD二、填空题
-
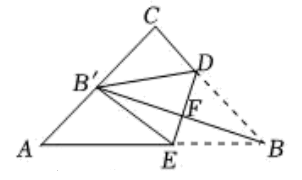
9. 计算:(-3)(+3)=.10. 化简 的结果是.11. 已知, ,当x分别取1,2,3,…,2021时,所对应的y值的总和是.12. 如图,在等腰中, , .点和点分别在边和边上,连接.将沿折叠,得到 , 点恰好落在的中点处.设与交于点 , 则.
 13. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.
13. 如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上OA=5;OC=4.在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处.则D坐标为.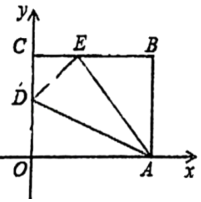 14. 如图,在四边形ABCD中,∠BAD=∠BCD=45°,AB= ,CD=5,AD=7,则BC= , AC=.
14. 如图,在四边形ABCD中,∠BAD=∠BCD=45°,AB= ,CD=5,AD=7,则BC= , AC=. 15. 在四边形ABCD中,对角线AC,BD交于点O,OA=OC=OB=OD,添加一个条件使四边形ABCD是正方形,那么所添加的条件可以是(写出一个即可)16. 如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
15. 在四边形ABCD中,对角线AC,BD交于点O,OA=OC=OB=OD,添加一个条件使四边形ABCD是正方形,那么所添加的条件可以是(写出一个即可)16. 如图,一个正方形摆放在桌面上,那么这个正方形的边长为 .
三、计算题
-
17. 若x , y为实数,且y= + + .求 - 的值.18. 计算:(1)、 ;(2)、 .
四、解答题
-
19. 实数a,b在数轴上的位置如图所示,化简.
 20. 在一个边长为()cm的正方形内部挖去一个边长为()cm的正方形(如图所示),求剩余阴影部分图形的面积.
20. 在一个边长为()cm的正方形内部挖去一个边长为()cm的正方形(如图所示),求剩余阴影部分图形的面积. 21. 如图所示的一块空地进行草坪绿化,已知 AD=4m ,CD=3m,AD⊥DC,AB=13m ,BC=12m ,绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱.
21. 如图所示的一块空地进行草坪绿化,已知 AD=4m ,CD=3m,AD⊥DC,AB=13m ,BC=12m ,绿化草坪价格 150 元/米2。求这块地草坪绿化的价钱.
 22. 如图,有一直角三角形纸片,两直角边AB=6cm,AC=8cm,现将直角边AB沿直线BD进行对折,使点A刚好落在斜边BC上,且与A'B重合,求BD的长,
22. 如图,有一直角三角形纸片,两直角边AB=6cm,AC=8cm,现将直角边AB沿直线BD进行对折,使点A刚好落在斜边BC上,且与A'B重合,求BD的长,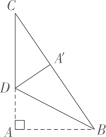 23. 用反证法证明下列问题。
23. 用反证法证明下列问题。如图,在△ABC中,点D,E分别在AC,AB上,BD,CE相交于点O。

求证:BD和CE不可能互相平分。
24. 如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.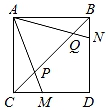 25. 在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的.
25. 在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的. (1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):
(1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取 ,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
(3)、(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且 , ,设 ,试用含 的代数式表示DF的长.