广西壮族自治区柳州市三江侗族自治县2020-2021学年九年级下学期期中数学试卷

试卷更新日期：2022-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. $- \frac{1}{2021}$ 的倒数是（）

A、 $\frac{1}{2021}$ B、-2021 C、 $- \frac{1}{2021}$ D、2021

查看试题解析
2. 下列运算正确的是（）

A、a²•a³＝a⁶ B、 $\sqrt{a^{2}} = a$ C、 $(a + b)^{2} = a^{2} + b^{2}$ D、（a³＋1）（a³﹣1）＝a⁶﹣1

查看试题解析
3. 已知一组数据：66，66，62，68，63，这组数据的平均数和中位数分别是（）

A、66，62 B、65，66 C、65，62 D、66，66

查看试题解析
4. 新型冠状病毒的平均直径约为0.00000012m，用科学记数法表示该数据为（）

A、1.2×10^﹣⁸ B、1.2×10^﹣⁷ C、12×10^﹣⁸ D、1.2×10⁷

查看试题解析
5. 下列四个银行标志中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
6. 已知正三角形外接圆半径为 $\sqrt{3}$ ，这个正三角形的边长是（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
7. 如图，BD∥AC，BE平分∠ABD，交AC于点E．若∠A=50°，则∠1的度数为（）

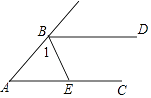A、65° B、60° C、55° D、50°

查看试题解析
8.
如图，已知AB是⊙O的直径，∠D=40°，则∠CAB的度数为（　　）

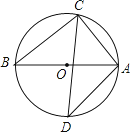A、20° B、40° C、50° D、70°

查看试题解析
9. 如图是用若干个全等的等腰梯形拼成的图形，下列说法错误的是（）

A、梯形的下底是上底的两倍 B、梯形最大角是 $120 °$ C、梯形的腰与上底相等 D、梯形的底角是 $60 °$

查看试题解析
10. 已知 $a^{2} + b^{2} = 6 a b$ ，且a>b>0，则 $\frac{a + b}{a - b}$ 的值为（）

A、 $\sqrt{2}$ B、± $\sqrt{2}$ C、2 D、±2

查看试题解析
11. 如图，在▱ABCD中，AB＝6，AD＝9，∠BAD的平分线交BC于点E ，交DC的延长线于点F ， BG⊥AE ，垂足为G ， BG＝ $4 \sqrt{2}$ ，则△CEF的周长为（）

A、8 B、9.5 C、10 D、11.5

查看试题解析
12. 已知：二次函数y＝ax²＋bx＋c（a≠0）的图象如图所示，下列结论中：①abc＞0；②2a＋b＜0；③a－b＋c＜0；④当x＞1时，y随x的增大而增大；⑤a＞1，其中正确的项是（）

A、①②⑤ B、①④⑤ C、①③⑤ D、②③④

查看试题解析

二、填空题

13. 若关于x的一元二次方程 $x^{2} - 4 x + k = 0$ 有两个相等的实数根，则k的值为.

查看试题解析
14. 函数 $y = \frac{\sqrt{x + 1}}{x}$ 有意义，则自变量 $x$ 的取值范围是.

查看试题解析
15. 小明在离路灯底部6 $m$ 处测得自己的影子长为1.2 $m$ ，小明的身高为1.6 $m$ ，那么路灯的高度为 $m$ .

查看试题解析
16. 如图，函数 $y_{1} = x - 1$ 和函数 $y_{2} = \frac{2}{x}$ 的图象相交于点 $M (2 ， m)$ ， $N (- 1 ， n)$ ，若 $y_{1} > y_{2}$ ，则x的取值范围是.

查看试题解析
17. 如图是一个高速公路隧道的横截面，若它的形状是以O为圆心的圆的一部分，路面AB=8米，净高CD=8米，则此圆的半径OA为.

查看试题解析
18. 规定： $s i n (- α) = - s i n α ， c o s (- α) = c o s α$ ， $s i n (α + β) = s i n α c o s β + c o s α s i n β$ ，据此判断下列等式成立的是：.（写出所有正确的序号）
①cos（﹣60°）＝ $- \frac{1}{2}$ ， ②sin75°＝ $\frac{\sqrt{6} + \sqrt{2}}{4}$ ， ③ $s i n 2 α = 2 s i n α c o s α$ ， ④ $s i n (α - β) = s i n α c o s β - c o s α s i n β$

查看试题解析

三、解答题

19. 计算： $- 2^{3} \times 2^{- 2} + \sqrt{18} + t a n 4 5^{∘} - (4 s i n 6 0^{∘} + 1)^{0} - | 2 - 3 \sqrt{2} |$ .

查看试题解析
20. 已知分式： $A = \frac{2}{x^{2} - 1}$ ， $B = \frac{1}{x + 1} + \frac{1}{1 - x}$ . $(x \neq \pm 1)$ .下面三个结论：① $A$ ， $B$ 相等，② $A$ ， $B$ 互为相反数，③ $A$ ， $B$ 互为倒数，请问哪个正确？为什么？

查看试题解析
21. 如图，在方格纸上，以格点连线为边的三角形叫做格点三角形，请按要求完成下列
操作：
先将格点△ABC绕A点逆时针旋转90°得到△A₁B₁C₁ ，再将△A₁B₁C₁沿直线B₁C₁作轴反射得到△A₂B₂C₂.

查看试题解析
22. 某校为了庆祝建国七十周年，决定举办一台文艺晚会，为了了解学生最喜爱的节目形式，随机抽取了部分学生进行调查，规定每人从“歌曲”，“舞蹈”，“小品”，“相声”和“其它”五个选项中选择一个，并将调查结果绘制成如下两幅不完整的统计图表，请根据图中信息，解答下列题：

最喜爱的节目

人数

歌曲

15

舞蹈

a

小品

12

相声

10

其它

b

(1)、在此次调查中，该校一共调查了名学生；

(2)、a＝；b＝；

(3)、在扇形计图中，计算“歌曲”所在扇形的圆心角的度数；

(4)、若该校共有1200名学生，请你估计最喜爱“相声”的学生的人数．

查看试题解析
23. 我市某生态果园今年收获了 $15$ 吨李子和 $8$ 吨桃子，要租用甲、乙两种货车共 $6$ 辆，及时运往外地，甲种货车可装李子 $4$ 吨和桃子 $1$ 吨，乙种货车可装李子 $1$ 吨和桃子 $3$ 吨.

(1)、共有几种租车方案？

(2)、若甲种货车每辆需付运费 $1000$ 元，乙种货车每辆需付运费 $700$ 元，请选出最佳方案，此方案运费是多少.

查看试题解析
24. 如图，已知反比例函数 $y = \frac{k_{1}}{x}$ $(k_{1} > 0)$ 与一次函数 $y = k_{2} x + 1$ $(k_{2} \neq 0)$ 相交于 $A$ 、 $B$ 两点， $A C ⊥ x$ 轴于点 $C$ .若 $Δ O A C$ 的面积为 $1$ ，且 $t a n ∠ A O C = 2$ .

(1)、求出反比例函数与一次函数的解析式；

(2)、请直接写出 $B$ 点的坐标，并指出当 $x$ 在什么范围取值时，使 $\frac{k_{1}}{x} - (k_{2} x + 1) > 0$

查看试题解析
25. 如图， $Δ A B C$ 内接于⊙O，且 $A B$ 为⊙O的直径， $O E ⊥ A B$ 交 $A C$ 于点 $E$ ，在 $O E$ 的延长线上取点 $D$ ，使得∠DCE＝∠B.

(1)、求证： $C D$ 是⊙O的切线；

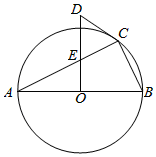(2)、若 $A C = 2 \sqrt{5}$ ， $B C = \sqrt{5}$ ，求AE的长.

查看试题解析
26. 如图，在平面直角坐标系中，O为坐标原点，抛物线y＝ax²＋bx＋c（a≠0）过O、B、C三点，B、C坐标分别为（10，0）和（ $\frac{18}{5}$ ， ﹣ $\frac{24}{5}$ ），以OB为直径的⊙A经过C点，直线l垂直x轴于B点.

(1)、求直线BC的解析式；

(2)、求抛物线解析式及顶点坐标；

(3)、点M是⊙A上一动点（不同于O，B），过点M作⊙A的切线，交y轴于点E，交直线l于点F，设线段ME长为m，MF长为n，请猜想m•n的值，并证明你的结论；

(4)、若点P从O出发，以每秒一个单位的速度向点B作直线运动，点Q同时从B出发，以相同速度向点C作直线运动，经过t（0＜t≤8）秒时恰好使△BPQ为等腰三角形，请求出满足条件的t值.

查看试题解析

最喜爱的节目	人数
歌曲	15
舞蹈	a
小品	12
相声	10
其它	b