浙江省绍兴市诸暨市浣东教育共同体2020-2021学年七年级下学期期中数学试卷

试卷更新日期：2022-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $2021^{0}$ 的结果是（）

A、2021 B、1 C、0 D、 $\frac{1}{2021}$

查看试题解析
2. 随着微电子制造技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占0.0000007（平方毫米），这个数用科学记数法表示为（）

A、 $7 \times 1 0^{7}$ B、 $7 \times 1 0^{- 7}$ C、 $0.7 \times 1 0^{- 6}$ D、 $70 \times 1 0^{- 8}$

查看试题解析
3. 若 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是方程 $3 x + a y = 1$ 的一个解，则a的值是（）

A、 $1$ B、 $- 1$ C、 $2$ D、 $- 2$

查看试题解析
4. 如图，将三角板与直尺贴在一起，使三角板的直角顶点C（ $∠ A C B = 90 °$ ）在直尺的一边上，若 $∠ 2 = 55 °$ ，则 $∠ 1$ 的度数是（）

A、15° B、25° C、35° D、65°

查看试题解析
5. 将方程3x﹣y＝1变形为用x的代数式表示y（　　）

A、3x＝y+1 B、x＝ $\frac{1 + y}{3}$ C、y＝1﹣3x D、y＝3x﹣1

查看试题解析
6. 已知 $a^{m} = 2$ ， $a^{n} = 4$ ，则 $a^{3 m - 2 n} =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $1$ D、 $2$

查看试题解析
7. 某车间有56名工人，每人每天能生产螺栓16个或螺母24个，设有x名工人生产螺栓，y名工人生产螺母，每天生产的螺栓和螺母按1：2配套，下面所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 56 \\ 2 \times 16 x = 24 y \end{array}$ B、 ${\begin{array}{l} x + y = 56 \\ 2 \times 24 x = 16 y \end{array}$ C、 ${\begin{array}{l} x + y = 28 \\ 16 x = 25 y \end{array}$ D、 ${\begin{array}{l} x + y = 36 \\ 24 x = 16 y \end{array}$

查看试题解析
8. 如图，AB∥CD，用含∠1，∠2，∠3的式子表示∠4，则∠4的值为（　　）

A、∠1+∠2﹣∠3 B、∠1+∠3﹣∠2 C、180°+∠3﹣∠1﹣∠2 D、∠2+∠3﹣∠1﹣180°

查看试题解析
9. 杨辉是我国南宋时期杰出的数学家和教育家，如图是杨辉在公元1261年著作《解：九章算法》里面的一张图，即“杨辉三角”.它是古代重要的数学成就，比西方的“帕斯卡三角形”早了300多年.请仔细观察计算该图中第n行中所有数字之和为（）

A、2n^﹣² B、2n^﹣¹ C、2n D、2n⁺¹

查看试题解析
10. 现有一列数： $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， …， $a_{n - 1}$ ， $a_{n}$ （为正整数），规定 $a_{1} = 2$ ， $a_{2} - a_{1} = 4$ ， $a_{3} - a_{2} = 6$ ， …， $a_{n} - a_{n - 1} = 2 n (n \geq 2)$ ， $\frac{1}{a_{2}} + \frac{1}{a_{3}} + \frac{1}{a_{4}} + ⋯ ⋯ + \frac{1}{a_{2021}}$ 的值为（）

A、 $\frac{502}{1009}$ B、 $\frac{503}{1011}$ C、 $\frac{505}{1011}$ D、 $\frac{504}{1009}$

查看试题解析

二、填空题

11. 计算： $x y (x - y) =$ .

查看试题解析
12. 如图，已知直线 $l_{1}$ ， $l_{2}$ 被l $3$ 所截， $l_{1} / / l_{2}$ ， $∠ 2 = 125 °$ ，则 $∠ 1 =$ .

查看试题解析
13. 若3 $x^{2 m - 3}$ － $y^{2 n - 1}$ =5是二元一次方程，则 $m$ = ， $n$ =.

查看试题解析
14. 如图把三角板的直角顶点放在直线b上，若∠1=40°，则当∠2=度时，a∥b.

查看试题解析
15. 如图，把一张长方形纸条ABCD沿EF折叠，若∠BGD'为x度，则∠1的度数应为度(用含x的代数式表示)。

查看试题解析
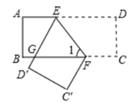16. 一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来的方向上平行前进，若第一次向左拐40°，则第二次向右拐的角度是度.

查看试题解析
17. 已知方程组 ${\begin{array}{l} 2 a - 3 b = c_{1} \\ 3 a + 5 b = c_{2} \end{array}$ 的解是 ${\begin{array}{l} a = 8.3 \\ b = 1.2 \end{array}$ 利用这一结果，观察、比较可知方程组 ${\begin{array}{l} 2 (x - 1) - 3 (y + 1) = c_{1} \\ 3 (x - 1) + 5 (y + 1) = c_{2} \end{array}$ 的解为.

查看试题解析
18. 已知 ${(x - 2)}^{x - 2021} = 1$ ，则x＝.

查看试题解析

三、解答题

19. 计算

(1)、 $3 \times (- \frac{1}{42})^{0} - \sqrt{16} + (\frac{1}{2})^{- 1}$

(2)、 $(- 2 a^{3})^{2} \cdot 3 a^{3} + 6 a^{12} \div (- 2 a^{3})$ ，

查看试题解析
20. 解方程组

(1)、 ${\begin{array}{l} 3 x - 2 y = - 1 \\ x - y = 1 \end{array}$

(2)、 ${\begin{array}{l} 2 x + 3 y = 4 \\ 5 x - 3 y = 19 \end{array}$

查看试题解析
21. 先化简，再求值： $(m - 2) (m^{2} + 2 m + 4) - 2 m (m^{2} - 3)$ ，其中 $m = - 2$

查看试题解析
22. 如图，在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

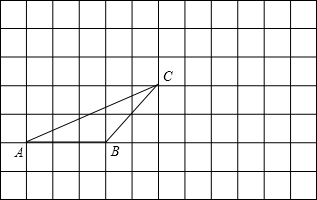
① 过点A画出BC的平行线；
② 画出先将△ABC向右平移5格，再向上平移3格后的△DEF．

查看试题解析
23. 已知：如图，在△ABC中，点D、E分别在BC、AC上，且AB∥DE，∠1＝∠2．
求证：AF∥BC．

查看试题解析
24. 已知方程组 ${\begin{array}{l} 4 x - y = 5 \\ a x + b y = - 1 \end{array}$ 和 ${\begin{array}{l} 3 x + y = 9 \\ 3 a x + 4 b y = 18 \end{array}$ 有相同的解，求 ${(2 a + 3 b)}^{2021}$ 的值.

查看试题解析
25. 确保室内空气新鲜一方面是提高生活质量的需要，另一方面也是有效防控新型冠状病毒传播的需要，因而越来越多的居民选购家用空气净化器以净化室内空气.阳光商场抓住商机，从厂家购进了A、B两种型号的净化器共140台，A型号净化器进价是900元/台，B型号净化器进价是2100元/台，购进两种型号净化器共用去174000元.

(1)、求商场各进了A、B两种型号的净化器多少台？

(2)、为使每台B型号净化器的毛利润是A型号的2倍，且保证售完这140台净化器的毛利润达到54000元，求每台A型号净化器的售价.（注：毛利润＝售价—进价）

查看试题解析
26. 在矩形 $A B C D$ 内，将两张边长分别为a和b（ $a > b$ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的周长为 $c_{1}$ ，图2中阴影部分的周长为 $c_{2}$ .

(1)、当 $A B = 4$ ， $A D = 6$ 时，分别求出 $c_{1}$ ， $c_{2}$ 的值.（用含a，b的代数式表示，结果需化简）

(2)、小明在计算时发现，若 $A D - A B = 3$ ，矩形ABCD的面积为 $\frac{27}{4}$ 那么就能求出矩形 $A B C D$ 的周长，请你帮他完成.

查看试题解析