浙江省宁波市江北区2020-2021学年七年级下学期期中数学试卷

试卷更新日期：2022-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. 下列现象中，不属于平移的是（）

A、滑雪运动员在的平坦雪地上滑行 B、钟摆的摆动 C、大楼上上下下地迎送来客的电梯 D、火车在笔直的铁轨上飞驰而过

查看试题解析
2. 目前发现的新冠病毒其直径约为 $0.00012$ 毫米，则这个数字用科学记数法表示正确的是（）

A、 $1.2 \times 1 0^{4}$ B、 $1.2 \times 1 0^{- 4}$ C、 $0.12 \times 1 0^{5}$ D、 $0.12 \times 1 0^{- 5}$

查看试题解析
3. 下列运算正确的是（）

A、a²•b³=a⁶ B、（a²）⁵=a⁷ C、（﹣3b）²=6b² D、a³÷a²=a

查看试题解析
4. 下列命题中，真命题是（）

A、相等的角是对顶角 B、两条直线被第三条直线所截，同位角相等 C、在同一平面内，垂直于同一条直线的两条直线平行 D、同旁内角互补

查看试题解析
5. 下列不能进行平方差计算的是（）

A、(x+y)(-x-y) B、（2a+b）(2a-b) C、(-3x-y)(-y+3x) D、（a²+b）(a²-b)

查看试题解析
6. 某公司用3000元购进两种货物，货物卖出后，一种货物的利润率是10%，另一种货物的利润率是11%，两种货物共获利315元，如果设该公司购进这两和货物所用的费用分别为x元，y元，则列出的方程组是（）

A、 ${\begin{array}{l} x + y = 3315 \\ x (1 + 10 %) + y (1 + 11 %) = 315 \end{array}$ B、 ${\begin{array}{l} x + y = 3315 \\ 10 % x + 11 % y = 315 \end{array}$ C、 ${\begin{array}{l} x + y = 3000 \\ x (1 + 10 %) + y (1 + 11 %) = 315 \end{array}$ D、 ${\begin{array}{l} x + y = 3000 \\ 10 % x + 11 % y = 315 \end{array}$

查看试题解析
7. 下列图形中，∠1和∠2不是同位角的是（　　）

A、 B、 C、 D、

查看试题解析
8. 已知多项式x﹣a与x²+2x﹣b的乘积中不含x²项，则常数a的值是（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
9. 将一张矩形纸片折叠成如图所示的图形，若 $∠ C A B = 30^{°}$ ，则 $∠ A C B$ 的度数是（）

A、 $45^{°}$ B、 $55^{°}$ C、 $65^{°}$ D、 $75^{°}$

查看试题解析
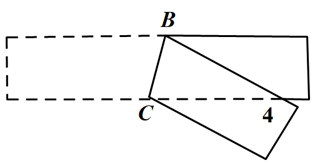10. 如图，已知AB∥EG，BC∥DE，CD∥EF，则x、y、z三者之间的关系是（）

A、x+y+z＝180° B、x﹣z＝y C、y﹣x＝z D、y﹣x＝x﹣z

查看试题解析

二、填空题

11. $3^{- 1}$ ＝.

查看试题解析
12. 请写一个二元一次方程组，使它的解是 ${\begin{cases} x = 2 \\ y = - 2 \end{cases}$ ．

查看试题解析
13. 将方程 $3 x + y = 7$ 变形成用含y的代数式表示 $x ：$ .

查看试题解析
14. 如果一个角的两边分别与另一个角的两边平行，若其中一个角为40°，则另一个角为.

查看试题解析
15. 计算： $59.8 \times 60.2 =$ .

查看试题解析
16. 若多项式9x²+mx+1是一个完全平方式，则m＝.

查看试题解析
17. 若 $(1 - x)^{2 - 3 x}$ ＝1，则x＝.

查看试题解析
18. 已知关于x，y的方程组 ${\begin{array}{l} a x - b y = 13 \\ c x + d y = 30.9 \end{array}$ 的解为 ${\begin{array}{l} x = 8.3 \\ y = 1.2 \end{array}$ ，则关于x，y的方程组 ${\begin{array}{l} a (x + 2) - b y + b = 13 \\ c (x + 2) + d y - d = 30.9 \end{array}$ 的解为：.

查看试题解析

三、解答题

19. 计算：

(1)、2⁰+（ $\frac{1}{2}$ ）^﹣¹；

(2)、（2a）²+（a³﹣a）÷a.

查看试题解析
20. 解下列方程组：

(1)、 ${\begin{array}{l} y = 4 x - 13 \\ 3 x + 2 y = 7 \end{array}$ ；

(2)、 ${\begin{array}{l} 2 x + 3 y = - 4 \\ 2 x - 3 y = 8 \end{array}$ .

查看试题解析
21. 先化简，再求值：（2x+3）（2x﹣3）+（x﹣2）²﹣3x（x﹣1），其中x＝2.

查看试题解析
22. 如图，∠1=70°，∠2=110°，∠C=∠D，试探索∠A与∠F有怎样的数量关系，并说明理由．

查看试题解析
23. 已知实数a，b满足（a+b）²＝9，（a﹣b）²＝3，求a²+b²﹣ab的值.

查看试题解析
24. 阅读下列材料：.
（材料一）“a²≥0“这个结论在数学中非常有用，有时我们需要将代数式配成完全平方式.例如：x²+4x+5＝x²+4x+4+1＝（x+2）²+1，
∵（x+2）²≥0，∴（x+2）²+1≥1，∴x²+4x+5≥1.
（材料二）我们在比较两个数或式大小的时候常用“作差法“.
例如：若a﹣b＞0，则a＞b；若a﹣b＝0，则a＝b；若a﹣b＜0，则a＜b.
试利用上述阅读材料解决下列问题：

(1)、填空：x²﹣6x+10＝（x）²+；

(2)、已知x²﹣2xy+2y²+2y+1＝0，则x+y的值为；

(3)、比较代数式x²﹣1与2x﹣3的大小，并说明理由.

查看试题解析
25. 某商场计划用56000元从厂家购进60台新型电子产品，已知该厂家生产甲乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入x，y台，其中每台的价格、销售获利如下表：

甲型

乙型

丙型

价格(元/台)

1000

800

500

销售获利(元/台)

260

190

120

(1)、购买丙型设备台(用含x，y的代数式表示)；

(2)、若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了56000元，则商场有哪几种购进方案？

(3)、在第(2)题的基础上，为了使销售时获利最多，应选择哪种购进方案？此时获利为多少？

查看试题解析

	甲型	乙型	丙型
价格(元/台)	1000	800	500
销售获利(元/台)	260	190	120