浙江省宁波市北仑区精准联盟2020-2021学年七年级下学期期中数学试卷

试卷更新日期：2022-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，属于二元一次方程的是（）

A、 ${\begin{cases} x = 1 \\ y = 5 \end{cases} ， {\begin{cases} x = 4 \\ y = 3 \end{cases} ， {\begin{cases} x = 7 \\ y = 1 \end{cases}$ B、 $y = x - 1$ C、 $x + \frac{1}{x} = 2$ D、 $x^{2} - 2 x + 1 = 0$

查看试题解析
2. 下列各图案中，是由一个基本图形通过平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 已知：如图，直线a，b被直线c所截，且a//b，若∠1=70°，则∠2的度数是（）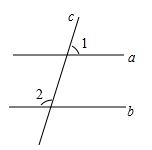

A、110° B、130° C、80° D、70°

查看试题解析
4. 下列运算正确的是（）

A、（ab）⁵＝ab⁵ B、a⁸•a²＝a¹⁰ C、（a²）³＝a⁵ D、（a﹣b）²＝a²﹣b²

查看试题解析
5. 如图，下列条件中，不能判断直线a//b的是（）

A、∠1=∠3 B、∠2+∠4=180° C、∠4=∠5 D、∠2=∠3

查看试题解析
6. 下列因式分解正确的是（　　）

A、a²+8ab+16b²=（a+4b）² B、a⁴﹣16=（a²+4）（a²﹣4） C、4a²+2ab+b²=（2a+b）² D、a²+2ab﹣b²=（a﹣b）²

查看试题解析
7. 若方程组 ${\begin{array}{l} x + 2 y = 1 \\ (k - 1) x + (k + 1) y = 2 \end{array}$ 的解x与y相等，则k的值为（）

A、3 B、2 C、1 D、不能确定

查看试题解析
8. 若x²+2（2p﹣3）x+4是完全平方式，则p的值等于（）

A、 $\frac{5}{2}$ B、2 C、2或1 D、 $\frac{5}{2}$ 或 $\frac{1}{2}$

查看试题解析
9. 小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路，她去学校共用了16分钟，假设小颖上坡路的平均速度是3千米/小时，下坡路的平均速度是5千米/小时，若设小颖上坡用了 $x \min$ ，下坡用了 $y \min$ ，根据题意可列方程组（）

A、 ${\begin{array}{l} 3 x + 5 y = 1200 \\ x + y = 16 \end{array}$ B、 ${\begin{array}{l} \frac{3}{60} x + \frac{5}{60} y = 1.2 \\ x + y = 16 \end{array}$ C、 ${\begin{array}{l} 3 x + 5 y = 1.2 \\ x + y = 16 \end{array}$ D、 ${\begin{array}{l} \frac{3}{60} x + \frac{5}{60} y = 1200 \\ x + y = 16 \end{array}$

查看试题解析
10. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）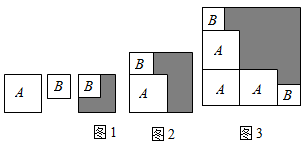

A、22 B、24 C、42 D、44

查看试题解析

二、填空题

11. 某种病毒的直径是0.00000008米，这个数据用科学记数法表示为米。

查看试题解析
12. 计算：（15x³y⁵﹣10x⁴y⁴﹣20x³y²）÷（﹣5x³y²）＝.

查看试题解析
13. 已知二元一次方程 $5 x - 7 y = 4$ ，用 $x$ 的代数式表示 $y$ ，则 $y =$ .

查看试题解析
14. 若 $2 x + y - 2 = 0$ ，则 $5^{2 x} \cdot 5^{y} =$ .

查看试题解析
15. 某公园“6·1”期间举行特优读书游园活动，成人票和儿童票均有较大折扣.张凯、李利都随他们的家人参加了本次活动.王斌也想去，就去打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩，共花了38元钱；李利说他家去了4个大人和2个小孩，共花了44元钱.王斌家计划去3个大人和2个小孩，请你帮他计算一下，需准备元钱买门票.

查看试题解析
16. 我国古代数学家杨辉发现了如图所示的三角形，我们称之为“杨辉三角”，从图中取一列数：1，3，6，10，…，记 $a_{1} = 1$ ， $a_{2} = 3$ ， $a_{3} = 6$ ， $a_{4} = 10$ ，…，那么 $a_{4} + a_{11} - 2 a_{10} + 10$ 的值是．

查看试题解析

三、解答题

17. 计算：

(1)、（ $\sqrt{3}$ ）⁰﹣（ $\frac{1}{2}$ ）^﹣³+（﹣3）²；

(2)、（ $\frac{1}{3}$ xy）²•（﹣12x²y²）÷（﹣ $\frac{4}{3}$ x³y）.

查看试题解析
18. 因式分解：

(1)、3x²y²z﹣27y⁴z；

(2)、（a²+1）²﹣4a².

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} 4 x - 8 y = - 20 \\ 3 x + y = 13 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 (m + n) - 4 (m - n) = 4 \\ \frac{m + n}{2} + \frac{m - n}{6} = 1 \end{array}$ .

查看试题解析
20. 先化简再求值

(1)、 $\frac{1}{2} (3 a + 2 b)^{2} - a (\frac{3}{2} a - 2 b)$ ，其中 $a = 1 ， b = 2$ .

(2)、已知 $y^{2} - 5 y + 3 = 0$ ，求 $2 (y - 1) (2 y - 1) - 2 (y + 1)^{2} + 7$ 的值.

查看试题解析
21. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．

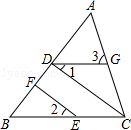(1)、CD与EF平行吗？请说明理由．

(2)、如果∠1=∠2，且∠3=60°，求∠ACB的度数．

查看试题解析
22. 从边长为a的正方形中剪掉一个边长为b的正方形（如图①），然后将剩余部分拼成一个长方形（如图②）.

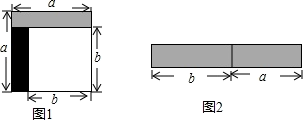(1)、上述操作能验证的等式是；

(2)、应用你从（1）得出的等式，完成下列各题：
①已知x²−4y²=12，x+2y=4，求x−2y的值.

②计算：（1− $\frac{1}{2^{2}}$ ）（1− $\frac{1}{3^{2}}$ ）（1− $\frac{1}{4^{2}}$ ）…（1− $\frac{1}{1 9^{2}}$ ）（1− $\frac{1}{2 0^{2}}$ ）.

查看试题解析
23. 水果市场将120吨水果运往各地商家，现有甲、乙、丙三种车型供选择，每辆车的运载能力和运费如表所示：（假设每辆车均满载）
车型
甲
乙
丙
汽车运载量（吨/辆）
5
8
10
汽车运费（元/辆）
400
500
600

(1)、若全部水果都用甲、乙两种车型来运送，需运费8200元，问分别需甲、乙两种车型各几辆？

(2)、为了节约运费，市场可以调用甲、乙、丙三种车型参与运送（每种车型至少1辆），已知它们的总辆数为16辆，如何安排车辆运送使总运费最省？

查看试题解析
24. 已知 $P Q / / M N$ ，将一副三角板中的两块直角三角板如图1放置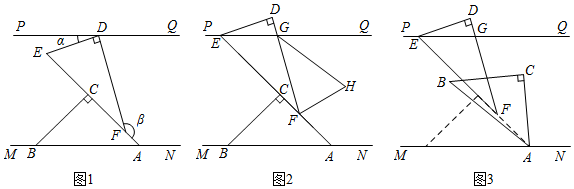， $∠ A C B = ∠ E D F = 90 °$ ， $∠ A B C = ∠ B A C = 45 °$ ， $∠ D F E = 30 °$ ， $∠ D E F = 60 °$ .

(1)、若三角板如图1摆放时，则 $∠ α =$ ， $∠ β =$ .

(2)、现固定 $△ A B C$ 的位置不变，将 $△ D E F$ 沿 $A C$ 方向平移至点E正好落在 $P Q$ 上，如图2所示， $D F$ 与 $P Q$ 交于点G，作 $∠ F G Q$ 和 $∠ G F A$ 的角平分线交于点H，求 $∠ G H F$ 的度数；

(3)、现固定 $△ D E F$ ，将 $△ A B C$ 绕点A顺时针旋转至 $A C$ 与直线 $A N$ 首次重合的过程中，当线段 $B C$ 与 $△ D E F$ 的一条边平行时，请直接写出 $∠ B A M$ 的度数.

查看试题解析

车型	甲	乙	丙
汽车运载量（吨/辆）	5	8	10
汽车运费（元/辆）	400	500	600