人教版七年级数学下册期中测试题（5~8章）

试卷更新日期：2022-04-11 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示， $∠ A O B$ 是平角， $O C$ 是射线， $O D$ 、 $O E$ 分别是 $∠ A O C$ 、 $∠ B O C$ 的角平分线，若 $∠ C O E = 28 °$ ，则 $∠ A O D$ 的度数为（）

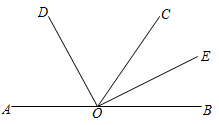A、56° B、62° C、72° D、124°

查看试题解析
2. 如图，直线AB，CD相交于点O，∠AOE＝90°，∠DOF＝90°，OB平分∠DOG，给出下列结论：
①当∠AOF＝60°时，∠DOE＝60°；②OD为∠EOG的平分线；③与∠BOD相等的角有三个；④∠COG＝∠AOB﹣2∠EOF.其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
3. 下面四个图形中，∠1与∠2是对顶角的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各数中，不是无理数的是（）

A、π B、0.1010010001… C、 $\sqrt{2}$ D、3

查看试题解析
5. 实数 $\frac{π}{4}$ ，0， $\sqrt[3]{27}$ ， $\sqrt{7}$ ， $\frac{\sqrt{16}}{2}$ ，0.1，-0.313313331…（每两个1之间依次增加一个3），其中无理数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 以下点在第二象限的是（）

A、（0，0） B、（3，﹣5） C、（﹣5，8） D、（﹣2，﹣1）

查看试题解析
7. 在平面直角坐标系xOy中，点A（﹣2，0），点B（0，3），点C在坐标轴上，若三角形ABC的面积为6，则符合题意的点C有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，雷达探测器测得六个目标A，B，C，D，E，F出现，按照规定的目标表示方法，目标C，F的位置分别表示为C（6，120°），F（5，210°），按照此方法在表示目标A，B，D，E的位置时，其中表示不正确的是（）

A、A（5，30°） B、B（2，90°） C、D（4，240°） D、E（3，60°）

查看试题解析
9. 若关于x，y的方程组 ${\begin{array}{l} x + 2 y = 2 k \\ 4 x - y = 5 k \end{array}$ 的解x，y满足x-y=1，则k的值为（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

10. 如图，已知EF⊥AB，∠1=26°，则当AB∥CD时，∠2=.

查看试题解析
11. 如图， $∠ A O B = 40^{°} ， O C$ 平分 $∠ A O B$ ，直尺与OC垂直，则 $∠ 1 =$ .

查看试题解析
12. 已知：x-2的平方根是±2， $2 x + y + 7$ 的立方根为3，则 $x^{2} + y^{2}$ 的算术平方根为.

查看试题解析
13. 若 $^{3} \sqrt{a}$ =-5，则a= ．

查看试题解析
14. 若 $\sqrt{{(3 - x)}^{2}}$ =x-3成立，则x需满足条件：.

查看试题解析
15. 已知点 P（ a + 5 ， a -1 ）在第四象限，且到 x 轴的距离为 2，则点 P的坐标为．

查看试题解析
16. 已知点A（1，4），B（0，2），C（4，0），则△ABC的周长为．

查看试题解析

三、计算题

17. 选择适合的方法解下列方程组.

(1)、 ${\begin{array}{l} 3 x + 7 y = 9 ， ① \\ 4 x - 7 y = 5. ② \end{array}$

(2)、 ${\begin{array}{l} x + 2 (x + 2 y) = 4 ， ① \\ x + 2 y = 2. ② \end{array}$

查看试题解析
18. 计算：

(1)、（1﹣ $\sqrt{3}$ ）×（2+ $\sqrt{12}$ ）；

(2)、 $\sqrt{13^{2} - 12^{2}} - \sqrt[3]{- 27}$ +（3﹣ $\sqrt{3}$ ）（3+ $\sqrt{3}$ ）．

查看试题解析

四、解答题

19. 已知 $A D ⊥ B C ， F G ⊥ B C$ ，垂足分別为点D，G，且 $∠ 1 = ∠ 2 ， ∠ C = 50^{°}$ ，求 $∠ E D C$ 的度数.

查看试题解析
20. 已知，如图，CD平分∠ACB， $D E ∥ B C$ ，∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程，请在括号内填上恰当的依据.

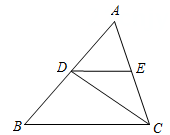
证明： $D E ∥ B C$ （已知）

∴∠ACB=∠AED（   ）

∠EDC=∠DCB（   ）

又∵CD平分∠ACB（已知）

∴ $∠ D C B = \frac{1}{2} ∠ A C B$ （   ）

又∵∠AED=82°（已知）

∴∠ACB=82°（   ）

∴ $∠ D C B = \frac{1}{2} \times 82 ° = 41 °$ ，

∴∠EDC=∠DCB=41°（   ）

查看试题解析
21. 已知x+1的平方根是±2，2x+y﹣2的立方根是2，求x²+y²的算术平方根．

查看试题解析
22. 若无理数A的整数部分是a，则它的小数部分可表示为A-a．例如：π的整数部分是3，因此其小数部分可表示为π-3．若x表示 $\sqrt{47}$ 的整数部分，y表示它的小数部分，求代数式( $\sqrt{47}$ +x)y的值．

查看试题解析
23. 画出以A（0，0），B（3，0）， C（5，4）， D（2，4）为顶点的四边形ABCD，并求其面积.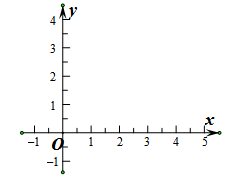

查看试题解析
24. 直线EF、GH之间有一个直角三角形ABC，其中∠BAC=90°，∠ABC=α。

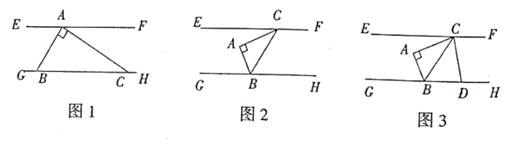(1)、如图1，点A在直线EF上，B、C在直线GH上，若∠α=60°，∠FAC=30°。试说明：EF∥GH；

(2)、将三角形ABC如图2放置，直线EF∥GH，点C、B分别在直线EF、GH上，且BC平分∠ABH。求∠ECA的度数；(用α的代数式表示)

(3)、在(2)的前提下，直线CD平分∠FCA交直线GH于D，如图3，在α取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化请求出变化的范围。

查看试题解析
25. 2021年下半年，新冠疫情在全球新一波蔓延，接种新冠疫苗是当前抗击疫情最有效的手段.某县注射的疫苗有两种，一种是2针剂的灭活疫苗，另种是3针剂的重组蛋白疫苗.某校120名教职工全部完成其中一种疫苗的注射，共注射了325针，注射2针剂和3针剂疫苗的教职工各有多少人?

查看试题解析