（人教版）2021-2022学年度第二学期第七章平面直角坐标系7.2 坐标方法的简单应用期中复习卷
试卷更新日期：2022-04-11 类型：复习试卷
一、单选题
-
1. 小明在介绍郑州外国语中学位置时，相对准确的表述为（ ）A、陇海路以北 B、工人路以西 C、郑州市人民政府西南方向 D、陇海路和工人路交叉口西北角2. 小嘉去电影院观看《长津湖》，如果用(5，7)表示5排7座，那么小嘉坐在7排8座可表示为（ )A、(5，7) B、(7，8） C、(8，7) D、(T，5)3. 在下列说法中，能确定位置的是（ ）A、禅城区季华五路 B、中山公园与火车站之间 C、距离祖庙300米 D、金马影剧院大厅5排21号4. 根据下列表述，能够确定一点位置的是（ ）A、东北方向 B、尚志中学报告厅第8排 C、永和西路 D、地图上东经20度北纬30度5. 岚山根——袁家村·运城印象全民健身游乐场，位处运城市黄金旅游路线上，南靠中条山，东临九龙山，西临凤凰谷和死海景区，是运城盐湖区全域旅游中项目最全，规模最大的标志性综合游乐场（图1）．若利用网格（图2）建立适当的平面直角坐标系，表示冲浪乐园的点的坐标为 ，表示特色小吃米线的坐标为 ，那么儿童游乐园所在的位置 的坐标应是（ ）
A、 B、 C、 D、6. 在大型爱国主义电影《长津湖》中，我军缴获了敌人防御工程的坐标地图碎片（如图），若一号暗堡坐标为(1，2)，四号暗堡坐标为(－3，2)，指挥部坐标为(0，0)，则敌人指挥部可能在（ ）
A、A处 B、B处 C、C处 D、D处7. 在平面直角坐标系xOy中，点A（﹣2，0），点B（0，3），点C在坐标轴上，若三角形ABC的面积为6，则符合题意的点C有（ ）A、1个 B、2个 C、3个 D、4个8. 在平面直角坐标系中，已知点A (－1，1)， B(－3，2)，点C在坐标轴上，若△ABC是等腰三角形，则满足条件的点C的个数是（ ）A、4个 B、5个 C、7个 D、8个9. 矩形的三个顶点坐标分别是(-2，-3)，(1，-3)，(-2，-4)，那么第四个顶点坐标是（ ）A、(1，-4) B、(-8，-4) C、(1，-3) D、(3，-4)10. 在平面直角坐标系坐标中，第二象限内的点A到x轴的距离是3，到y轴的距离是2，则A点坐标为（ ）A、（﹣3，2） B、（﹣2，3） C、（2，﹣3） D、（3，﹣2）二、填空题
-
11. 如图所示，一方队正沿箭头所指的方向前进， A的位置为三列四行（排），表示为（3，4），那么B左侧第二个人的位置是
12. 将如图所示的“ ”笑脸放置在 的正方形网格中， 、 、 三点均在格点上.若 、 的坐标分别为 ， ，则点 的坐标为.
13. 电影票上“10排3号”，记作 ，“8排23号”，记作 ，则“5排16号”记作.14. 如图，在平面直角坐标系中，点A和B的坐标分别为（2，0），（0，-4），若将线段AB绕点A顺时针旋转90°得到线段AC，则点C的坐标为
15. 如图，在平面直角坐标系中， ，点B，C的坐标分别是 ， ，则点A的坐标是.
三、解答题
-
16. 下图是某市旅游景点示意图，请建立适当的坐标系，写出各景点的坐标；
17. 如图所示，某班教室有9排5列座位．
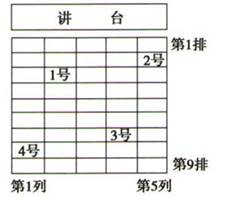
1号同学说：“小明在我的右后方．
2号同学说：“小明在我的左后方．”
3号同学说：“小明在我的左前方．”
4号同学说：“小明与1号同学和3号同学的距离一样远．”
根据上面4位同学的描述，试确定“5号”小明的位置．
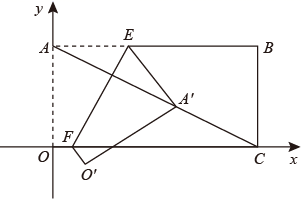
18. 十一期间，小明一家一起去旅游，如图是小明设计的某旅游景点的图纸（网格是由相同的小正方形组成的，且小正方形的边长代表实际长度100m，在该图纸上可看到两个标志性景点A，B若建立适当的平面直角坐标系，则点A（－3，1），B（－3，－3），第三个景点C（1，3）的位置已破损。
(1)、请在图中画出平面直角坐标系，并标出景点C的位置；(2)、平面直角坐标系的坐标原点为点O，△ACO是直角三角形吗？请判断并说明理由.19. 如图，矩形OABC中，AO＝4，AB＝8，点E，F分别在边AB，OC上，且AE＝3，将矩形的部分沿直线EF翻折，点A的对应点A'恰好落在对角线AC上，求OF的长.
为矩形，以点 
为原点建立直角坐标系，点 
在 
轴的负半轴上，点 
在 
轴的正半轴上，已知点 
坐标为( 
2，4)，反比例函数 图象经过 BC 的中点 
，且与 AB 交于点 
．
的值； 
为 ，求 的解析式； 