(人教版)2021-2022学年度第二学期第五章相交线与平行线期中复习卷
试卷更新日期:2022-04-10 类型:复习试卷
一、单选题
-
1. 如图l1∥l2点О在直线l1上,将三角板的直角顶点放在点О处,三角板的两条直角边与l2交于A,B两点,若∠1=35°,则∠2的度数为( )
 A、35° B、45° C、55° D、65°2. 如图,在 中, , ,观察图中尺规作图的痕迹,可知 的度数为( )
A、35° B、45° C、55° D、65°2. 如图,在 中, , ,观察图中尺规作图的痕迹,可知 的度数为( ) A、40° B、50° C、55° D、60°3. 如图,直线b、c被直线a所截,则与是( )
A、40° B、50° C、55° D、60°3. 如图,直线b、c被直线a所截,则与是( ) A、对顶角 B、同位角 C、内错角 D、同旁内角4. 下列图形中,∠1和∠2不是同位角的是( )A、
A、对顶角 B、同位角 C、内错角 D、同旁内角4. 下列图形中,∠1和∠2不是同位角的是( )A、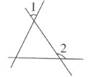 B、
B、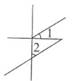 C、
C、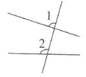 D、
D、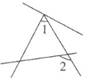 5. 下列命题宜用反证法证明的是( )A、等腰三角形两腰上的高相等 B、有一个外角是120°的等腰三角形是等边三角形 C、在同一平面内,若两条直线都与第三条直线平行,则这两条直线互相平行 D、全等三角形的面积相等6. 如图所示,AB∥CD,E为AB上方一点,FB, HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150° ,则∠EFG的度数为( )
5. 下列命题宜用反证法证明的是( )A、等腰三角形两腰上的高相等 B、有一个外角是120°的等腰三角形是等边三角形 C、在同一平面内,若两条直线都与第三条直线平行,则这两条直线互相平行 D、全等三角形的面积相等6. 如图所示,AB∥CD,E为AB上方一点,FB, HG分别为∠EFG,∠EHD的角平分线,若∠E+2∠G=150° ,则∠EFG的度数为( ) A、90° B、95° C、100° D、150°7. 如图所示, ,有下列结论:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,则 .其中正确的有( )
A、90° B、95° C、100° D、150°7. 如图所示, ,有下列结论:①若 ,则 ;②若 ,则 ;③若 ,则 ;④若 ,则 .其中正确的有( ) A、1个 B、2个 C、3个 D、4个8. 下列图形中,根据∠1=∠2,能得到AB∥CD的是( )A、
A、1个 B、2个 C、3个 D、4个8. 下列图形中,根据∠1=∠2,能得到AB∥CD的是( )A、 B、
B、 C、
C、 D、
D、 9. 下列命题正确的是( )A、三角形的内切圆圆心到三角形三个顶点的距离相等 B、对角线互相垂直平分的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、顺次连接四边形各边中点所得四边形是平行四边形10. 如图,在▱ABCD中,对角线AC,BD相交于点O,将△AOB平移至△DPC的位置,连结OP,则图中平行四边形的个数为( )
9. 下列命题正确的是( )A、三角形的内切圆圆心到三角形三个顶点的距离相等 B、对角线互相垂直平分的四边形是矩形 C、有一组邻边相等的四边形是菱形 D、顺次连接四边形各边中点所得四边形是平行四边形10. 如图,在▱ABCD中,对角线AC,BD相交于点O,将△AOB平移至△DPC的位置,连结OP,则图中平行四边形的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,点P是直线l外一点,从点P向直线l引 , , , 几条线段,其中只有线段与直线l垂直.这几条线段中,的长度最短.
 12. 如图所示,木工师傅用角尺画平行线a,b的依据是。
12. 如图所示,木工师傅用角尺画平行线a,b的依据是。 13. 如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为 .
13. 如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为 . 14. 数轴上点A表示的数是 ,将点A在数轴上平移5个单位长度得到点B.则点B表示的数是.15. 如图,与 是内错角的是.
14. 数轴上点A表示的数是 ,将点A在数轴上平移5个单位长度得到点B.则点B表示的数是.15. 如图,与 是内错角的是.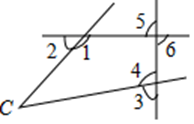
三、解答题
-
16. 如图,已知∠1=∠2 求证:a∥b.
 17. 如图, 平分 ,求 和 的度数.
17. 如图, 平分 ,求 和 的度数. 18. 完成下面的证明:
18. 完成下面的证明:已知:如图,∠1=30°,∠B=60°,AB⊥AC.求证:AD∥BC.

证明:∵AB⊥AC(已知)
∴∠ ▲ =90°( ▲ )
∵∠1=30°,∠B=60°(已知)
∴∠1+∠BAC+∠B= ▲ ( ▲ )
即∠ ▲ +∠B=180°
∴AD∥BC( ▲ )
19. 如图,已知AB∥CD,∠A=60°,∠ECD=120°,求∠ECA的度数.

