（人教版）2021-2022学年度第二学期第五章相交线与平行线5.3平行线的性质期中复习卷
试卷更新日期：2022-04-10 类型：复习试卷
一、单选题
-
1. 如图，已知直线m∥n，线段AB的两个端点A，B分别落在直线m，n上，将线段AB绕点A按逆时针方向旋转80°得到线段AC，连结BC.若∠1＝30°，则∠2的度数为（ ）
A、15° B、20° C、25° D、30°2. 如图，AB∥CD，点P为CD上一点，PF是∠EPC的平分线，若∠1=55°，则∠EPD的大小为（ ）
A、60° B、70° C、80° D、100°3. 如图，直线AB∥CD，CD∥EF，且∠B=30°，∠CGE=125°，则∠CGB的度数为（ ）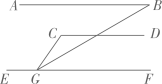
A、45° B、40° C、30° D、25°4. 如图，在▱ABCD中，AE平分∠BAD且交BC于点E，∠D=58°，则∠AEC的大小是 （ ）
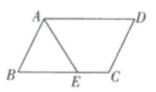A、61° B、109° C、119° D、122°5. 下列命题是假命题的是（ ）A、同位角相等 B、三角形内角和是180° C、内错角相等，两直线平行 D、三角形的一个外角大于任何一个和它不相邻的内角6. 下列命题是假命题的是（ ）A、等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合 B、若 ，则 C、角平分线上的点到这个角两边的距离相等 D、若 是直角三角形，则其三边长a、b、c满足：7. 已知命题"关于 的一元二次方程 ，当 时必有实数解”，能说明这个命题是假命题的一个反例可以是（ ）A、 B、 C、 D、8. 数学中说明某个命题不成立时常采用“举反例”，即举一个满足条件，但不满足结论的例子.为说明命题“对于任何实数a，都有 ＝a”是假命题，所列举反例正确的是（ ）A、a＝﹣2 B、a＝ C、a＝1 D、a＝9. 如图，a∥b，一个直角三角形的一个顶点落在其中一条直线上，若∠1=78°，则∠2的度数为（ ）
A、12° B、15° C、25° D、30°10. 如图，直线AB//CD，则下列结论中正确的是（ ）
A、∠1=∠2 B、∠3=∠4 C、∠1+∠3=180° D、∠3＋∠4=180°二、填空题
-
11. 如图，在Rt△ABC中，AB＝4，BC＝3，点D在斜边AB上，连接CD把△ACD沿直线CD翻折，使点A落在同一平面内的点A′处.当A′D与Rt△ABC的直角边垂直时，AD的长为 .
12. 如图，在△ABC中，AB=AC，D为BC上的一点，∠BAD=28°，在AD的右侧作△ACE，使得AE=AD，∠DAE=∠BAC，连接CE，DE，DE交AC于点O，若CE∥AB，则∠DOC的度数为
13. 如图，已知平行四边形ABCD中，∠BCD的平分线交边AD于E，∠ABC的平分线交AD于F，CD＝10，AE＝4，则EF＝.
14. 命题“两个全等三角形的周长相等”的逆命题是.15. 小豪发现一个命题：“如果两个无理数 ， ， 满足 ， 那么这两个无理数的和是无理数．”这个命题是（填写“真命题”，“假命题”）；请你举例说明 ．三、解答题
-
16. 如图，在△ABC中，∠A=48°，CE是∠ACB的平分线，B、C、D在同一直线上，DF∥CE，∠D=40°，求∠B的度数．
17. 如图，∠C=90°，点D是CB的中点，将△ACD沿AD折叠后得到△AED，过点B作BF∥AC交AE的延长线于点F.求证：BF=EF.
18. 已知，如图，CD平分∠ACB， ，∠AED=82°.求∠EDC的度数.下面是小明同学的证明过程，请在括号内填上恰当的依据.
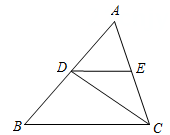
证明： （已知）
∴∠ACB=∠AED（ ）
∠EDC=∠DCB（ ）
又∵CD平分∠ACB（已知）
∴ （ ）
又∵∠AED=82°（已知）
∴∠ACB=82°（ ）
∴ ，
∴∠EDC=∠DCB=41°（ ）
19. 已知，如图，∠ACB＝60°，∠ABC＝50°，BO、CO分别平分∠ABC、∠ACB，EF是经过点O且平行于BC的直线，求∠BOC的度数.
20. 写出命题“如果一个角的两边与另一个角的两边分别垂直，那么这两个角相等”的逆命题，并判断原命题和逆命题的真假．若是假命题，请举出反例．
