2022年中考数学二轮专题复习-相似三角形
试卷更新日期:2022-04-09 类型:二轮复习
一、单选题
-
1. 若 且相似比为1:4,则 与 的面积比为( )A、1:4 B、4:1 C、1:16 D、16:12. 如图,D是BC上的点,∠ADC=∠BAC,则下列结论正确的是( )
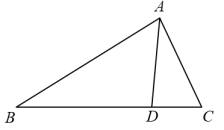 A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对3. 如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )
A、△ABC∽△DAB B、△ABC∽△DAC C、△ABD∽△ACD D、以上都对3. 如图,△ABO∽△CDO,若BO=8,DO=4,CD=3,则AB的长是( )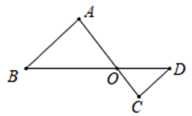 A、2 B、3 C、4 D、64. 如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,并测得 , , 那么树DB的高度是( )
A、2 B、3 C、4 D、64. 如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2m,并测得 , , 那么树DB的高度是( )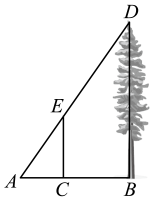 A、6m B、8m C、32m D、25m5. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A、6m B、8m C、32m D、25m5. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )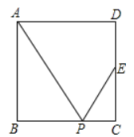 A、 B、 C、是的中点 D、6. 如图,在正方形ABCD中,E是边BC上一点,且BE:CE=1:3,DE交AC于点F,若DE=10,则CF等于( )
A、 B、 C、是的中点 D、6. 如图,在正方形ABCD中,E是边BC上一点,且BE:CE=1:3,DE交AC于点F,若DE=10,则CF等于( ) A、 B、 C、 D、7. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A、 B、 C、 D、7. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( ) A、3:4:7 B、9:16:49 C、9:21:49 D、3:7:498. 如图, 与 是以坐标原点O为位似中心的位似图形,若点A是 的中点, 的面积是6,则 的面积为( )
A、3:4:7 B、9:16:49 C、9:21:49 D、3:7:498. 如图, 与 是以坐标原点O为位似中心的位似图形,若点A是 的中点, 的面积是6,则 的面积为( ) A、9 B、12 C、18 D、249. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )
A、9 B、12 C、18 D、249. 如图,在平面直角坐标系中,将 以原点O为位似中心放大后得到 ,若 , ,则 与 的面积的比是( )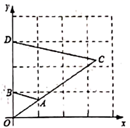 A、 B、 C、 D、10. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )
A、 B、 C、 D、10. 如图,在 ABC中,DE BC,EF AB,下列等式成立的是( )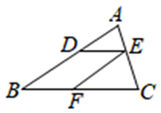 A、 B、 C、 D、11. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )
A、 B、 C、 D、11. 直角三角形中, , 三个正方形如图放置,边长分别为 , , , 已知 , , 则的值为( )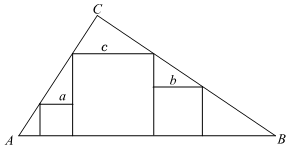 A、4 B、 C、5 D、612. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm.
A、4 B、 C、5 D、612. 如图,矩形ABCD中,AB=8cm,AD=6cm,EF是对角线BD的垂直平分线,则EF的长为( )cm. A、 B、5 C、 D、813. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A、 B、5 C、 D、813. 如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )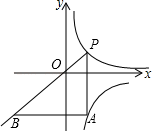 A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案14. 如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1 , △AEB的面积为S2 , 当 = 时,则 的值是( )
A、逐渐变大或变小 B、等于定值16 C、等于定值8 D、另有答案14. 如图△ACB,∠ACB=90°,点O是AB的中点,CD平分∠BCO交AB于点D,作AE⊥CD分别交CO、BC于点G,E. 记△AGO的面积为S1 , △AEB的面积为S2 , 当 = 时,则 的值是( )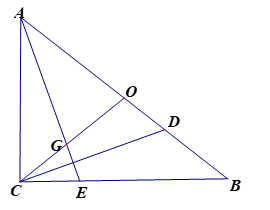 A、 B、 C、 D、15. 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
A、 B、 C、 D、15. 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )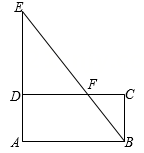 A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( )
A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( ) A、 B、 C、 D、17. 如图,正方形ABCD中,点E是边CD上的动点(不与点C、D重合),以CE为边向右作正方形CEFG,连接AF,点H是AF的中点,连接DH、CH.下列结论:①△ADH≌△CDH;②AF平分∠DFE;③若BC=4,CG=3,则AF=5;④若 , 则 . 其中正确的有( )
A、 B、 C、 D、17. 如图,正方形ABCD中,点E是边CD上的动点(不与点C、D重合),以CE为边向右作正方形CEFG,连接AF,点H是AF的中点,连接DH、CH.下列结论:①△ADH≌△CDH;②AF平分∠DFE;③若BC=4,CG=3,则AF=5;④若 , 则 . 其中正确的有( )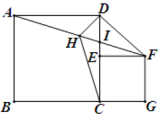 A、1个 B、2个 C、3个 D、4个18. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( )
A、1个 B、2个 C、3个 D、4个18. 如图,中, , , , , 为 , 边上的两个动点,且 , 为中点,则的最小值为( ) A、 B、 C、 D、19. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )
A、 B、 C、 D、19. 如图,矩形纸片 , , 点 , 分别在 , 上,把纸片如图沿折叠,点 , 的对应点分别为A' , B' , 连接并延长交线段于点 , 则的值为( )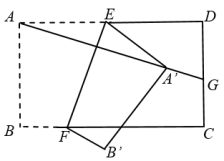 A、 B、 C、 D、20. 如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合), , 分别表示四边形和的面积,则的最大值是( )
A、 B、 C、 D、20. 如图,是的重心,过的一条直线分别与AB、AC相交于G、H(均不与的顶点重合), , 分别表示四边形和的面积,则的最大值是( )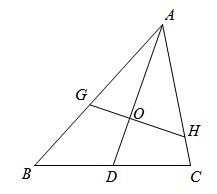 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
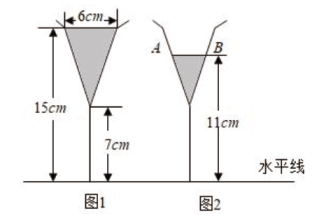
21. 若 , , 的面积为 ,则 的面积为 .22. 若D为中边上一点,且EDBC交于E, , 若与的相似比为 , 则.23. 图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面AB= cm
 24. 如图,中, , 点、、分别在、、上,且四边是正方形.若 , , , , 则.
24. 如图,中, , 点、、分别在、、上,且四边是正方形.若 , , , , 则.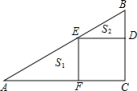 25. 如图,小明为了测量高楼MN的高度,在离点N18米的点A处放了一个平面镜,小明沿NA方向后退1.5米到点C ,此时从镜子中恰好看到楼顶的点M,已知小明的眼睛(点B)到地面的高度BC是1.6米,则高楼MN的高度是.
25. 如图,小明为了测量高楼MN的高度,在离点N18米的点A处放了一个平面镜,小明沿NA方向后退1.5米到点C ,此时从镜子中恰好看到楼顶的点M,已知小明的眼睛(点B)到地面的高度BC是1.6米,则高楼MN的高度是.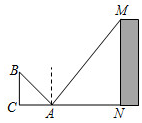 26. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .
26. 如图,矩形ABCD的顶点A、B分别在反比例函数与的图象上,点C、D在x轴上,AB、BD分别交y轴于点E、F,则阴影部分的面积为 .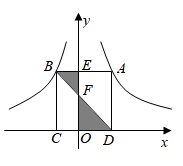 27. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有.
27. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=4S△ADF.其中正确的有.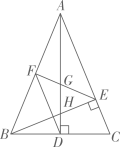 28. 如图,点A在线段BD上,在BD的同侧作等腰直角 和等腰直角 ,CD与BE、AE分别交于点P,M.对于下列结论:① ;② ;③ ;④ ;其中正确的结论有.(写出所有正确结论的序号)
28. 如图,点A在线段BD上,在BD的同侧作等腰直角 和等腰直角 ,CD与BE、AE分别交于点P,M.对于下列结论:① ;② ;③ ;④ ;其中正确的结论有.(写出所有正确结论的序号)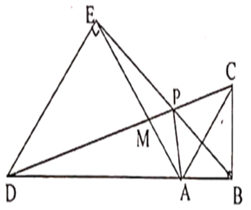 29. 在菱形中, , , , 相交于点 . 将一个足够大的直角三角板60°角的顶点放在菱形的顶点处,绕点左右旋转,其中三角板60°角的两边分别与边 , 相交于点 , , 连接与相交于点 . 旋转过程中,当点为边的四等分点时(), .
29. 在菱形中, , , , 相交于点 . 将一个足够大的直角三角板60°角的顶点放在菱形的顶点处,绕点左右旋转,其中三角板60°角的两边分别与边 , 相交于点 , , 连接与相交于点 . 旋转过程中,当点为边的四等分点时(), .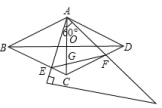 30. 如图,Rt△ABC,∠ACB=90°,AC=BC=3,以C为顶点的正方形CDEF(C、D、E、F四个顶点按逆时针方向排列)可以绕点C自由转动,且CD=2,连接AF,BD,在正方形CDEF旋转过程中,BD+AD的最小值为.
30. 如图,Rt△ABC,∠ACB=90°,AC=BC=3,以C为顶点的正方形CDEF(C、D、E、F四个顶点按逆时针方向排列)可以绕点C自由转动,且CD=2,连接AF,BD,在正方形CDEF旋转过程中,BD+AD的最小值为.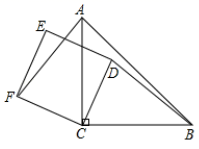
三、计算题
-
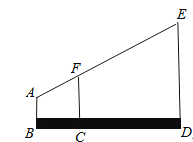
31. 如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.
 32. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.
32. 如图,矩形ABCD中,AD=3,AB=4,点P是对角线AC上一动点(不与A,C重合),连结BP,作PE⊥PB,交射线DC于点E,以线段PE,PB为邻边作矩形BPEF.过点P作GH⊥CD,分别交AB、CD于点G、H.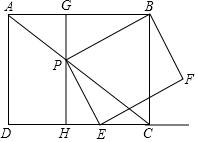 (1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.
(1)、求证:△PGB∽△EHP;(2)、求 的值;(3)、求矩形BPEF的面积的最小值.四、解答题
-
33. 某校初三年级在一次研学活动中,数学研学小组为了估计澧水河某段水域的宽度,在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C ,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE BC.经测量BC=25米,BD=12米,DE=35米,求河的宽度AB为多少米?
 34. 如图,在△ACB中,AC=30cm,BC=25cm.动点P从点C出发,沿CA向终点A匀速运动,速度是2cm/s;同时,动点Q从点B出发,沿BC向终点C匀速运动,速度是1cm/s.当△CPQ与△CAB相似时,求运动的时间.
34. 如图,在△ACB中,AC=30cm,BC=25cm.动点P从点C出发,沿CA向终点A匀速运动,速度是2cm/s;同时,动点Q从点B出发,沿BC向终点C匀速运动,速度是1cm/s.当△CPQ与△CAB相似时,求运动的时间.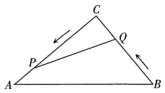 35. 如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
35. 如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.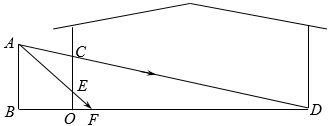 36. 如图
36. 如图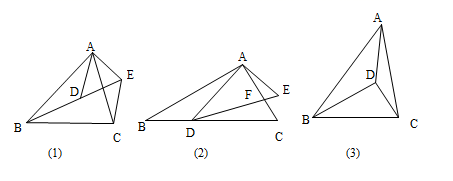
问题背景如图(1),已知 ,求证: ;
尝试应用如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值(提示;连接 );
拓展创新如图(3), 是 内一点, , , , ,直接写出 的长.
37. 已知:△ABC与△ABD中,∠CAB=∠DBA=β,且∠ADB+∠ACB=180°.
提出问题:如图1,当∠ADB=∠ACB=90°时,求证:AD=BC;
类比探究:如图2,当∠ADB≠∠ACB时,AD=BC是否还成立?并说明理由.
综合运用:如图3,当β=18°,BC=1,且AB⊥BC时,求AC的长.
38. 如图,在矩形ABCD中,AD=4,DC=3,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿C→O→B运动.到点B停止,点Q沿A→D→C运动,到点C停止.连接AP、AQ、PQ,设△APQ的面积为y(cm2)(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s). (1)、填空:BO=cm;(2)、当PQ∥CD时,求x的值;(3)、当 时,求y与x之间的函数关系式;(4)、直接写出在整运动过程中,使AQ=PQ的所有x的值.
(1)、填空:BO=cm;(2)、当PQ∥CD时,求x的值;(3)、当 时,求y与x之间的函数关系式;(4)、直接写出在整运动过程中,使AQ=PQ的所有x的值.五、综合题
-
39. 如图1,⊙O的弦BC=6,A为BC所对优弧上一动点且 , 的外角平分线AP交⊙O于点P,直线AP与直线BC交于点E.
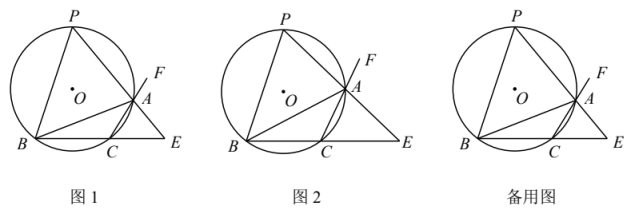 (1)、求证:点P为的中点;(2)、如图2,求⊙O的半径和PC的长;(3)、若不是锐角三角形,求的最大值.40. 如图,在直角坐标系中,直线 与 轴、 轴的交点分别为 、 ,以 为对称轴的抛物线 与 轴分别交于点 、 .
(1)、求证:点P为的中点;(2)、如图2,求⊙O的半径和PC的长;(3)、若不是锐角三角形,求的最大值.40. 如图,在直角坐标系中,直线 与 轴、 轴的交点分别为 、 ,以 为对称轴的抛物线 与 轴分别交于点 、 .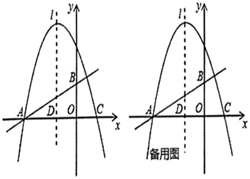 (1)、求抛物线的解析式;(2)、若点 是第二象限内抛物线上的动点,其横坐标为 .设抛物线的对称轴 与 轴交于点 ,连接 ,交 于 ,求出当以 、 、 为顶点的三角形与 相似时点 的坐标;(3)、点 是对称轴上任意一点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、若点 是第二象限内抛物线上的动点,其横坐标为 .设抛物线的对称轴 与 轴交于点 ,连接 ,交 于 ,求出当以 、 、 为顶点的三角形与 相似时点 的坐标;(3)、点 是对称轴上任意一点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,说明理由.