2022年中考数学二轮专题复习-矩形、菱形及正方形
试卷更新日期:2022-04-09 类型:二轮复习
一、单选题
-
1. 下列四边形中,对角线互相垂直平分的是( )A、平行四边形、菱形 B、矩形、菱形 C、矩形、正方形 D、菱形、正方形2. 下列测量方案中,能确定四边形门框为矩形的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量对角线是否相等 D、测量对角线交点到四个顶点的距离是否都相等3. 如图,菱形 的对角线 、 相交于点 ,过点 作 于点 ,连接 ,若 , ,则菱形 的面积为( )
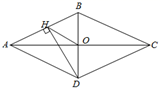 A、 B、 C、 D、4. 如图,有甲、乙、丙三个矩形,其中相似的是( )
A、 B、 C、 D、4. 如图,有甲、乙、丙三个矩形,其中相似的是( )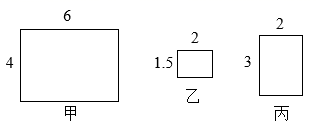 A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似5. 如图,在菱形ABCD中,DE⊥AB,cosA= , AE=3,则tan∠DBE的值是( )
A、甲与丙 B、甲与乙 C、乙与丙 D、三个矩形都不相似5. 如图,在菱形ABCD中,DE⊥AB,cosA= , AE=3,则tan∠DBE的值是( ) A、 B、2 C、 D、6. 如图,在菱形ABCD中,对角线AC与BD交于点O,E是边AB的中点,连结OE.若菱形ABCD的面积为24,AC=8,则OE的长为( )
A、 B、2 C、 D、6. 如图,在菱形ABCD中,对角线AC与BD交于点O,E是边AB的中点,连结OE.若菱形ABCD的面积为24,AC=8,则OE的长为( ) A、 B、3 C、 D、57. 如图,在正方形ABCD中,E是边BC上一点,且BE:CE=1:3,DE交AC于点F,若DE=10,则CF等于( )
A、 B、3 C、 D、57. 如图,在正方形ABCD中,E是边BC上一点,且BE:CE=1:3,DE交AC于点F,若DE=10,则CF等于( ) A、 B、 C、 D、8. 如图,矩形中,对角线交于点O, , 则矩形的面积是( )
A、 B、 C、 D、8. 如图,矩形中,对角线交于点O, , 则矩形的面积是( ) A、2 B、 C、 D、89. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
A、2 B、 C、 D、89. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )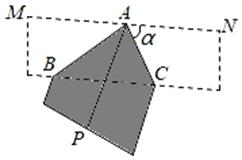 A、 cm2 B、(36 )cm2 C、 cm2 D、 cm210. 如图所示,反比例函数 的图象经过矩形OABC的边AB的中点 ,则矩形OABC的面积为( )
A、 cm2 B、(36 )cm2 C、 cm2 D、 cm210. 如图所示,反比例函数 的图象经过矩形OABC的边AB的中点 ,则矩形OABC的面积为( ) A、2 B、4 C、5 D、811. 如图,在菱形ABCD中, AB=4,∠B=60°,AE⊥BC,AF⊥CD ,垂足分别为点E,F,连结EF,则 △AEF 的面积是( )
A、2 B、4 C、5 D、811. 如图,在菱形ABCD中, AB=4,∠B=60°,AE⊥BC,AF⊥CD ,垂足分别为点E,F,连结EF,则 △AEF 的面积是( )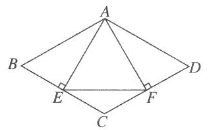 A、 B、 C、 D、12. 如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF的长为( )
A、 B、 C、 D、12. 如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF的长为( )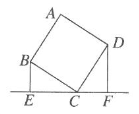 A、6.5dm B、6dm C、5.5dm D、4dm13. 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )
A、6.5dm B、6dm C、5.5dm D、4dm13. 将一矩形纸片ABCD沿CE折叠,B点恰好落在AD边上的F处,若 ,则 的值为( )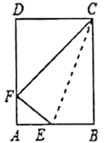 A、 B、 C、 D、14. 正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为( )
A、 B、 C、 D、14. 正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上的一动点,DN+MN的最小值为( ) A、6 B、8 C、10 D、915. 如图,在矩形ABCD中,对角线、BD交于C, , 垂足为E, , 那么的面积是( )
A、6 B、8 C、10 D、915. 如图,在矩形ABCD中,对角线、BD交于C, , 垂足为E, , 那么的面积是( ) A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( )
A、 B、 C、 D、16. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( ) A、 B、 C、 D、17. 如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )
A、 B、 C、 D、17. 如图,正方形 的边长为a,点E在边 上运动(不与点A,B重合), ,点F在射线 上,且 与 相交于点G,连接 .则下列结论:① ,② 的周长为 ,③ ;④当 时,G是线段 的中点,其中正确的结论是( )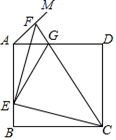 A、①②③ B、①④ C、①③④ D、①②③④18. 如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,AC与EF相交于点G,若 , ,则FG的长为( )
A、①②③ B、①④ C、①③④ D、①②③④18. 如图,菱形ABCD的边长为4,E、F分别是AB、AD上的点,AC与EF相交于点G,若 , ,则FG的长为( ) A、 B、2 C、3 D、419. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边分别作正方形BAHI,正方形BCFG与正方形CADE,延长BG,FG分别交AD,DE于点K,J,连结DH,IJ.图中两块阴影部分面积分别记为S1 , S2.若S1:S2=1:4,S四边形边BAHE=18,则四边形MBNJ的面积为( )
A、 B、2 C、3 D、419. 如图,在△ABC中,∠ACB=90°,以△ABC的各边为边分别作正方形BAHI,正方形BCFG与正方形CADE,延长BG,FG分别交AD,DE于点K,J,连结DH,IJ.图中两块阴影部分面积分别记为S1 , S2.若S1:S2=1:4,S四边形边BAHE=18,则四边形MBNJ的面积为( ) A、5 B、6 C、8 D、920. 如图,在Rt△ABC中,∠CBA=60°,斜边AB=10,分别以△ABC的三边长为边在AB上方作正方形,S1 , S2 , S3 , S4 , S5分别表示对应阴影部分的面积,则S1+S2+S3+S4+S5=( )
A、5 B、6 C、8 D、920. 如图,在Rt△ABC中,∠CBA=60°,斜边AB=10,分别以△ABC的三边长为边在AB上方作正方形,S1 , S2 , S3 , S4 , S5分别表示对应阴影部分的面积,则S1+S2+S3+S4+S5=( ) A、50 B、50 C、100 D、100
A、50 B、50 C、100 D、100二、填空题
-
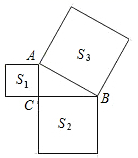
21. 在四边形ABCD中,对角线AC,BD交于点O,OA=OC=OB=OD,添加一个条件使四边形ABCD是正方形,那么所添加的条件可以是(写出一个即可)22. 如图, 分别以Rt△ABC三边构造三个正方形,面积分别为S1 , S2 , S3 , 若S1=15,S3=39,则S2=.
 23. 如图,在平面直角坐标系中,点A1(1,0)、A2(3,0)、A3(6,0)、A4(10,0)、……,以A1A2为对角线作第一个正方形A1C1A2B1 , 以A2A3为对角线作第二个正方形A2C2A3B2 , 以A3A4 , 为对角线作第三个正方形A3C3A4B3 , ……,顶点B1 , B2 , B3……都在第一象限,按照此规律依次下去,则点Bn的坐标为.
23. 如图,在平面直角坐标系中,点A1(1,0)、A2(3,0)、A3(6,0)、A4(10,0)、……,以A1A2为对角线作第一个正方形A1C1A2B1 , 以A2A3为对角线作第二个正方形A2C2A3B2 , 以A3A4 , 为对角线作第三个正方形A3C3A4B3 , ……,顶点B1 , B2 , B3……都在第一象限,按照此规律依次下去,则点Bn的坐标为.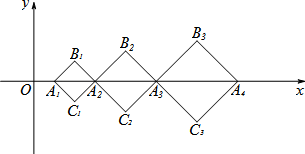 24. 如图,菱形ABCD的对角线 ,BD相交于点 , , ,以AB为直径作一个半圆,则图中阴影部分的面积为.
24. 如图,菱形ABCD的对角线 ,BD相交于点 , , ,以AB为直径作一个半圆,则图中阴影部分的面积为. 25. 如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .
25. 如图,在矩形ABCD中,AB=8,AD=10,AD,AB,BC分别与⊙O相切于E,F,G三点,过D作⊙O的切线交BC于点M,切点为N,则DM的长为 .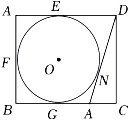 26. 建党100周年主题活动中,702班浔浔设计了如图1的“红色徽章”其设计原理是:如图2,在边长为的正方形四周分别放置四个边长为的小正方形,构造了一个大正方形 , 并画出阴影部分图形,形成了“红色徽章”的图标.现将阴影部分图形面积记作 , 每一个边长为的小正方形面积记作 , 若 , 则的值是.
26. 建党100周年主题活动中,702班浔浔设计了如图1的“红色徽章”其设计原理是:如图2,在边长为的正方形四周分别放置四个边长为的小正方形,构造了一个大正方形 , 并画出阴影部分图形,形成了“红色徽章”的图标.现将阴影部分图形面积记作 , 每一个边长为的小正方形面积记作 , 若 , 则的值是. 27. 如图,正方形ABCD的边长为4,P是边CD上的一动点,EF⊥BP交BP于G,且EF平分正方形ABCD的面积,则线段GC的最小值是.
27. 如图,正方形ABCD的边长为4,P是边CD上的一动点,EF⊥BP交BP于G,且EF平分正方形ABCD的面积,则线段GC的最小值是.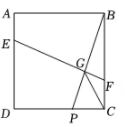 28. 正方形ABCD的边长为4,点E是BC边上的一动点,连结AE,过点B作BF⊥AE于点F,以BF为边作正方形FBHG,当点E从B运动到C时,求CF的最短距离为;线段HG扫过的面积为
28. 正方形ABCD的边长为4,点E是BC边上的一动点,连结AE,过点B作BF⊥AE于点F,以BF为边作正方形FBHG,当点E从B运动到C时,求CF的最短距离为;线段HG扫过的面积为 29. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移长度a(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的长为 .
29. 如图,在矩形ABCD中,AB=4,BC=3,将△BCD沿射线BD平移长度a(a>0)得到△B'C'D',连接AB',AD',则当△AB'D'是直角三角形时,a的长为 . 30. 如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .
30. 如图,矩形ABCD中,AB=20,AD=15,P,Q分别是AB,AD边上的动点,PQ=16,以PQ为直径的⊙O与BD交于点M,N,则MN的最大值为 .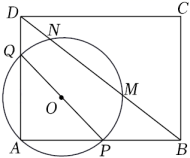
三、计算题
-
31. 如图,在中, , D为的中点, , , 连接交于点O.
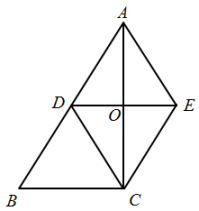 (1)、证明:四边形为菱形;(2)、若 , , 求菱形的高.32. 如图,已知在矩形ABCD中,AB=6,BC=2,点E,F分别在边CD,AB上,且DE=BF.
(1)、证明:四边形为菱形;(2)、若 , , 求菱形的高.32. 如图,已知在矩形ABCD中,AB=6,BC=2,点E,F分别在边CD,AB上,且DE=BF.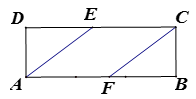 (1)、求证:四边形AFCE是平行四边形;(2)、若▱AFCE是菱形,求菱形AFCE的边长.
(1)、求证:四边形AFCE是平行四边形;(2)、若▱AFCE是菱形,求菱形AFCE的边长.四、解答题
-
33. 如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,AD=BC,求证:四边形EFGH是菱形.
 34. 如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′,此时点B′恰好落在边AD上.连接B′B,若∠AB′B=75°,求旋转角及AB长.
34. 如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A′B′C′D′,此时点B′恰好落在边AD上.连接B′B,若∠AB′B=75°,求旋转角及AB长. 35. 如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.
35. 如图,△ABC中,点D是边AC的中点,过D作直线PQ∥BC,∠BCA的平分线交直线PQ于点E,点G是△ABC的边BC延长线上的点,∠ACG的平分线交直线PQ于点F.求证:四边形AECF是矩形.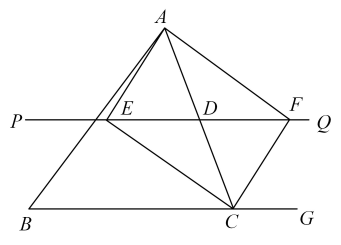 36. 在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的.
36. 在几何探究问题中,经常需要通过作辅助线(如,连接两点,过某点作垂线,作延长线,作平行线等等)把分散的条件相对集中,以达到解决问题的目的. (1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):
(1)、(探究发现)如图1,点E,F分别在正方形ABCD的边BC,CD上, ,连接EF.通过探究,可发现BE,EF,DF之间的数量关系为(直接写出结果).(2)、(验证猜想)同学们讨论得出下列三种证明思路(如图1):思路一:过点A作 ,交CD的延长线于点G.
思路二:过点A作 ,并截取 ,连接DG.
思路三:延长CD至点G,使 ,连接AG.
请选择你喜欢的一种思路证明(探究发现)中的结论.
(3)、(迁移应用)如图2,点E,F分别在正方形ABCD的边BC,CD上,且 , ,设 ,试用含 的代数式表示DF的长.37. 在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D , E , C分别在OA , AB , OB上,OD=2.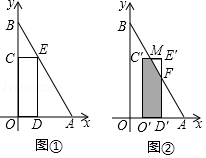
(Ⅰ)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C , O , D , E的对应点分别为C′,O′,D′,E′.设OO′=t , 矩形C′O′D′E′与△ABO重叠部分的面积为S .
①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M , F , 试用含有t的式子表示S , 并直接写出t的取值范围;
②当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
38. 阅读下面的例题及点拨,并解决问题:例题:如图①,在等边 中, 是 边上一点(不含端点 ), 是 的外角 的平分线上一点,且 .求证: .
点拨:如图②,作 , 与 的延长线相交于点 ,得等边 ,连接 .易证: ,可得 ;又 ,则 ,可得 ;由 ,进一步可得 又因为 ,所以 ,即: .
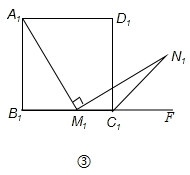
问题:如图③,在正方形 中, 是 边上一点(不含端点 ), 是正方形 的外角 的平分线上一点,且 .求证: .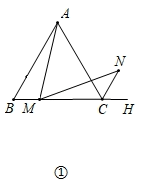

五、综合题
-
39. 将 绕点A按逆时针方向旋转 度,并使各边长变为原来的n倍,得 ,如图①,我们将这种变换记为 .
 (1)、如图①,对 作变换 得 ,则 ;直线 与直线 所夹的锐角为度;(2)、如图②, 中, ,对 作变换 得 ,使点B、C、 在同一直线上,且四边形 为矩形,求 和n的值;(3)、如图③, 中, ,对 作变换 得 ,使点B、C、 在同一直线上,且四边形 为平行四边形,求 和n的值.40. 如图
(1)、如图①,对 作变换 得 ,则 ;直线 与直线 所夹的锐角为度;(2)、如图②, 中, ,对 作变换 得 ,使点B、C、 在同一直线上,且四边形 为矩形,求 和n的值;(3)、如图③, 中, ,对 作变换 得 ,使点B、C、 在同一直线上,且四边形 为平行四边形,求 和n的值.40. 如图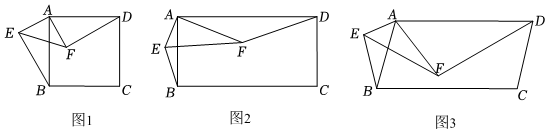 (1)、如图1,正方形ABCD与调研直角△AEF有公共顶点A,∠EAF=90°,连接BE、DF,将△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的角为β,则=;β=;(2)、如图2,矩形ABCD与Rt△AEF有公共顶点A,∠EAF=90°,且AD=2AB,AF=2AE,连接BE、DF,将Rt△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的角为β,请求出的值及β的度数,并结合图2进行说明;(3)、若平行四边形ABCD与△AEF有公共顶点A,且∠BAD=∠EAF=α(0°<α<180°),AD=kAB, AF=kAE(k≠0),将△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的锐角的度数为β,则:
(1)、如图1,正方形ABCD与调研直角△AEF有公共顶点A,∠EAF=90°,连接BE、DF,将△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的角为β,则=;β=;(2)、如图2,矩形ABCD与Rt△AEF有公共顶点A,∠EAF=90°,且AD=2AB,AF=2AE,连接BE、DF,将Rt△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的角为β,请求出的值及β的度数,并结合图2进行说明;(3)、若平行四边形ABCD与△AEF有公共顶点A,且∠BAD=∠EAF=α(0°<α<180°),AD=kAB, AF=kAE(k≠0),将△AEF绕点A旋转,在旋转过程中,直线BE、DF相交所成的锐角的度数为β,则:①=;
②请直接写出α和β之间的关系式 .