2022年中考数学二轮专题复习-平行四边形性质及判断
试卷更新日期:2022-04-09 类型:二轮复习
一、单选题
-
1. 已知在▱ABCD中,∠B+∠D=200°,则∠B的度数为( )A、100° B、160° C、80° D、60°2. 如图,在 中, , , , 则 的周长是( )
 A、16 B、20 C、21 D、233. 下列不能判定四边形ABCD是平行四边形的条件是( )A、AB∥CD,AD∥BC B、OA=OC,OB=OD C、AB∥CD,AD=BC D、AB=CD,AD=BC4. 如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A、16 B、20 C、21 D、233. 下列不能判定四边形ABCD是平行四边形的条件是( )A、AB∥CD,AD∥BC B、OA=OC,OB=OD C、AB∥CD,AD=BC D、AB=CD,AD=BC4. 如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )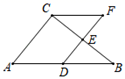 A、∠B=∠F B、∠B=∠BCF C、AC=CF D、AD=CF5. 已知△ABC(如图1),按图2、图3所示的尺规作图痕迹,不需借助三角形全等,就能推出四边形ABCD是平行四边形的依据是( )
A、∠B=∠F B、∠B=∠BCF C、AC=CF D、AD=CF5. 已知△ABC(如图1),按图2、图3所示的尺规作图痕迹,不需借助三角形全等,就能推出四边形ABCD是平行四边形的依据是( )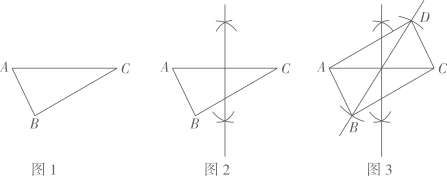 A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形6. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BD交于点F,则S∆DEF:S∆ADF:S∆ABF等于( )
A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形6. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BD交于点F,则S∆DEF:S∆ADF:S∆ABF等于( ) A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:257. 如图,四边形ABCD是一张平行四边形纸片,其高AG=2cm,底边BC=6cm,∠B=45°,沿虚线EF将纸片剪成两个全等的梯形,若∠BEF=30°,则AF的长为( )
A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:257. 如图,四边形ABCD是一张平行四边形纸片,其高AG=2cm,底边BC=6cm,∠B=45°,沿虚线EF将纸片剪成两个全等的梯形,若∠BEF=30°,则AF的长为( )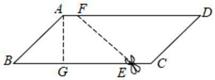 A、1cm B、 cm C、(2 ﹣3)cm D、(2﹣ )cm8.
A、1cm B、 cm C、(2 ﹣3)cm D、(2﹣ )cm8.
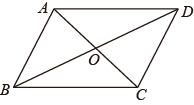
如图,平行四边形OABC的顶点O(0,0),A(1,2),点C在x轴的正半轴上,延长BA交y轴于点D.将△ODA绕点O顺时针旋转得到△OD'A',当点D的对应点D'落在OA上时,D'A'的延长线恰好经过点C,则点B的坐标为( ) A、(2 , 2) B、(2 , 2) C、(2 1,2) D、(2 1,2)9. 在面积为60的 中,过点 作 直线BC于点 ,作 直线CD于点 ,若 , ,则 的值为( )A、 B、 C、 或 D、 或10. 如图,在▱ABCD中,E、F是对角线AC上的两点,且AE=CF,有下列结论:①BE=DF,②BE∥DF,③AB=DE;④四边形EBFD为平行四边形;⑤ ;⑥ .其中正确结论的是( )
A、(2 , 2) B、(2 , 2) C、(2 1,2) D、(2 1,2)9. 在面积为60的 中,过点 作 直线BC于点 ,作 直线CD于点 ,若 , ,则 的值为( )A、 B、 C、 或 D、 或10. 如图,在▱ABCD中,E、F是对角线AC上的两点,且AE=CF,有下列结论:①BE=DF,②BE∥DF,③AB=DE;④四边形EBFD为平行四边形;⑤ ;⑥ .其中正确结论的是( ) A、3 B、4 C、5 D、611. 如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( )
A、3 B、4 C、5 D、611. 如图,已知平行四边形ABCD的面积为100,P为边CD上的任意一点,E,F分别是线段PA,PB的中点,则图中阴影部分的总面积为( ) A、30 B、25 C、22.5 D、5012. 如图,E是▱ABCD的边AD上的点,且= , 连接BE并延长,交CD的延长线于点F,若DE=DF=3,则▱ABCD的周长为( )
A、30 B、25 C、22.5 D、5012. 如图,E是▱ABCD的边AD上的点,且= , 连接BE并延长,交CD的延长线于点F,若DE=DF=3,则▱ABCD的周长为( ) A、15 B、24 C、30 D、3613. 如图,在▱ABCD中,对角线AC,BD相交于点O,将△AOB平移至△DPC的位置,连结OP,则图中平行四边形的个数为( )
A、15 B、24 C、30 D、3613. 如图,在▱ABCD中,对角线AC,BD相交于点O,将△AOB平移至△DPC的位置,连结OP,则图中平行四边形的个数为( ) A、1 B、2 C、3 D、414. 如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的有( )
A、1 B、2 C、3 D、414. 如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的有( )
①图甲,DE⊥AC,BF⊥AC;②图乙,DE平分∠ADC,BF平分∠ABC;③图丙,E是AB的中点,F是CD的中点;④图丁,E是AB上一点,EF⊥AB。
A、3个 B、4个 C、1个 D、2个15. 如图,在平行四边形ABCD中,过对角线BD上一点P,作EF∥BC,HG∥AB,若四边形AEPH和四边形CFPG的面积分另为S1和S2 , 则S1与S2的大小关系为( ) A、S1=S2 B、S1>S2 C、S1<S2 D、不能确定16. 如图,在平面直角坐标系中,平行四边形 的边 在y轴的正半轴上,反比例函数 的图象分别交 于中点D,交 于点E,且 ,连接 ,若 ,则k的值为( )
A、S1=S2 B、S1>S2 C、S1<S2 D、不能确定16. 如图,在平面直角坐标系中,平行四边形 的边 在y轴的正半轴上,反比例函数 的图象分别交 于中点D,交 于点E,且 ,连接 ,若 ,则k的值为( ) A、5 B、 C、6 D、17. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、18. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( )
A、5 B、 C、6 D、17. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、18. 如图,在 中, , , .分别以点B、D为圆心,大于 长为半径画弧,两弧相交于点M、N,直线MN分别与AD、BC相交于点E、F,则EF的长为( ) A、 B、4 C、 D、19. 如图,在平行四边形ABCD中,AB⊥BD,sinA= ,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= (k>0)同时经过B、D两点,则k的值为( )
A、 B、4 C、 D、19. 如图,在平行四边形ABCD中,AB⊥BD,sinA= ,将平行四边形ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y= (k>0)同时经过B、D两点,则k的值为( )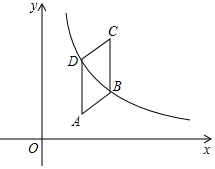 A、 B、 C、 D、20. 如图, 中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且 交AB于E , 且 交AD于F , 则阴影部分的面积为( )
A、 B、 C、 D、20. 如图, 中, , , ,P是对角线AC上任一点(点P不与点A、C重合),且 交AB于E , 且 交AD于F , 则阴影部分的面积为( ) A、5 B、 C、10 D、
A、5 B、 C、10 D、二、填空题
-
21. 如图,学校大门口的电动伸缩门,其中间部分都是四边形的结构,这是应用了四边形的 .
 22. 在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .23. 已知O、A、B的坐标分别是 , 在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为.24. 如图,在 中,E是AD边上一点,AE:ED=1:2,连结AC,BE交于点F.若 ,则 = .
22. 在平行四边形ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC的长为 .23. 已知O、A、B的坐标分别是 , 在平面内找一点M,使得以点O、A、B、M为顶点的四边形是平行四边形,则点M的坐标为.24. 如图,在 中,E是AD边上一点,AE:ED=1:2,连结AC,BE交于点F.若 ,则 = . 25. 如图, ▱ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连结BE,若 □ ABCD的周长为28,则△ABE的周长为.
25. 如图, ▱ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连结BE,若 □ ABCD的周长为28,则△ABE的周长为. 26. 如图,AB是半圆O的弦,DE是直径,过点B的切线BC与⊙O相切于点B,与DE的延长线交于点C,连接BD,若四边形OABC为平行四边形,则∠BDC的度数为.
26. 如图,AB是半圆O的弦,DE是直径,过点B的切线BC与⊙O相切于点B,与DE的延长线交于点C,连接BD,若四边形OABC为平行四边形,则∠BDC的度数为. 27. 如图,已知▱ABCD的面积为56,AC与BD相交于O点,则图中阴影部分的面积是。
27. 如图,已知▱ABCD的面积为56,AC与BD相交于O点,则图中阴影部分的面积是。 28. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.
28. 如图所示,在 中, 是AD边的中点, 是AB边上的一动点,将 沿MN所在直线翻折得到 ,连结 ,则 长度的最小值是.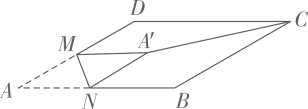 29. 在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为.
29. 在平行四边形 中, , ,将 沿对角线 翻折至 ,连接 .若 ,则点C到 边的距离为.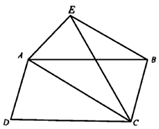 30. 如图,点 , 分别是矩形 的边 , 的中点,两条平行线 , 分别经过菱形 的顶点 , 和边 , 的中点 , ,已知菱形 的面积为 ,则图中阴影部分的面积和为 (用含 的代数式表示)
30. 如图,点 , 分别是矩形 的边 , 的中点,两条平行线 , 分别经过菱形 的顶点 , 和边 , 的中点 , ,已知菱形 的面积为 ,则图中阴影部分的面积和为 (用含 的代数式表示)
三、计算题
-
31. 如图,四边形 是平行四边形, 且分别交对角线 于点E , F .
 (1)、求证: ;(2)、当四边形 分别是矩形和菱形时,请分别说出四边形 的形状.(无需说明理由)32. 如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD , CD∥AB . 若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
(1)、求证: ;(2)、当四边形 分别是矩形和菱形时,请分别说出四边形 的形状.(无需说明理由)32. 如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD , CD∥AB . 若⊙O的半径为1,求图中阴影部分的面积(结果保留π).
四、解答题
-
33. 已知;如图,在 中, ,点 是 的中点,若 , .
求证:
 34. 如图所示,在ABCD中,分别以AB,CD为边向外作等边△ABE和等边△CDF,连结BD,EF。求证:EF与BD互相平分。
34. 如图所示,在ABCD中,分别以AB,CD为边向外作等边△ABE和等边△CDF,连结BD,EF。求证:EF与BD互相平分。 35. 如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。
35. 如图,在▱ABCD中,对角线AC⊥BC,∠BAC=30°,BC=2 ,在AB边的下方作射线AG,使得∠BAG=30°,E为线段DC上一个动点,在射线AG上取一点P,连接BP,使得∠EBP=60°,连接EP交AC于点F,在点E的运动过程中,当∠BPE=60°时,求 AF长。 36. (感知)如图①,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交边AD、BC于点E、F,易证:OE=OF(不需要证明);
36. (感知)如图①,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交边AD、BC于点E、F,易证:OE=OF(不需要证明);(探究)如图②,平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交边BA、DC的延长线于E、F,求证:OE=OF;
(应用)连结图②中的DE、BF,其它条件不变,如图③,若AB=2AE,△AOE的面积为1,则四边形BEDF的面积为.

五、综合题
-
37. 如图,在△ABC中,点D,E分别是边AB,BC的中点,点F,G是边AC的三等分点,DF,EG的延长线相交于点H.

求证:
(1)、DF//BG,DF= BG;(2)、四边形FBGH是平行四边形;(3)、四边形ABCH是平行四边形.38. 如图
 (1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。
(1)、如图1,在▱ABCD中,AE平分∠BAD交CD边于点E,已知AB=5cm,AD=3cm,则EC等于cm。(2)、如图2,在▱ABCD中,若AE,BE分别是∠DAB,∠CBA的平分线,点E在DC边上,且AB=4,则ABCD的周长为。(3)、如图3,已知四边形ABCD是平行四边形,AD=BC,若AF,BE分别是∠DAB,∠CBA的平分线。求证:DF=EC(4)、在(3)的条件下,如果AD=3,AB=5,则EF的长为。