2022年北师大数学七下期末复习阶梯训练: 概率初步(优生集训)
试卷更新日期:2022-04-08 类型:复习试卷
一、综合题
-
1. 掷一枚质地均匀的骰子,观察向上一面的点数,求下列事件的概率.
 (1)、点数为2.(2)、点数为奇数.(3)、点数大于1且小于6.2. 在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.(1)、求从布袋中摸出一个球是红球的概率;(2)、现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是 ,问取走了多少个白球?3. 在一个不透明的袋子中装有除颜色外都相同的黄球、绿球和红球共12个,其中红球有2个.(1)、摸到红球的概率是;(2)、若摸到绿球的概率是 ,求袋子中黄球的个数.4. 如图所示,是一个均匀的可以自由转动的转盘;某购物广场举办有奖销售活动,顾客每购物满100元,就获得一-次转这个转 盘的机会.请你根据以上信息:
(1)、点数为2.(2)、点数为奇数.(3)、点数大于1且小于6.2. 在一个不透明的布袋中装有8个红球和16个白球,它们除颜色不同外其余都相同.(1)、求从布袋中摸出一个球是红球的概率;(2)、现从布袋中取走若干个白球,并放入相同数目的红球,搅拌均匀后,再从布袋中摸出一个球是红球的概率是 ,问取走了多少个白球?3. 在一个不透明的袋子中装有除颜色外都相同的黄球、绿球和红球共12个,其中红球有2个.(1)、摸到红球的概率是;(2)、若摸到绿球的概率是 ,求袋子中黄球的个数.4. 如图所示,是一个均匀的可以自由转动的转盘;某购物广场举办有奖销售活动,顾客每购物满100元,就获得一-次转这个转 盘的机会.请你根据以上信息: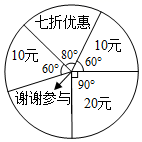 (1)、求:顾客转出“七折优惠”的概率;(2)、求:顾客转出“得20元”的概率;(3)、求:顾客中奖的概率.5. 一只不透明的箱子里共有8个球,其中2个白球,1个红球,5个黄球,它们除颜色外均相同.(1)、从箱子中随机摸出一个球是白球的概率是多少?(2)、再往箱子中放入多少个黄球,可以使摸到白球的概率变为0.2?6. 在一个口袋中只装有4个白球和11个红球,它们除颜色外完全相同.(1)、事件“从口袋中随机摸出一个球是绿球”发生的概率是;(2)、事件“从口袋中随机摸出一个球是白球”发生的概率是;(3)、在袋中15球保持不变的情况下,摸到红球的概率为 ,则口袋中红球、白球各多少个?7. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.(1)、先从袋子中取出 个红球( 且 为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.
(1)、求:顾客转出“七折优惠”的概率;(2)、求:顾客转出“得20元”的概率;(3)、求:顾客中奖的概率.5. 一只不透明的箱子里共有8个球,其中2个白球,1个红球,5个黄球,它们除颜色外均相同.(1)、从箱子中随机摸出一个球是白球的概率是多少?(2)、再往箱子中放入多少个黄球,可以使摸到白球的概率变为0.2?6. 在一个口袋中只装有4个白球和11个红球,它们除颜色外完全相同.(1)、事件“从口袋中随机摸出一个球是绿球”发生的概率是;(2)、事件“从口袋中随机摸出一个球是白球”发生的概率是;(3)、在袋中15球保持不变的情况下,摸到红球的概率为 ,则口袋中红球、白球各多少个?7. 在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黄球6个.(1)、先从袋子中取出 个红球( 且 为正整数),再从袋子中随机摸一个小球,将“摸出黄球”记为事件A.①若事件 为必然事件,则 的值为;
②若事件 为随机事件,则 的值为 .
(2)、先从袋子中取出 个红球,再放入 个一样的黄球并摇匀,经过多次试验,随机摸出一个黄球的频率在 附近摆动,求 的值.8. 某校为了了解初中学生一周内的课外阅读的时间(单位为h),随机调查了该校的部分初中学生,根据调查结果,绘制出如图的统计图.请根据相关信息,解答下列问题: (1)、扇形统计图中的m= , 条形统计图中的n=(2)、从该样本中随机抽取一名学生一周内的课外阅读的时长,恰好是7h的概率是多少?9. 如图,现有一个转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求:
(1)、扇形统计图中的m= , 条形统计图中的n=(2)、从该样本中随机抽取一名学生一周内的课外阅读的时长,恰好是7h的概率是多少?9. 如图,现有一个转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求: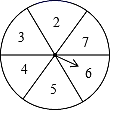 (1)、转到数字10是(从“不确定事件”“必然事件”“不可能事件”选一个填入);(2)、转动转盘,转出的数字大于3的概率是;(3)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
(1)、转到数字10是(从“不确定事件”“必然事件”“不可能事件”选一个填入);(2)、转动转盘,转出的数字大于3的概率是;(3)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
10. 如图是小彬设计的一个圆形转盘转盘被均匀的分成8份,分别标有1、2、3、4、5、6、7、8这8个数,转动转盘,当转盘停止时,指针指向的数即为转出的数.(当指针恰好指在分界线上时,无效重转)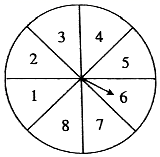 (1)、求小彬转出的数是3的倍数的概率.(2)、现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?11. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏;小明从中任意抽取一张牌(不放回) ,小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.(1)、若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?12. 某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:(1)、该班小明同学恰好抽到丙类名额的概率是;(2)、该班小丽同学能有幸去参加游学活动的概率是;(3)、后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?13. 有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题:
(1)、求小彬转出的数是3的倍数的概率.(2)、现有两张分别写有3和5的卡片,随机转动转盘,转盘停止后记下转出的数,与两张卡片上的数分别作为三条线段的长度.这三条线段能构成三角形的概率是多少?11. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏;小明从中任意抽取一张牌(不放回) ,小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.(1)、若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?12. 某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:(1)、该班小明同学恰好抽到丙类名额的概率是;(2)、该班小丽同学能有幸去参加游学活动的概率是;(3)、后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?13. 有一个转盘(如图所示),被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;③指针指向黄色;④指针不指向黄色.估计各事件的可能性大小,完成下列问题: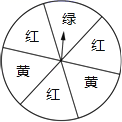 (1)、可能性最大和最小的事件分别是哪个?(2)、将这些事件的序号按发生的可能性从小到大的顺序排列:.14. 一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少2个,从袋中摸出一个球是黄球的概率为0.4.(1)、求袋中红、黄、白三种颜色的球的个数;(2)、向袋中放入若干个红球,使摸出一个球是红球的概率为0.7,求放入红球的个数;(3)、在(2)的条件下,求摸出一个球是白球的概率.15. 如图所示有 张质地大小完全相同的卡片,分别写有 这九个数字,将它们背面朝上洗匀后,任意抽出一张.
(1)、可能性最大和最小的事件分别是哪个?(2)、将这些事件的序号按发生的可能性从小到大的顺序排列:.14. 一个不透明的袋中装有红、黄、白三种颜色的球共10个,它们除了颜色外完全相同,其中黄球个数比白球个数的3倍少2个,从袋中摸出一个球是黄球的概率为0.4.(1)、求袋中红、黄、白三种颜色的球的个数;(2)、向袋中放入若干个红球,使摸出一个球是红球的概率为0.7,求放入红球的个数;(3)、在(2)的条件下,求摸出一个球是白球的概率.15. 如图所示有 张质地大小完全相同的卡片,分别写有 这九个数字,将它们背面朝上洗匀后,任意抽出一张. (1)、抽到数字 的概率是 .(2)、抽到奇数的概率是 .(3)、抽到两位数的概率是 .16. 如图1和图2均是一个均匀的可以自由转动的转盘,图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转);图2被涂上红色与绿色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色(当指针恰好指在分界线上时重转).小明转动图1的转盘,小亮转动图2的转盘.
(1)、抽到数字 的概率是 .(2)、抽到奇数的概率是 .(3)、抽到两位数的概率是 .16. 如图1和图2均是一个均匀的可以自由转动的转盘,图1被平均分成9等份,分别标有1,2,3,4,5,6,7,8,9这9个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字(当指针恰好指在分界线上时重转);图2被涂上红色与绿色,转动转盘,当转盘停止后,指针指向的颜色即为转出的颜色(当指针恰好指在分界线上时重转).小明转动图1的转盘,小亮转动图2的转盘.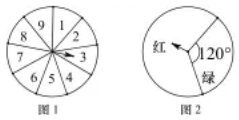 (1)、求小明转出的数字小于7的概率.(2)、小穎认为,小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同,她的看法对吗?为什么?17. 已知一个纸箱中装有除颜色外完全相同的红球、黄球、黑球共80个,从中任意摸出一个球,摸到红球、黄球的概率分别为0.2和0.3.(1)、求黑球的数量;(2)、若从纸箱中取走若干个黑球,并放入相同数量的红球,要使从纸箱中任意摸出一个球是红球的概率为 , 求放入红球的数量.18. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
(1)、求小明转出的数字小于7的概率.(2)、小穎认为,小明转出来的数字小于7的概率与小亮转出的颜色是红色的概率相同,她的看法对吗?为什么?17. 已知一个纸箱中装有除颜色外完全相同的红球、黄球、黑球共80个,从中任意摸出一个球,摸到红球、黄球的概率分别为0.2和0.3.(1)、求黑球的数量;(2)、若从纸箱中取走若干个黑球,并放入相同数量的红球,要使从纸箱中任意摸出一个球是红球的概率为 , 求放入红球的数量.18. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的= ;= ;(2)、请估计:当次数s很大时,摸到白球的频率将会接近(精确到0.1);(3)、请推算:摸到红球的概率是(精确到0.1).19. 在一个不透明的口袋里装有4个白球和6个红球,它们除颜色外完全相同.(1)、事件“从口袋里随机摸出一个球是绿球”发生的概率是;(2)、事件“从口袋里随机摸出一个球是红球”发生的概率是;(3)、从口袋里取走x个红球后,再放入x个白球,并充分摇匀,若随机摸出白球的概率是 , 求x的值.20. 一个口袋中装有4个白球、6个红球,这些球除颜色外完全相同,重复搅匀后随机摸出一球,发现是白球.(1)、如果将这个白球放回,再摸出一球,那么它是白球的概率是多少?(2)、如果这个白球不放回,再摸出一球,那么它是白球的概率是多少.21. 一个口袋中放有200个涂有红、黑、黄三种颜色的质地相同的小球,若红球个数是黑球个数的2倍多30个,从袋中任取一个球是黄球的概率是 .(1)、求袋中黄球的个数;(2)、求袋中红球的个数;(3)、求从袋中任取一球是黑球的概率.22. 某商场购进一批名牌衬衫,要求一等品的数量12850件左右,请问该商场应购进多少件这样的衬衫?下面是该部门经理随机抽查一些衬衫后,统计得到的一等品的频率变化表:(1)、把表格补充完整(结果保留两位小数);抽查数n
100
200
1500
2000
2500
一等品数m
94
1430
1902
一等品频率
0.97
0.95
(2)、任意抽取1件衬衫,抽得一等品的概率约为多少?(3)、你能求得商场应购进多少件这样的衬衫吗?23. 在一个不透明的盒子里装有除颜色外完全相同的红、白、黑三种颜色的球,其中红球3个,白球5个,黑球若干个.若从中任意摸出一个白球的概率是 .(1)、求盒子中黑球的个数;(2)、求任意摸出一个球是黑球的概率;(3)、能否通过改变盒子中球的数量,使得任意摸出一个球是红球的概率为 ,若能,请写出你的修改方案.24. “五·一”期间,某书城为了招徕顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元图书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.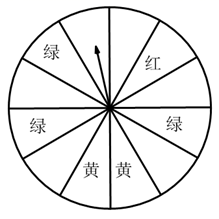 (1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.25. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?
(1)、写出任意转动一次转盘获得购书券的概率;(2)、写出任意转动一次转盘获得45元,30元,25元的概率.25. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?