2022年北师大数学七下期末复习阶梯训练： 生活中的轴对称（优生集训）
试卷更新日期：2022-04-08 类型：复习试卷
一、综合题
-
1. 生活中，有人喜欢把传送的便条折成“
”形状，折叠过程按图①、②、③、④的顺序进行（其中阴影部分表示纸条的反面）：如果由信纸折成的长方形纸条（图①）长为厘米，分别回答下列问题：
(1)、如果长方形纸条的宽为厘米，并且开始折叠时起点与点的距离为厘米，那么在图②中，厘米； 在图④中，厘米．(2)、如果长方形纸条的宽为厘米，现不但要折成图④的形状，而且为了美观，希望纸条两端超出点的长度相等，即最终图形是轴对称图形，试求在开始折叠时起点与点的距离（结果用表示）．2. 在数轴上， 已知在纸面上有一数轴 (如图)， 折叠纸面.
(1)、若1表示的点与-1表示的点重合， 则-2表示的点与何数表示的点重合；(2)、若- 1表示的点与5表示的点重合， 0表示的点与何数表示的点重合；(3)、若- 1表示的点与5表示的点之间的线段对折2次， 展开后， 请写出所有的折点表示的数?3. 如图，从数轴上的原点开始，先向左移动1cm到达A点，再向左移动4cm到达B点，然后向右移动10cm到达C点．
(1)、用1单位长度表示1cm，请你在题中所给的数轴上表示出A、B、C三点的位置；(2)、把这条数轴在数m处对折，使表示﹣11和2017两数的点恰好互相重合，则与B点重合的点所表示的数是 ， m＝ ．(3)、把点C到点A的距离记为CA，点B到点A的距离记为BA，①CA﹣BA＝ ▲ cm；
②若点B以每秒3cm的速度向左移动，同时A、C以每秒1cm、5cm的速度向右移动，设移动时间为t（t＞0）秒，试探究CA﹣AB的值是否会随着t的变化而改变？请说明理由．
4. 如图①，将一张长方形纸片沿EF对折，使AB落在 的位置；
(1)、若∠1的度数为a，试求∠2的度数（用含a的代数式表示）；(2)、如图②，再将纸片沿GH对折，使得CD落在 的位置.①若 ，∠1的度数为a，试求∠3的度数（用含a的代数式表示）：
②若 ，∠3的度数比∠1的度数大20°，试计算∠1的度数.
5. 如图，已知直线AB∥射线CD，∠CEB=110°。P是射线EB上一动点，过点P作PQ∥EC交射线CD于点Q，连接CP，作∠PCF=∠PCQ，交直线AB于点F，CG平分∠ECF。
(1)、若点P，F，G都在点E的右侧、①求∠PCC的度数；
②若EGC-∠ECG=30°，求∠CPQ的度数。（不能使用“三角形的内角和是180°”直接解题）
(2)、在点P的运动过程中，是否存在这样的情形。使∠ECC：∠EFC=3：2？若存在，直接写出∠CPQ的度数；若不存在，请说明理由。6. 问题解决：
(1)、问题情境：如图1所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到P的距离之和最短？请画出点P的位置；(2)、问题理解：如图2，在△ABC中，AB＝AC，AD平分∠BAC，点E是AC边的中点，点P是线段AD上的动点，画出PC＋PE取得最小值时点P的位置；(3)、问题运用：如图3，在△ABC中，AB＝AC＝13，BC＝10，AD＝12，AD是∠BAC的平分线，当点E、P分别是AC和AD上的动点时，求PC＋PE的最小值．7. 已知：直线a∥b ， 点A ， B在直线a上，点C ， D在直线b上，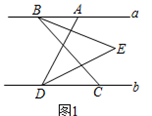
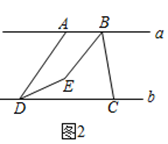
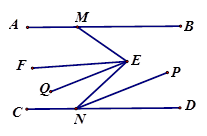图3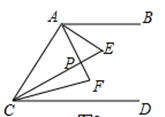
图4(1)、连接AD ， BC ， BE平分∠ABC ， DE平分∠ADC ， 且BE ， DE所在的直线交于点E ．①如图1，若∠ABC＝60°，∠ADC＝70°，则∠BED的度数为；
②如图2，设∠ABC＝α，∠ADC＝β，则∠BED的度数为（用含有α，β的式子表示）．
(2)、如图3，EF平分∠MEN ， NP平分∠END ， EQ//NP ， 则∠FEQ和∠BME的数量关系是。(3)、如图4，若∠BAP＝ ∠BAC ， ∠DCP＝ ∠ACD ， 且AE平分∠BAP ， CF平分∠DCP ， 猜想∠E+∠F的结果并且证明你的结论；8. 如图，AD BC，∠BAD的平分线交BC于点G．∠BCD＝90°．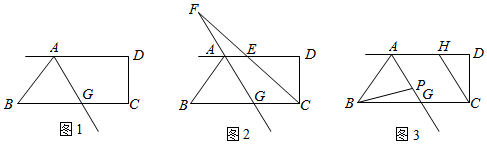
(1)、试说明：∠BAG＝∠BGA：(2)、如图2，∠BCD的平分线交AD于点E交射线GA于点F，①写出∠AFC，∠BAG的数量关系，并说明理由．
②若∠ABG＝55°，则∠AFC＝ ▲ ．
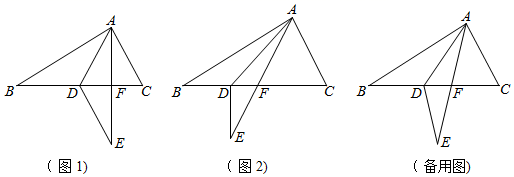
(3)、如图3，线段AG上有点P，满足∠ABP＝3∠PBG，过点C作CH∥AG．若在直线AG上取一点M，使∠PBM＝∠DCH，则 的值是 ．9. 教材呈现：如图是华师版七年级下册数学教材第76页的部分内容．如图，已知△ABC分别用∠1、∠2、∠3表示△ABC的三个内角，证明∠1+∠2+∠3＝180°．
解：延长BC至点E，以点C为顶点，在BE的上侧作∠DCE＝∠2，则CD∥BA（同位角相等，两直线平行）
(1)、请根据教材提示，结合图一，将证明过程补充完整．(2)、结论应用：①如图二，在△ABC中，∠A＝60°，BP平分∠ABC，CP平分∠ACB，求∠BPC的度数．
②如图三，将△ABC的∠A折叠，使点A落在△ABC外的A1处，折痕为DE．若∠A＝α，∠BDA1＝β，∠CEA1＝γ，则α、β、γ满足的等量关系为 ▲ （用含α、β、γ的代数式表示）．
10. 如图，在等边 中，已知点 在直线 上（不与点 、 重合），点 在直线 上，且 ．
图1
图2
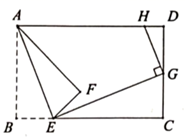
(1)、若点 为线段 的中点时，求证： ；(2)、若 的边长为2， ．求 的长．11. 已知长方形纸片ABCD ， 点E在边AB上，点F、G在边CD上，连接EF、EG ． 将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN ．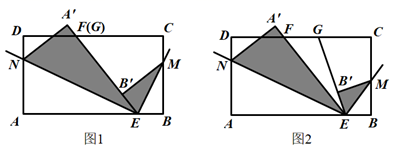
(1)、如图1，若点F与点G重合，求∠MEN的度数；(2)、如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；(3)、若∠MEN＝α，请直接用含α的式子表示∠FEG的大小．12. 如图1，将一段长为60cm绳子AB拉直铺平后折叠（绳子无弹性，折叠处长度忽略不计），使绳子与自身一部分重叠.
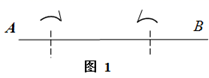(1)、若将绳子AB沿M、N点折叠，点A、B分别落在 、 处.①如图2，若 、 恰好重合于点О处，MN= cm；
②如图3，若点 落在点 的左侧，且 ，MN= cm；
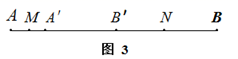
③若 ，MN= cm.（用含n的代数式表示）
(2)、如图4，若将绳子AB沿N点折叠后，点B落在 处，在重合部分 上沿绳子垂直方向剪断，将绳子分为三段，若这三段的长度由短到长的比为3：4：5，直接写出AN所有可能的长度.
13. 已知长方形纸片ABCD，点E在边AB上，点F、G在边CD上，连接EF、EG，将∠BEG对折，点B落在直线EG上的点B′处，得折痕EM；将∠AEF对折，点A落在直线EF上的点A′处，得折痕EN．(1)、如图1，若点F与点G重合，求∠MEN的度数；
(2)、如图2，若点G在点F的右侧，且∠FEG＝30°，求∠MEN的度数；
14. 利用折纸可以作出角平分线．
(1)、如图1，若∠AOB＝58°，则∠BOC＝ ．(2)、折叠长方形纸片，OC，OD均是折痕，折叠后，点A落在点A′，点B落在点B'，连接OA'．①如图2，当点B'在OA'上时，判断∠AOC与∠BOD的关系，并说明理由；
②如图3，当点B'在∠COA'的内部时，连接OB'，若∠AOC＝44°，∠BOD＝61°，求∠A'OB'的度数．
15. 如图， 与 的角平分线交于点P．
(1)、若 ， ，求 的度数；(2)、猜想 ， ， 的等量关系．16. 阅读思考：小迪在学习过程中，发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示，探索过程如下：如图1所示，线段 的长度可表示为： ， 于是他归纳出这样的结论：如果点A表示的数为a，点B表示的数为b，当 时， （较大数一较小数）.
(1)、尝试应用：①如图2所示，计算： ， ；
②把一条数轴在数m对应的点处对折，使表示-20和2020两数的点恰好互相重合，求数m的值；
(2)、问题解决：①如图3所示，点P表示数x，点M表示数 ， 点N表示数 ， 且 ， 求出点P和点N分别表示的数；
②在上述①的条件下，是否存在点Q，使 ？若存在，请直接写出点Q所表示的数；若不存在，请说明理由.
17. 阅读思考：小芬在学习过程中，发现“数轴上两点间的距离”可以用“表示这两点数的差”来表示，探索过程如下：如图1所示，线段AB，BC，CD的长度可表示为：AB＝3＝4﹣1，BC＝5＝4﹣（﹣1），CD＝3＝（﹣1）﹣（﹣4），于是他归纳出这样的结论：如果点A表示的数为a，点B表示的数为b，当b＞a时，AB＝b﹣a（较大数﹣较小数）.
(1)、尝试应用：①如图2所示，计算：OE＝ ， EF＝；
②把一条数轴在数m处对折，使表示﹣18和2020两数的点恰好互相重合，则m＝；
(2)、问题解决：①如图3所示，点P表示数x，点M表示数﹣2，点N表示数2x+14，且MN＝4PM，求出点P和点N分别表示的数；
②在上述①的条件下，是否存在点Q，使PQ+QN＝3QM？若存在，请直接写出点Q所表示的数；若不存在，请说明理由.
18. 同学们，我们己学习了角平分线的概念和性质，那么你会用它们解决有关问题吗？
(1)、如图（1），已知 ，请你画出它的角平分线 ， 并填空：因为OC是 的平分线，所以∠ =∠(2)、如图（2），已知 ，若将 沿着射线OC翻折，射线OA落在OB处，请你画出射线OB，射线OC一定平分 ．理由如下：因为 是由 翻折而成，而翻折不改变图形的形状和大小，所以 ， 所以射线 是∠的角平分线．
(3)、拓展应用
如图（3），将长方形纸片的一角折叠，使顶点A落在C处，折痕为 ，再将它的另一个角也折叠，顶点B落在OC上的D处并且使OD过点C，折痕为OF．直接利用（2）的结论；①若 ，求 的度数．（写出计算说理过程）
②若 ，求 的度数，从计算中你发现了 的度数有什么规律？（写出计算说理过程）
19. 如图1，点O为直线AB上一点，过点O作射线OC ， 使∠BOC＝50°.现将一直角三角板的直角顶点放在点O处，一边OD与射线OB重合，如图2.
(1)、∠EOC＝；(2)、如图3，将三角板DOE绕点O逆时针旋转一定角度，此时OC是∠EOB的角平分线，求∠BOD的度数；(3)、将三角板DOE绕点O逆时针旋转，在OE与OA重合前，是否有某个时刻满足∠DOC＝ ∠AOE ， 求此时∠BOD的度数.20. 如图
(1)、如图1，射线OC在 的内部，OM平分 ，ON平分 ，若 ，求 的度数；(2)、射线OC ， OD在 的内部，OM平分 ，ON平分 ，若 ， ，求 的度数；(3)、在（2）中， ， ，其他条件不变，请用含m ， n的代数式表示MON的度数 不用说理 ．21. 将一副三角板如图1摆放， ， ， 平分 ， 平分 .
(1)、 =；(2)、将图1中的三角板 绕点 旋转到图2的位置，求 ；(3)、将图1中的三角板 绕点 旋转到图3的位置，求 .22. 如图，已知数轴上两点A、B对应的数分别为﹣1、3，点P为数轴上一动点，其对应的数为x.
(1)、若点P到点A、点B的距离相等，求点P对应的数是；(2)、数轴上存在点P到点A、点B的距离之和为10，则x＝；(3)、若将数轴折叠，使﹣1与3表示的点重合，则﹣3表示的点与数表示的点重合；(4)、若数轴上M、N两点之间的距离为2021（M在N的左侧），且M、N两点经过（3）折叠后互相重合，则M，N两点表示的数分别是：M： ， N：.23. 操作探究：已知在纸面上有一数轴左右对折纸面，折痕所在的直线与数轴的交点为“对折中心点”．(1)、操作一：左右对折纸面，使1对应的点与-1对应的点重合，则-3对应的点与对应的点重合；(2)、操作二：左右对折纸面，使-1对应的点与3对应的点重合，回答以下问题：①对折中心点对应的数为 ， 对折后5对应的点与数对应的点重合；
②若数轴上A、B两点之间的距离为11（A在B的左侧），且A、B两点经折叠后重合，通过计算求A、B两点对应的数分别是多少？
(3)、操作三：已知数轴上的点A对应的数是a，点B对应的数是b，对折中心点C对应的数是c，此时点A与点B对折重合，那么a，b，c三数满足的关系式为 ．
24. 如图①，在数轴上有一条线段AB，点A，B表示的数分别是﹣2和﹣11.
(1)、若M是线段AB的中点，则点M在数轴上对应的数为.(2)、若C为线段AB上一点，如图②，以点C为折点，将此数轴向右对折；如图③，点B落在点A的右边点B′处，若AB′＝ B′C，求点C在数轴上对应的数是多少？
