2022年北师大数学七下期末复习阶梯训练： 生活中的轴对称（优生加练）
试卷更新日期：2022-04-08 类型：复习试卷
一、单选题
-
1. 如图，在△ABC中，∠ABC=50°，∠ACB=100°，点M是射线AB上的一个动点，过点M作MN∥BC交射线AC于点N，连结BN。若△BMN中有两个角相等，则∠MNB的度数不可能是（ ）
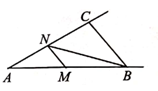A、25° B、30° C、50° D、65°2. 小明受“求2×2方格中阴影正方形边长（如图1）”启发，将宽AB为1的长方形纸片（如图2）沿着AE折叠，使得AB落在AD边上，点B和点F重合，再将折好的纸片沿着AH折叠，使得AE落在AD上，刚好点E和点D重合，则DF的长为（ ）
A、 B、 C、1 D、3. 如图，直角梯形纸片对边 ， 是直角，将纸片沿着EF折叠，DF的对应边 交AB于点G，FH平分 交AC于点H.则结论：① ；② ；③ ；④若 ，则 .其中正确结论的个数为（ ）
A、4个 B、3个 C、2个 D、1个4. 如图，将一张长方形纸片 沿着 折叠，使点 分别落在 处．若 ，则 的度数为（ ）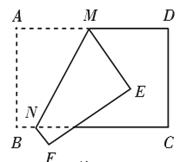
A、 B、 C、 D、5. 如图，在第1个△A1BC中，∠B＝30°，A1B＝CB；在边A1B上任取一点D，延长CA1到A2 ， 使A1A2＝A1D，得到第2个△A1A2D；在边A2D上任取一点E，延长A1A2到A3 ， 使A2A3＝A2E，得到第3个△A2A3E，…按此做法继续下去，则第n个三角形中以An为顶点的底角度数是（ ）
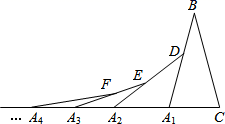A、（ ）n•75° B、（ ）n﹣1•65° C、（ ）n﹣1•75° D、（ ）n•85°6. 如图，线段AB，DE的垂直平分线交于点C，且∠ABC=∠EDC=62°，∠AEB=82°，则∠EBD的度数为（ ）
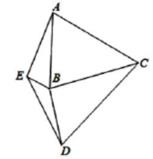A、108° B、118° C、138° D、144°7. 如图，将一条两边沿互相平行的纸带折叠，已知 ，则∠1=（ ）
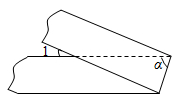A、28° B、30° C、38° D、45°8. 如图1，在矩形纸片ABCD中，AB＝83，AD＝10，点E是CD的中点．将这张纸片依次折叠两次：第一次折叠纸片使点A与点E重合，如图2，折痕为MN，连接ME、NE；第二次折叠纸片使点N与点E重合，如图3，点B落在 处，折痕为HG，连接HE．①∠DME＝2∠ANM；②MH＝HN；③∠AMN＝∠GHN；④ GE≌ BGN，以上说法正确的有（ ）个．
A、1个 B、2个 C、3个 D、4个9. 如图，把△ABC纸片沿DE折叠，当A落在四边形BCDE内时，则 ∠A 与 ∠1+∠2 之间有始终不变的关系是（ ）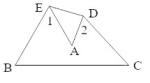
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=∠1+∠2 D、3∠A=2（∠1+∠2）10. 若数轴上A，B两点之间的距离为8个单位长度，点A表示的有理数是﹣10，并且A，B两点经折叠后重合，此时折线与数轴的交点表示的有理数是（ ）
A、﹣6 B、﹣9 C、﹣6或﹣14 D、﹣1或﹣9二、填空题
-
11. 如图1，在一条可以折叠的数轴上有点A，B，C，其中点A，点B表示的数分别为﹣16和9，现以点C为折点，将数轴向右对折，点A对应的点A1落在B的右边；如图2，再以点B为折点，将数轴向左折叠，点A1对应的点A2落在B的左边.若A2、B之间的距离为3，则点C表示的数为.
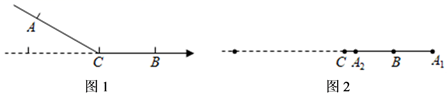12. 根据下面给出的数轴，解答下面的问题：
(1)、请你根据图中A、B两点的位置，分别写出它们所表示的有理数A： ， B：；
(2)、观察数轴，与点A的距离为4的点表示的数是：；(3)、若将数轴折叠，使得A点与﹣3表示的点重合，则B点与数表示的点重合；(4)、若数轴上M、N两点之间的距离为10（M在N的左侧），且M、N两点经过（3）中折叠后互相重合，则M、N两点表示的数分别是和.13. 如图，在长方形ABCD中，点E在AD上，连接BE、CE.将△ABE沿BE翻折得到△A′BE，△DCE 沿CE翻折得到△D'CE，分别作∠CED、∠A′BC的角平分线相交于点F.若∠BCE＝40°，∠A′ED′＝m°， 则∠BFE的度数为度 （用含m的代数式表示）.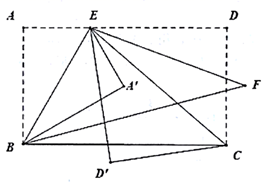
14. 如图，将长方形纸片 沿折痕EF折叠，点 ， 的对应点分别为点 ， ， 交 于点 ，再把三角形 沿 折叠，点 的对应点为点 ，若 ，则 的大小是.
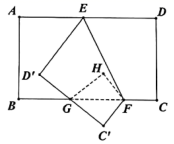15. 图1是一张足够长的纸条，其中 ，点 、 分别在 ， 上，记 .如图2，将纸条折叠，使 与 重合，得折痕 ；如图3，将纸条展开后再折叠，使 与 重合，得折痕 ：将纸条展开后继续折叠，使 与 重合，得折痕 ；...依此类推，第 次折叠后， （用含 和 的代数式表示）.
16. 如图，把一张长方形纸条ABCD沿AF折叠，点B的对应点为点E ． 已知∠ADB＝25°，AE∥BD ， 则∠BAF＝ ．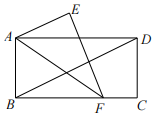
三、解答题
-
17. 如图，若 和 都是等边三角形，求 的度数．
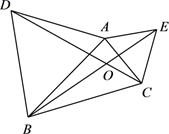18. 已知： ， ， 平分 ．求： 的度数．19. 直线EF、GH之间有一个直角三角形ABC，其中∠BAC=90°，∠ABC=α。
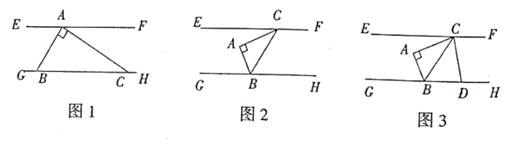(1)、如图1，点A在直线EF上，B、C在直线GH上，若∠α=60°，∠FAC=30°。试说明：EF∥GH；(2)、将三角形ABC如图2放置，直线EF∥GH，点C、B分别在直线EF、GH上，且BC平分∠ABH。求∠ECA的度数；(用α的代数式表示)(3)、在(2)的前提下，直线CD平分∠FCA交直线GH于D，如图3，在α取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化请求出变化的范围。20. 如图，把一张长方形ABCD的纸片，沿EF折叠后，ED′与BC的交点为G，点D、C分别落在D′、C′的位置上，若∠EFG=55°，求∠1、∠2的度数.
21. 如图，A点是牧马营地．每天牧马人都要从营地出发，赶着马群先到河边饮水，再到草地吃草，然后回到营地．问：怎样的放牧路线，路程最短?
22. 如图，一位小牧童，从A地出发，赶着牛群到河边饮水，然后再到B地，问应当怎样选择饮水的地点，才能使牛群所走的路线最短?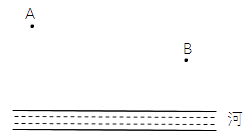
四、综合题
-
23. 如图，直线AB，CD相交于点O， ， OF平分.
(1)、写出图中所有与互补的角；(2)、若 ， 求的度数.24. 如图，直线AB与CD相交于点O，OM⊥AB于点O.(1)、如图1，若OC平分∠AOM，求∠BOD的度数；
(2)、如图2，若 ， 且平分 ， 求的度数.
25. 如图
【定义】如图1，OM平分∠AOB，则称射线OB，OA关于OM对称.
(1)、【理解题意】如图1，射线OB，OA关于OM对称且∠AOB＝45°，则∠AOM＝度；
(2)、【应用实际】如图2，若∠AOB＝45°，OP在∠AOB内部，OP，OP1关于OB对称，OP，OP2关于OA对称，求∠P1OP2的度数；
(3)、如图3，若∠AOB＝45°，OP在∠AOB外部，且0°＜∠AOP＜45°，OP，OP1关于OB对称，OP，OP2关于OA对称，求∠P1OP2的度数；(4)、【拓展提升】如图4，若∠AOB＝45°，OP，OP1关于∠AOB的OB边对称，∠AOP1＝4∠BOP1 ， 求∠AOP（直接写出答案）.
26. 如图，长方形纸片ABCD，点E，F，C分别在边AD，AB，CD上．将∠AEF沿折痕EF翻折，点A落在点A'处；将∠DEG沿折痕EG翻折，点D落在点D'处．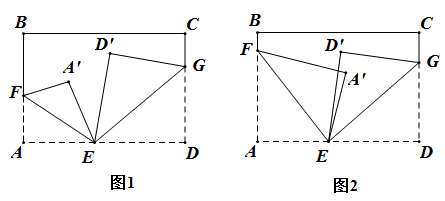
(1)、如图1，若∠AEF＝40°，∠DEG＝35°，求∠A'ED'的度数；(2)、如图1，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）；(3)、如图2，若∠A'ED'＝α，求∠FEG的度数（用含α的式子表示）．