2022年北师大数学七下期末复习阶梯训练: 生活中的轴对称(提高训练)
试卷更新日期:2022-04-08 类型:复习试卷
一、单选题
-
1. 如图,ABC中,∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC,如果BC=8cm,则DEC的周长是( )
 A、6cm B、8cm C、9cm D、10cm2. 已知长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角有( )
A、6cm B、8cm C、9cm D、10cm2. 已知长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角有( )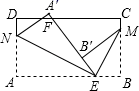 A、2个 B、3个 C、4个 D、5个3. 如图,在△ABC中, AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE的度数为( )
A、2个 B、3个 C、4个 D、5个3. 如图,在△ABC中, AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠BAC=124°,则∠DAE的度数为( ) A、68° B、62° C、66° D、56°4. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B' 处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A' 处,得折痕EN.则∠NEM的度数为( )
A、68° B、62° C、66° D、56°4. 如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B' 处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A' 处,得折痕EN.则∠NEM的度数为( )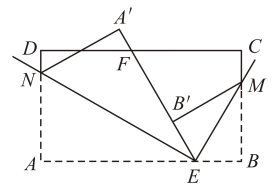 A、105o B、 C、 D、不能确定5. 如图把一张长方形的纸按如图那样折叠后,两点分别落在了点处,若= , 则的度数为( )
A、105o B、 C、 D、不能确定5. 如图把一张长方形的纸按如图那样折叠后,两点分别落在了点处,若= , 则的度数为( )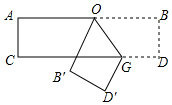 A、 B、 C、 D、6. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,则∠EDF的度数是( )
A、 B、 C、 D、6. 如图,将一张长方形纸片ABCD沿对角线BD折叠后,点C落在点E处,连接BE交AD于F,再将三角形DEF沿DF折叠后,点E落在点G处,若DG刚好平分∠ADB,则∠EDF的度数是( )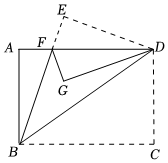 A、18° B、30° C、36° D、20°7. 如图,如果直线是△ABC的对称轴,其中∠C=66° ,那么∠BAC的度数等于( )
A、18° B、30° C、36° D、20°7. 如图,如果直线是△ABC的对称轴,其中∠C=66° ,那么∠BAC的度数等于( )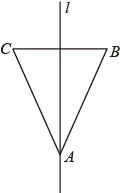 A、66° B、48° C、58° D、24°8. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )
A、66° B、48° C、58° D、24°8. 如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF=α,用含α的式子可以将∠C'FG表示为( )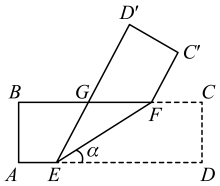 A、2α B、90°+α C、180°﹣α D、180°﹣2α9. 周长38的三角形纸片(如图甲), , 将纸片按图中方式折叠,使点A与点B重合,折痕为(如图乙),若的周长为25 , 则的长为( )
A、2α B、90°+α C、180°﹣α D、180°﹣2α9. 周长38的三角形纸片(如图甲), , 将纸片按图中方式折叠,使点A与点B重合,折痕为(如图乙),若的周长为25 , 则的长为( )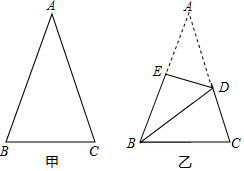 A、10 B、12 C、15 D、1310. 如图所示,有一条直的等宽纸带,按图折叠时形成一个30°的角,则重叠部分的∠α等于( )
A、10 B、12 C、15 D、1310. 如图所示,有一条直的等宽纸带,按图折叠时形成一个30°的角,则重叠部分的∠α等于( ) A、85° B、75° C、65° D、60°
A、85° B、75° C、65° D、60°二、填空题
-
11. 如图,将ABC沿着DE对折,点A落到处,若 , 则∠A=度.
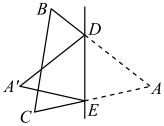 12. 如图,ABC中,直线DE是AB边的对称轴,交AC于D,交AB于E,如果BC=5,BCD的周长为15,那么AC边的长是 .
12. 如图,ABC中,直线DE是AB边的对称轴,交AC于D,交AB于E,如果BC=5,BCD的周长为15,那么AC边的长是 .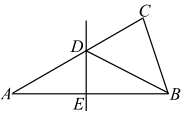 13. 将一张长方形纸条折成如图所示的形状,若 ,则 .
13. 将一张长方形纸条折成如图所示的形状,若 ,则 . 14. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在 的位置,若 ,则 等于.
14. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在 的位置,若 ,则 等于. 15. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.
15. 如图,在一条可以折叠的数轴上,A、B两点表示的数分别是 ,3,以点C为折点,将此数轴向右对折,若点A折叠后在点B的右边,且 ,则C点表示的数是.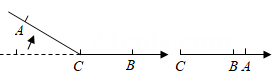 16. 如图,∠AOB内一点P,P1、P2分别是点P关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是 .
16. 如图,∠AOB内一点P,P1、P2分别是点P关于OA、OB的对称点,P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长是 .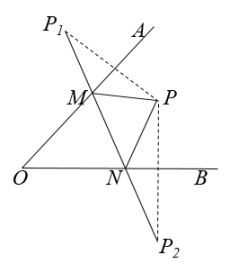
三、解答题
-
17. 如图,△ABC中,∠BAC=90°,点D是BC上的一点,将△ABC沿AD翻折后,点B恰好落在线段CD上的B'处,且AB'平分∠CAD.求∠BAB'的度数.
 18. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长.
18. 如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E,连接BD.若AE=6,△CBD的周长为20,求BC的长. 19. 在中,AB=AC, , AB的垂直平分线交BC于M,交AB与E,AC的垂直平分线交BC 于N ,交AC于F,求证:BM=MN=NC.
19. 在中,AB=AC, , AB的垂直平分线交BC于M,交AB与E,AC的垂直平分线交BC 于N ,交AC于F,求证:BM=MN=NC. 20. 在一个等腰三角形中,一条边是3a+2b,另一条边是2a-2,那么这个等腰三角形的周长是多少?21. 如图,在 中, , 是 中点, ,垂足为 .若 ,求 的度数.
20. 在一个等腰三角形中,一条边是3a+2b,另一条边是2a-2,那么这个等腰三角形的周长是多少?21. 如图,在 中, , 是 中点, ,垂足为 .若 ,求 的度数. 22. 如图,在 ABC中,∠B=90°,∠A=30°.作边AC的垂直平分线交AB于点D , 交AC于点E , 连接CD , 已知BD=4,求∠BCD的度数及AD的长.
22. 如图,在 ABC中,∠B=90°,∠A=30°.作边AC的垂直平分线交AB于点D , 交AC于点E , 连接CD , 已知BD=4,求∠BCD的度数及AD的长.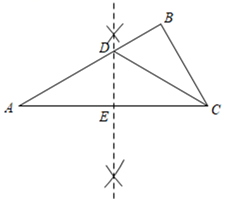
四、综合题
-
23. 如图,点O在直线AB上, , 和互补.
 (1)、根据已知条件,可以判断 , 将如下推理过程补充完整(括号内填推理依据).
(1)、根据已知条件,可以判断 , 将如下推理过程补充完整(括号内填推理依据).推理过程:因为和互补,
所以 ▲ °.( ▲ ),
因为点O在直线AB上,所以 .
所以 ,
所以 . ( ▲ )
(2)、求的度数.24. 作图并计算:如图,点O在直线上. (1)、画出的平分线(不必写作法);(2)、在(1)的前提下,若 , 求的度数.25. 如图为10×10的正方形网格,每个小正方形的边长均为1,小正方形的顶点叫做格点,顶点在格点上的三角形叫做格点三角形.已知△ABC是格点三角形,
(1)、画出的平分线(不必写作法);(2)、在(1)的前提下,若 , 求的度数.25. 如图为10×10的正方形网格,每个小正方形的边长均为1,小正方形的顶点叫做格点,顶点在格点上的三角形叫做格点三角形.已知△ABC是格点三角形,按要求解决下列问题:
 (1)、请直接写出△ABC的面积;(2)、①以AC为一边,在AC的下方画一个格点△ACD , 使它与△ABC成轴对称,并画出对称轴m;
(1)、请直接写出△ABC的面积;(2)、①以AC为一边,在AC的下方画一个格点△ACD , 使它与△ABC成轴对称,并画出对称轴m;②以点B为顶点画一个格点△BEF , 使它与△ABC全等且仅有一个公共顶点B .
26. 如图,已知点A在数轴上,从点A出发,沿数轴向右移动3个单位长度到达点C , 点B所表示的有理数是 -3的相反数,按要求完成下列各小题. (1)、请在数轴上标出点B和点C;(2)、求点B所表示的有理数与点C所表示的有理数的乘积;(3)、若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.
(1)、请在数轴上标出点B和点C;(2)、求点B所表示的有理数与点C所表示的有理数的乘积;(3)、若将该数轴进行折叠,使得点A和点B重合,则点C和数 所表示的点重合.