2022年北师大数学七下期中复习阶梯训练：三角形（优生集训）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、综合题

1. 已知△ABC和△ADE都是等腰直角三角形，点D是直线BC上的一动点（点D不与B、C重合），连接CE，

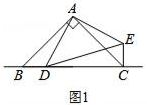
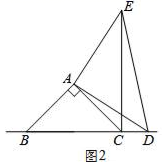
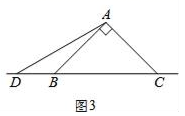(1)、在图1中，当点D在边BC上时，求证：BC=CE+CD；

(2)、在图2中，当点D在边BC的延长线上时，结论BC=CE+CD是否还成立？若不成立，请猜想BC、CE、CD之间存在的数量关系，并说明理由；

(3)、在图3中，当点D在边BC的反向延长线上时，补全图形，不需写证明过程，直接写出BC、CE、CD之间存在的数量关系．

查看试题解析
2. 如图1，直角三角形DEF与直角三角形ABC的斜边在同一直线上， $∠ C = ∠ E = 90 °$ ， $∠ E D F = 30 °$ ， $∠ A B C = 40 ° .$ 如图2，连接CD，CD平分 $∠ A C B$ ，将 $△ D E F$ 绕点D按逆时针方向旋转，记 $∠ A D F$ 为 $α (0 ° < α < 180 °)$ .

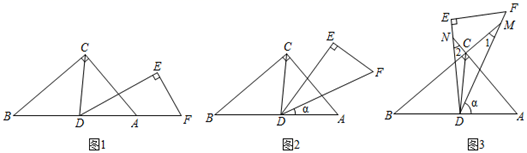(1)、 $∠ C D A$ 的度数为 .

(2)、如图3，在旋转过程中，当顶点C在 $△ D E F$ 内部时，边DF，DE分别交BC，AC的延长线于点M，N.
①求 $α$ 的度数范围；

② $∠ 1$ 与 $∠ 2$ 度数的和是否变化？若不变，请求出 $∠ 1$ 与 $∠ 2$ 的度数和；若变化，请说明理由.

查看试题解析
3. $△ A B C$ （ $∠ C > 90 °$ ）的三条角平分线相交于点 $D$ ，延长 $A D$ 交 $B C$ 于点 $E$ ．作 $A F ⊥ B C$ ，交 $B C$ 延长线于点 $F$ ．

(1)、若 $∠ B A C = 40 °$ ，则 $∠ B D C =$ ；

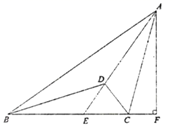(2)、判断 $∠ C D E$ 与 $∠ A B D$ 的数量关系，并说明理由；

(3)、求证 $∠ A C D = ∠ E A F + ∠ A B D$ ．

查看试题解析
4. 综合与探究：问题情景：如图1所示，已知，在△ABC中，AC＝BA，∠ACB＝90°，AD是△ABC的中线，过点C作CE⊥AD，垂足为M，且交AB于点E．

(1)、（探究一）小虎通过度量发现∠BCE＝∠CAD，请你帮他说明理由；

(2)、（探究二）小明在图中添加了一条线段CN，且CN平分∠ACB交AD于点N，如图2所示，即可得CN＝BE，符合题意吗？请说明理由；

(3)、（探究三）小刚在（2）的基础上，连接DE，如图3所示，又发现了一组全等三角形，你能发现吗？请找出来，并说明理由．

查看试题解析
5. 如图1，△ABC为等边三角形，三角板的60°角顶点与点C重合，三角板的一直角边与AB交于点D，在三角板斜边上取一点F，使CF＝CD，线段AB上取点E，使∠DCE＝30°，连接AF、EF．

(1)、求证：△ACF≌△BCD；

(2)、写出线段DE与EF之间的数量关系，并说明理由；

(3)、如图2，若△ABC为等腰直角三角形，∠ACB＝90°，三角板的90°角顶点与点C重合，三角板的一直角边与AB交于点D，在三角板另一直角边上取一点F，使CF＝CD，在线段AB上取点E，使∠DCE＝45°，连接AF、EF．求∠EAF．

查看试题解析
6. 如图1，∠ABC＝90°，FA⊥AB于点A，D是线段AB上的点，AD＝BC，AF＝BD．

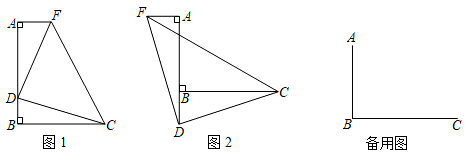(1)、判断DF与DC的数量关系为，位置关系为．

(2)、如图2，若点D在线段AB的延长线上，过点A在AB的另一侧作AF⊥AB，并截取AF＝BD，连接DC、DF、CF，试说明（1）中结论是否成立，并说明理由．

(3)、若点D在线段AB外，点E是BC延长线上一点，且CE＝BD，连接AE，与DC的延长线交于点P，直接写出∠APC的度数．

查看试题解析
7. 【探究】如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．

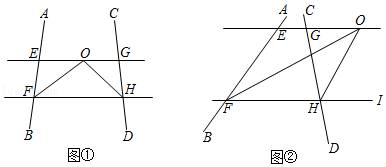(1)、若∠AFH＝60°，∠CHF＝50°，则∠EOF＝度，∠FOH＝度．

(2)、若∠AFH+∠CHF＝100°，求∠FOH的度数．

(3)、【拓展】如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．（用含a的代数式表示）

查看试题解析
8. 已知AM∥CN，点B为平面内一点，AB⊥BC于B．(温馨提示：本题可能用到知识点：三角形三角和为180°)

(1)、如图1，若∠A=40°，求∠C的度数；

(2)、如图2，过点B作BD⊥AM于点D，说明：∠ABD=∠C；

(3)、如图3，在(2)问的条件下，点E、F在射线DM上，连结BE、BF、CF，BF平分∠DBC，BE平分∠ABD，若∠FCB+∠NCF= 180° ，∠BFC=3∠DBE，求∠EBC的度数。

查看试题解析
9. 直线 $M N$ 与直线 $P Q$ 垂直相交于 $O$ ，点 $A$ 在直线 $P Q$ 上运动，点 $B$ 在直线 $M N$ 上运动.

(1)、如图1，已知 $A E$ ， $B E$ 分别是 $∠ B A O$ 和 $∠ A B O$ 角的平分线，点 $A$ 、 $B$ 在运动的过程中， $∠ A E B$ 的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出 $∠ A E B$ 的大小.

(2)、如图2，已知 $A B$ 不平行 $C D$ ， $A D$ 、 $B C$ 分别是 $∠ B A P$ 和 $∠ A B M$ 的角平分线，又 $D E$ 、 $C E$ 分别是 $∠ A D C$ 和 $∠ B C D$ 的角平分线，点 $A$ 、 $B$ 在运动的过程中， $∠ C E D$ 的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值.

(3)、如图3，延长 $B A$ 至 $G$ ，已知 $∠ B A O$ ， $∠ O A G$ 的角平分线与 $∠ B O Q$ 的角平分线及延长线相交于 $E$ 、 $F$ ，在 $△ A E F$ 中，如果有一个角是另一个角的3倍，直接写出 $∠ A B O$ 的度数 $=$ .

查看试题解析
10. 某学习小组发现一个结论：已知直线a//b，若直线c//a，则c//b，他们发现这个结论运用很广，请你利用这个结论解决以下问题：
已知直线AB//CD，点E在AB，CD之间，点P，Q分别在直线AB，CD上，连接PE，EQ．

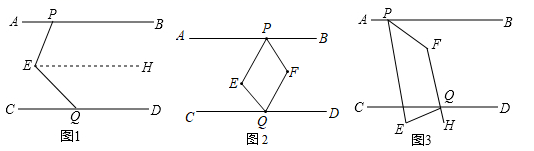(1)、如图1，作EH//AB，运用上述结论，探究∠PEQ与∠APE+∠CQE间的数量关系，并说明理由；

(2)、如图2，PF平分∠BPE，QF平分∠EQD，当∠PEQ=130º时，求出∠PFQ的度数；

(3)、如图3，若点E在CD的下方，PF平分∠BPE，QH平分∠EQD，QH的反向延长线交PF于点F，当∠PEQ=80º时，直接写出∠PFQ的度数．

查看试题解析
11. 如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”.

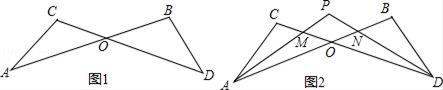(1)、求证：∠A+∠C＝∠B+D；

(2)、如图2，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有_▲_个，以点O为交点的“8字型”有_▲_个；

②若∠B＝100°，∠C＝120°，求∠P的度数；

③若角平分线中角的关系改为“∠CAP＝ $\frac{1}{3}$ ∠CAB，∠CDP＝ $\frac{1}{3}$ ∠CDB”，试探究∠P与∠B、∠C之间存在的数量关系，并证明理由.

查看试题解析
12. 如图，在△ABC中，BD、CD分别平分∠ABC、∠ACB，点M、N、Q分别在AB、AC、BC的延长线上，BE、CE分别平分∠MBC、∠NCB.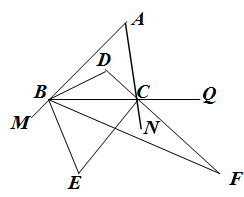

(1)、若∠A＝60°
①∠BDC的度数为 .

②求∠BEC的度数.

(2)、如图，若在∠EBC内部作∠EBF，使 $∠ E B F = \frac{2}{3} ∠ E B C$ ，在∠ECQ内部作∠ECF，使 $∠ E C F = \frac{2}{3} ∠ E C Q$ ，则∠BEC和∠BFC有什么样的数量关系？请简述理由.

查看试题解析
13. 已知AB∥CD，CF平分∠ECD.

(1)、如图1，若∠DCF=25°，∠E=20°，求∠ABE的度数.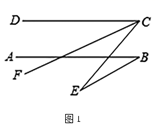

(2)、如图2，若∠EBF=2∠ABF，∠CFB的2倍与∠CEB的补角的和为190°，求∠ABE的度数.

查看试题解析
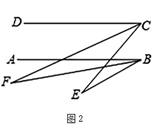14. 如图1，直角三角形DEF与直角三角形ABC的斜边在同一直线上，∠EDF＝30°，∠ABC＝40°，CD平分∠ACB，将△DEF绕点D按逆时针方向旋转，记∠ADF为α（0°＜α＜180°），在旋转过程中；

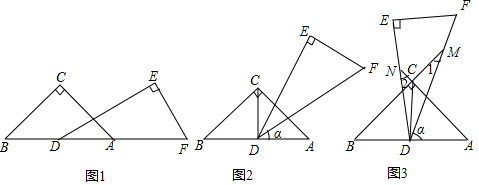(1)、如图2，当∠α＝时， $D E // B C$ ，当∠α＝时，DE⊥BC；

(2)、如图3，当顶点C在△DEF内部时，边DF、DE分别交BC、AC的延长线于点M、N，
①此时∠α的度数范围是 ▲ ；

②∠1与∠2度数的和是否变化？若不变求出∠1与∠2度数和；若变化，请说明理由；

③若使得∠2≥2∠1，求∠α的度数范围.

查看试题解析
15. 如图（1）四边形ABCD中，已知∠ABC+∠ADC=180°，AB=AD，DA⊥AB，点E在CD的延长线上，∠BAC=∠DAE．

(1)、试说明：△ABC≌△ADE；

(2)、试说明CA平分∠BCD；

(3)、如图（2），过点A作AM⊥CE，垂足为M，试说明：∠ACE=∠CAM=∠MAE=∠E=45°．

查看试题解析
16. 如图，已知∠BDC＋∠EFC＝180°，∠DEF＝∠B.

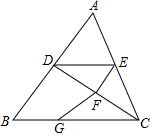(1)、求证：ED∥BC；

(2)、若D，E，F分别是AB，AC，CD边上的中点，四边形ADFE的面积为6.
①求△ABC的面积；
②若G是BC边上一点，CG＝2BG，求△FCG的面积.

查看试题解析
17. 数学问题：如图，在 $△ A B C$ 中， $∠ A = 20^{\circ} ， ∠ A B C ， ∠ A C B$ 的 $2020$ 等分线分别交于点 $O_{1} ， O_{2} ， ..... ， O_{10} ， O_{2020} ，$ 根据 $2020$ 等分线等分角的情况解决下列问题：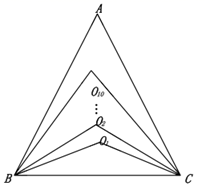

(1)、求 $∠ B O_{1} C$ 的度数.

(2)、求 $∠ B O_{3} C$ 的度数.

(3)、直接写出 $∠ B O_{2020} C$ 的度数.

查看试题解析
18. △ABC中，AD是∠BAC的角平分线，AE是△ABC的高.

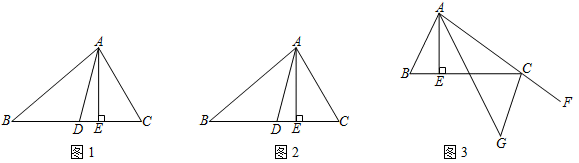(1)、如图1，若∠B＝40°，∠C＝62°，请说明∠DAE的度数；

(2)、如图2（∠B＜∠C），试说明∠DAE、∠B、∠C的数量关系；

(3)、如图3，延长AC到点F，∠CAE和∠BCF的角平分线交于点G，求∠G的度数.

查看试题解析
19. 如图①，已知AB//CD， AC//EF

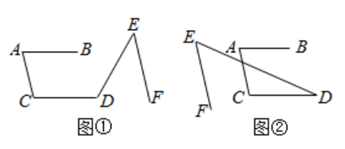(1)、若∠A=75°， ∠E=45°，求∠C和∠CDE的度数；

(2)、探究：∠A、∠CDE与∠E之间有怎样的等量关系？并说明理由.

(3)、若将图①变为图②，题设的条件不变，此时∠A、∠CDE 与∠E之间又有怎样的等量关系，请直接写出你探究的结论.

查看试题解析
20. 已知 $△$ ABC，P 是平面内任意一点（A、B、C、P 中任意三点都不在同一直线上）.连接 PB、PC，设∠PBA＝s°，∠PCA＝t°，∠BPC＝x°，∠BAC＝y°.

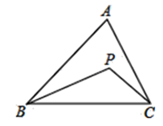(1)、如图，当点 P 在 $△$ ABC 内时，
①若 y＝70，s＝10，t＝20，则 x＝；

②探究 s、t、x、y 之间的数量关系，并证明你得到的结论.

(2)、当点 P 在 $△$ ABC 外时，直接写出 s、t、x、y 之间所有可能的数量关系，并画出相应的图形.

查看试题解析
21. 综合探究：
如图，在 $△ A B C$ 中， $B D ， C E$ 分别是 $A C ， A B$ 边上的高，在 $B D$ 上截取 $B F = A C ，$ 延长 $C E$ 至点 $G$ 使 $C G = A B$ ，连接 $A F ， A G$ ．

(1)、如图1中， $A G$ 与 $A F$ 相等吗？为什么？

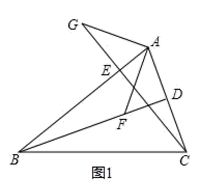(2)、如图2，若BD恰好平分 $∠ A B C$ ，过点 $G$ 作 $G H ⊥ A C$ 交 $C A$ 的延长线于点 $H$ 请直接写出图中所有的全等三角形并用全等符号连接．

查看试题解析
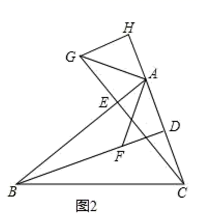22. 当光线经过镜面反射时，入射光线、反射光线与镜面所夹的角对应相等.例如：在图①、图②中，都有∠1＝∠2，∠3＝∠4.设镜子AB与BC的夹角∠ABC＝α.

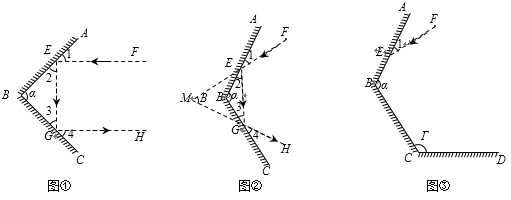(1)、如图①，若 $α$ ＝90°，判断入射光线EF与反射光线GH的位置关系，并说明理由.

(2)、如图②，若90°＜ $α$ ＜180°，入射光线EF与反射光线GH的夹角∠FMH＝ $β$ .探索 $α$ 与 $β$ 的数量关系，并说明理由.

(3)、如图③，若 $α$ ＝120°，设镜子CD与BC的夹角∠BCD＝γ(90°＜γ＜180°)，入射光线EF与镜面AB的夹角∠1＝m(0°＜m＜90°).已知入射光线EF从镜面AB开始反射，经过n(n为正整数，且n≤3)次反射，当第n次反射光线与入射光线EF平行时，请直接写出γ的度数.（可用含有m的代数式表示）

查看试题解析
23. 将锐角 $Δ A B C$ 放置在一块正方形卡纸 $D E F G$ 上，使点 $B ， C$ 在正方形的 $D G$ 和 $D E$ 边上．

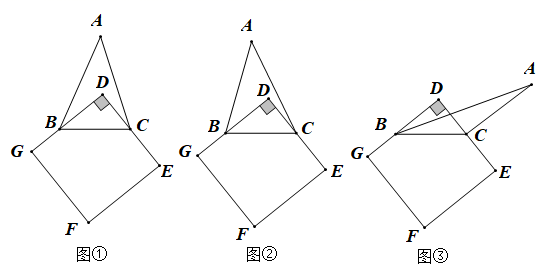(1)、如图①，若 $∠ A = 35 °$ ，则 $∠ A B C + ∠ A C B =$ 度， $∠ D B C + ∠ D C B =$ 度， $∠ A B D + ∠ A C D =$ 度．

(2)、如图②，改变正方形卡纸 $D E F G$ 的位置，请探究 $∠ A B D + ∠ A C D$ 与 $∠ A$ 之间存在怎样的数量关系，并验证你的结论．

(3)、如图③，正方形卡纸的顶点 $D$ 在 $△ A B C$ 外，且在 $A B$ 边的左侧，请探究 $∠ A B D ， ∠ A C D$ ， $∠ A$ 三者之间存在怎样的数量关系，直接写出探究结果，不必验证．

查看试题解析
24. 如图

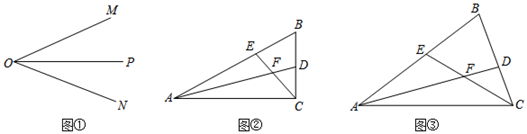(1)、如图①，OP是 $∠ M O N$ 的平分线，请你在OP上取一点A，利用该图画一对以OP所在直线为对称轴的两个全等三角形(保留画图痕迹 )；

(2)、如图②，在 $△ A B C$ 中， $∠ A C B$ 是直角， $∠ B = 60 ° ， A D ， C E$ 分别是 $∠ B A C ， ∠ B C A$ 的平分线，AD、CE相交于点F，求 $∠ E F A$ 的度数，并判断FE与FD之间的数量关系，并说明道理；

(3)、如图③，在 $△ A B C$ 中，如果 $∠ A C B$ 不是直角，而 (1)中的其它条件不变，请问：你在（2）中所得结论是否仍然成立?若成立，请证明：若不成立，请说明理由．

查看试题解析
25. 如图，四边形ABCD中，AB∥CD，∠B＝∠D，点E为BC延长线上一点，连接AE，AE交CD于H.∠DCE的平分线交AE于G.

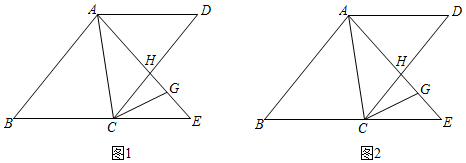(1)、求证：AD∥BC；

(2)、若∠BAC＝∠DAE，∠AGC＝2∠CAE.求∠CAE的度数；

(3)、（2）中条件∠BAC＝∠DAE仍然成立，若∠AGC＝3∠CAE，直接写出∠CAE的度数.

查看试题解析
26. 如图1，直线MN与直线AB、CD分别交于点E、F ， ∠1与∠2互补．

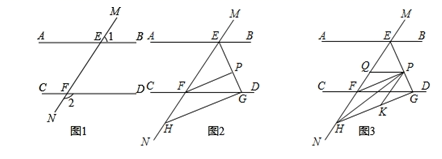(1)、试判断直线AB与直线CD的位置关系，并说明理由；

(2)、如图2，∠BEF与∠EFD的角平分线交于点P ， EP与CD交于点G ，点H是MN上一点，且GH⊥EG ，求证：PF∥GH；

(3)、如图3，在（2）的条件下，连接PH ， K是GH上一点使∠PHK=∠HPK ，作PQ平分∠EPK ，求∠HPQ的度数．

查看试题解析