2022年北师大数学七下期中复习阶梯训练：三角形（优生加练）
试卷更新日期：2022-04-08 类型：复习试卷
一、单选题
-
1. 如图，在△AOB和△COD中，OA＝OB ， OC＝OD ， OA＜OC ， ∠AOB＝∠COD＝36°．连接AC ， BD交于点M ， 连接OM ． 下列结论：
①∠AMB＝36°，②AC＝BD ， ③OM平分∠AOD ， ④MO平分∠AMD ． 其中正确的结论个数有（ ）个．
A、4 B、3 C、2 D、12. 将一副三角板按如图放置，有下列结论：①若∠2=30°，则AC∥DE；②∠BAE+∠CAD=180°；③若BC∥AD，则∠2=30°；④若∠CAD=150°，则
∠4=∠C.其中正确的是（ ）
A、①②④ B、①③④ C、②③④ D、①②③④3. 如图，AD∥BC，∠D＝∠ABC，点E是边DC上一点，连接AE交BC的延长线于点H，点F是边AB上一点，使得∠FBE＝∠FEB，作∠FEH的角平分线EG交BH于点G.若∠BEG＝40°，则∠DEH的度数为（ ）
A、50° B、75° C、100° D、125°4. 如图，已知AC平分∠DAB，CE⊥AB于E，AB=AD+2BE，则下列结论：①AB+AD=2AE；②∠DAB+∠DCB=180°；③CD=CB；④S△ACE﹣2S△BCE=S△ADC；其中符合题意结论的个数是（ ）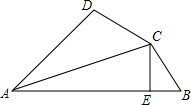
A、1个 B、2个 C、3个 D、4个5. 如图，点P在∠MAN的角平分线上，点B，C分别在AM，AN上，作PR⊥AM，PS⊥AN，垂足分别是R，S．若∠ABP+∠ACP=180°，则下面三个结论：①AS=AR；②PC∥AB；③△BRP≌△CSP．其中正确的是（ ）
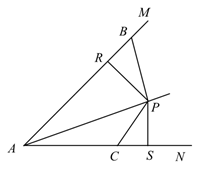A、①② B、②③ C、①③ D、①②③6. 如图， ， 与 的平分线相交于点 ， 于点 ， 为 中点， 于 ， ．下列说法正确的是（ ）① ；② ；③ ；④若 ，则 ．
A、①③④ B、②③ C、①②③ D、①②③④7. 如图，下列四个条件： ①BC＝B′C；②AC＝A′C；③∠A′CA＝∠B′CB；④AB＝A′B′.从中任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（ ）
A、1 B、2 C、3 D、48.如图在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS，AB=AC，下面三个结论：①AS=AR；②PQ∥AB；③△BRP≌△CSP，其中正确的是（ ）
A、①② B、②③ C、①③ D、①②③9. 如图，是三个等边三角形（注：等边三角形的三个内角都相等）随意摆放的图形，则 等于（ ）
A、90° B、120° C、150° D、180°10. 在下列四组条件中，能判定△ABC≌△DEF的是（ ）A、AB=DE ， BC= EF ， ∠A=∠D B、∠A=∠D ， ∠C=∠F ， AC= DE C、∠A=∠E ， ∠B=∠F ， ∠C=∠D D、AB=DE ， BC= EF ， △ABC的周长等于△DEF的周长二、填空题
-
11. 如图，已知 ，点 在 上，点 为平面内一点， ，过点 作 平分 平分 ，若 ，则 .
12. 如图1是一个消防云梯，其示意图如图2所示，此消防云梯由救援台AB，延展臂BC（B在C的左侧），伸展主臂CD，支撑臂EF构成，在操作过程中，救援台AB，车身GH及地面MN三者始终保持平行．当∠EFH=55°，BC∥EF时，∠ABC=度；如图3，为了参与另外一项高空救援工作，需要进行调整，使得延展臂BC与支撑臂EF所在直线互相垂直，且∠EFH=78°，则这时∠ABC= 度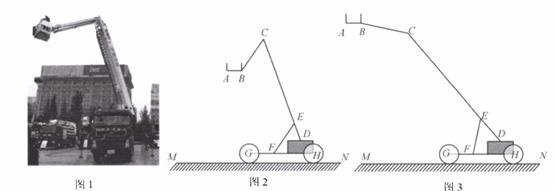
13. 如图，点C在线段AB上，DA⊥AB ， EB⊥AB ， FC⊥AB ， 且DA＝ BC ， EB＝AC ， FC＝AB ， ∠AFB＝50°，则∠DFE＝ ．
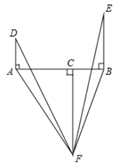14. 如图，△DAC和△EBC均是等边三角形，A、C、B三点共线，AE与BD相交于点P ， AE与BD分别与CD、CE交于点M、N ， 有如下结论：①△ACE≌△DCB；②∠DPA＝60°；③AC＝DN；④EM＝BN；⑤DC∥EB ， 其中正确结论是（填序号）
15. 如图，在四边形 中， ， ， 于点 ， 于点 ， 、 分别是 、 上的点，且 ，下列说法正确的是.（填写正确的序号）① ，② ，③ 平分 ，④ 平分 ，⑤ ，⑥ .
16. 如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，其中点C，D，E在同一条直线上，连接BD，BE。以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④∠ACE=∠DBC正确的是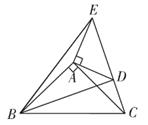
三、解答题
-
17. 如图，在 和 中，点 、 、 、 在同一直线上，请你从以下4个等式中选出3个作为已知条件，余下的1个作为结论，并说明结论正确的理由（写出各种可能的情况，并选择其中一种说理）．
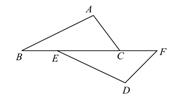
① ；② ；③ ；④ ．
18. 如图，已知△ABC≌△ADE，AB与ED交于点M，BC与ED，AD分别交于点F，N.请写出图中两对全等三角形(△ABC≌△ADE除外)，并选择其中的一对加以说明．
19. 如图，已知DA⊥AB，DE平分∠ADC，CE平分 ∠BCD， ∠1+ ∠2=90°．求证：BC ⊥ AB．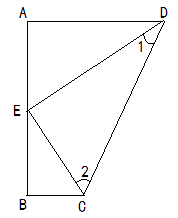
20. 如图所示，在 △ ABC中， ∠ABC=∠C，BD⊥AC交AC于D．求证： ∠DBC= ∠A．
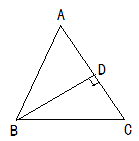21. 如图，求 ∠A+∠B+∠C+∠D+∠E的大小．
22. 如图，AB、CD相交于E，CF、BF分别为 ∠ACD和 ∠ABD的平分线，它们相交于F．求证：∠F= ( A+D)．
四、综合题
-
23. 如图，已知点E，F在直线AB上，点 在线段CD上，ED与FG交于点 .
(1)、求证： .(2)、试判断 与 之间的数量关系，并说明理由.(3)、若 ，求 的度数.24. 如图，在同一平面内，点D、E是△ABC外的两点，请按要求完成下列问题．（此题作图不要求写出画法）
(1)、请你判断线段与AC的数量关系是 ， 理由是 ．(2)、连接线段CD，作射线BE、直线DE，在四边形BCDE的边BC、CD、DE、EB上任取一点，分别为点K、L、M、N并顺次连接它们，则四边形KLMN的周长与四边形BCDE周长哪一个大，直接写出结果（不用说出理由）．(3)、在四边形KLMN内找一点O，使它到四边形四个顶点的距离之和最小（作图找到点即可）．25. 如图所示，已知射线CB∥OA，∠C=∠OAB=100°，E，F在CB上，且满足∠FOB=∠AOB，OE平分∠COF．
(1)、求∠EOB的度数；(直接写出结果)(2)、若在0C右侧左右平行移动AB，那么∠OBC：∠OFC的值是否随之发生变化？若变化，请找出变化的规律；若不变，请求出这个比值；(3)、在OC右侧左右平行移动AB的过程中，是否存在使∠OEC=∠OBA的情况？若存在，请直接写出∠OEC的度数；若不存在，请说明理由．26. 已知CD是经过∠BCA顶点C的一条直线，CA=CB ． E、F分别是直线CD上两点，且∠BEC=∠CFA=∠ ．
(1)、若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：①如图1若∠BCA=90°，∠ =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2，若0°＜∠BCA＜180°， 请添加一个关于∠ 与∠BCA关系的条件，使①中的结论仍然成立；
(2)、如图3，若直线CD经过∠BCA的外部，∠ =∠BCA ， 请写出三条线段EF、BE、AF的数量关系并证明你的结论.