2022年初中数学苏科版《中考二轮复习》 专题一 数与式、方程与不等式 1.5 一元一次方程
试卷更新日期:2022-04-08 类型:二轮复习
一、单选题
-
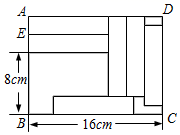
1. 在解方程 时,去分母后正确的是( )A、 B、 C、 D、2. 若方程:2(x-1)-6=0与的解互为相反数,则a的值为( )A、 B、 C、 D、-13. 期定期储蓄年利率为2.25%,按照国家规定,所得利息要缴纳20%的利息税,王大爷于2004年6月存入银行一笔钱,一年到期时,共得税后利息540元,则王大爷2004年6月的存款额为( )A、24 000元 B、30 000元 C、12 000元 D、15 000元4. 某品牌服装店一次同时售出两件上衣,每件售价都是150元,若按成本计算,其中一件盈利25%,另一件亏损25%,则这家商店在这次销售过程中( )A、盈利为0 B、盈利为20元 C、亏损为18元 D、亏损为20元5. 甲、乙两名同学从学校出发到国色天香游乐园,甲每小时走4km,乙每小时走6km,甲出发一个小时后乙才出发,结果乙比甲早到20分钟,若设学校到游乐园的距离为xkm,则下列方程正确的是( )A、+1=﹣20 B、+1= C、﹣1= D、﹣1=﹣6. 在长方形ABCD中放入六个相同的小长方形,所标尺寸如图所示,求小长方形的宽AE.若设AE=x(cm),依题意可得方程( )
 A、16﹣3x=8 B、8+2x=16﹣3x C、8+2x=16﹣x D、8+2x=x+(16﹣3x)7. 某城市倡导节约型社会,鼓励节约能源,家庭使用管道煤气收费标准为每户每月煤气用量不超过60立方米,按每立方米0.8元收费;如果超过60立方米.超过部分按每立方米1.2元收费,已知小聪家12月份的煤气费为60元,则小聪家12月份的煤气用量为( ).A、49立方米 B、61立方米 C、70立方米 D、71立方米8. 某铁路桥长1200m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.则火车的长度为( )A、180m B、200m C、240m D、250m9. 某公司出售A,B,C三种商品,前一阶段结帐时,商品C的售出金额高达总金额的60%,预计目前阶段A,B两种商品售出金额要比前一阶段减少5%,因而商品C更是推销重点,要想使现阶段售出的总金额比前一阶段增长10%,必须努力使商品C的售出金额比前阶段增加百分之( )A、20 B、25 C、30 D、3510. 如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )
A、16﹣3x=8 B、8+2x=16﹣3x C、8+2x=16﹣x D、8+2x=x+(16﹣3x)7. 某城市倡导节约型社会,鼓励节约能源,家庭使用管道煤气收费标准为每户每月煤气用量不超过60立方米,按每立方米0.8元收费;如果超过60立方米.超过部分按每立方米1.2元收费,已知小聪家12月份的煤气费为60元,则小聪家12月份的煤气用量为( ).A、49立方米 B、61立方米 C、70立方米 D、71立方米8. 某铁路桥长1200m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.则火车的长度为( )A、180m B、200m C、240m D、250m9. 某公司出售A,B,C三种商品,前一阶段结帐时,商品C的售出金额高达总金额的60%,预计目前阶段A,B两种商品售出金额要比前一阶段减少5%,因而商品C更是推销重点,要想使现阶段售出的总金额比前一阶段增长10%,必须努力使商品C的售出金额比前阶段增加百分之( )A、20 B、25 C、30 D、3510. 如图,往竖直放置的在A处由短软管连接的粗细均匀细管组成的“U”形装置中注入一定量的水,水面高度为6cm,现将右边细管绕A处顺时针旋转60°到AB位置,且左边细管位置不变,则此时“U”形装置左边细管内水柱的高度约为( )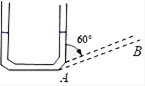 A、4cm B、2 cm C、3cm D、8cm
A、4cm B、2 cm C、3cm D、8cm二、填空题
-
11. 定义一种新运算“ ”规则如下:对于两个有理数a,b, ,若 ,则12. 将一堆糖果分给幼儿园的小朋友,如果每人2颗,那么就多8颗;如果每人3颗,那么就少12颗.设幼儿园里有x个小朋友,可得方程.13. A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发相向而行,已知甲车速度为120千米/时,乙车速度为80千米/时,经过 小时两车相距50千米.14. 扬州雕版印刷技艺历史悠久,元代数学家朱世杰的《算学启蒙》一书曾刻于扬州,该书是中国较早的数学著作之一,书中记载一道问题:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之?”题意是:快马每天走240里,慢马每天走150里,慢马先走12天,试问快马几天追上慢马?答:快马天追上慢马.15. 如图,有一根木棒 放置在数轴上,它的两端M、N分别落在点A、B.将木棒在数轴上水平移动,当点M移动到点B时,点N所对应的数为20,当点N移动到点A时,点M所对应的数为5(单位: ),则木棒 长为 .
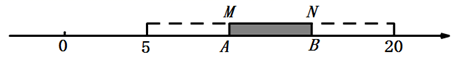 16. 一列火车正在匀速行驶,它先用25秒的时间通过了长300米的隧道甲(即从火车头进入入口到车尾离开出口),又用16秒的时间通过了长120米的隧道乙,下列说法正确的是.(填番号)
16. 一列火车正在匀速行驶,它先用25秒的时间通过了长300米的隧道甲(即从火车头进入入口到车尾离开出口),又用16秒的时间通过了长120米的隧道乙,下列说法正确的是.(填番号)①这列火车长150米;②这列火车的行驶速度为10米每秒;
③若保持原速度不变,则这列火车通过长160米的隧道丙需用时18秒;
④若速度变为原速度的两倍,则这列火车通过隧道甲的时间将变为原来的一半.
17. 某超市推出如下优惠方案:①一次性购物不超过100元不享受优惠;
②一次性购物超过100元但不超过300元,一律9折
③一次性购物超过300元,一律8折
小李两次购物分别付款80元,252元,如果他一次性购买以上两次相同的商品,应付款
18. 甲乙二人在环形跑道上同时同地出发,同向运动,若甲的速度是乙的速度的2倍,则乙运动1周,甲、乙第一次相遇;若甲的速度是乙的速度的3倍,则乙运动 周,甲、乙第一次相遇;若甲的速度是乙的速度的4倍,则乙运动 周,甲、乙第一次相遇;……以此探究正常走时的时钟,时针和分针从重叠位置同时出发,时针旋转周,时针和分针第一次相遇.三、解答题
-
19.(1)、﹣3x+7=4x+21;(2)、 ﹣1= +x;20. 小明在对关于 的方程 去分母时,得到了方程 ,因而求得的解是 ,你认为他的答案正确吗?如果不正确,请求出原方程的正确解.21. 甲、乙两家超市以相同的价格出售同样的商品.为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出 元之后,超出部分按原价八折优惠;在乙超市累计购买商品超出 元之后,超出部分按原价九折优惠.设顾客预计累计购物x元 ,试比较顾客到哪家超市购物更优惠?说明你的理由.22. 某公司以每吨500元的价格收购了100吨某种药材,若直接在市场上销售,每吨的售价为1000元,该公司决定加工后再出售,相关信息如下表所示:
工艺
每天可加工药材的吨数
出品率
售价(元/吨)
粗加工
14
80%
5000
精加工
6
60%
11000
注:①出品率本指加工后所得产品的质量与原料的重量的比值,②加工后的废品不产生效益,
受市场影响,请公司必须在10天内将这批药材加工完毕,现有3种方案:
A.全部粗加工,则获利多少元?
B尽可能多的精加工,剩余的直接在市场上销售,则可获利多少元;
C部分粗加工,部分精加工,恰好10天完成,可获利多少元?
问:哪个方案获得的利润最大?是多少?
23. 甲、乙两个工程队第一次合作完成6000米的公路修建工程,两队的修建速度及每天所需工程费的情况如表所示,最终甲队的工作天数比乙队的工作天数的2倍少20天.甲
乙
修建速度(米/天)
90
80
每天所需工程费(元)
1200
1000
(1)、甲、乙两队分别工作了多少天?完成该项工程甲、乙两队所需工程费各多少元?(2)、甲、乙两个工程队第二次又合作完成某项公路修建工程,其中乙队分到的工作量是它的第一次的2倍,同时由于乙队减少了人员和设备,修建速度比它的第一次减少了25%,每天所需工程费也因此而打折.完成该项任务后,乙队所需工程费比它的第一次多了38000元,求乙队第二次每天所需工程费是它的第一次的几折?24. 如图,甲、乙两人(看成点)分别在数轴﹣3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.
 (1)、若两人完成了2次移动游戏第一次甲、乙都错,第二次甲对乙错,此时甲、乙两人的距离为;(2)、从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,则他最终停留的位置对应的数是什么?试用含n的代数式表示,并求该位置距离原点O最近时n的值;(3)、从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.25. 如图,数轴上点A表示的数为-3,点B表示的数为4,阅读并解决相应问题.
(1)、若两人完成了2次移动游戏第一次甲、乙都错,第二次甲对乙错,此时甲、乙两人的距离为;(2)、从如图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对n次,则他最终停留的位置对应的数是什么?试用含n的代数式表示,并求该位置距离原点O最近时n的值;(3)、从如图的位置开始,若进行了k次移动游戏后,甲与乙的位置相距2个单位,直接写出k的值.25. 如图,数轴上点A表示的数为-3,点B表示的数为4,阅读并解决相应问题.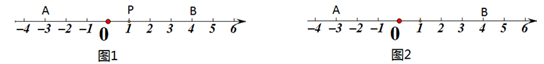 (1)、问题发现:若在数轴上存在一点P,使得点P到点A的距离与点P到点B的距离之和等于n,则称点P为点A、B的“n节点”.如图1,若点P表示的数为1,点P到点A的距离与点P到点B的距离之和为4+3=7,则称点P为点A、B的“7节点”.
(1)、问题发现:若在数轴上存在一点P,使得点P到点A的距离与点P到点B的距离之和等于n,则称点P为点A、B的“n节点”.如图1,若点P表示的数为1,点P到点A的距离与点P到点B的距离之和为4+3=7,则称点P为点A、B的“7节点”.填空:①若点P表示的数为-2,则n的值为;
②数轴上表示整数的点称为整点,若整点P为A、B的“7节点”,则这样的整点P共有个.
(2)、类比探究:如图2,若点P为数轴上一点,且点P到点A的距离为1,请你求出点P表示的数及n的值.(3)、拓展延伸:若点P在数轴上运动 不与点A、B重合 ,满足点P到点B的距离等于点P到点A的距离的 ,且此时点P为点A、B的“n的节点”,请写出点P表示的数及n的值.26. 如图,在数轴上点A表示的数是﹣3,点B在点A的右侧,且到点A的距离是18;点C在点A与点B之间,且到点B的距离是到点A距离的2倍.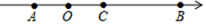 (1)、点B表示的数是;点C表示的数是;(2)、若点P从点A出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.
(1)、点B表示的数是;点C表示的数是;(2)、若点P从点A出发,沿数轴以每秒4个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.①当P运动到C点时,点Q所表示的数是多少?
②当t为何值时,P、Q之间的距离为6?
③若点P与点C之间的距离表示为PC,点Q与点B之间的距离表示为QB.在运动过程中,是否存在某一时刻使得PC + QB = 5?若存在,请求出此时点P表示的数;若不存在,请说明理由.
27. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示 ,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P、Q同时出发,点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问: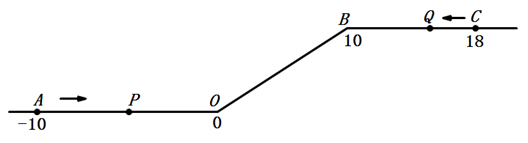 (1)、动点P从点A运动至C点需要多少时间?(2)、P、Q两点相遇时,求出相遇点M所对应的数是多少;(3)、求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.28. (阅读理解)
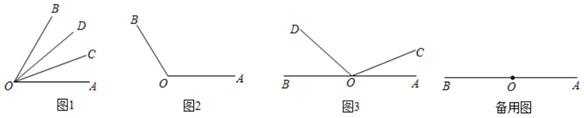
(1)、动点P从点A运动至C点需要多少时间?(2)、P、Q两点相遇时,求出相遇点M所对应的数是多少;(3)、求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.28. (阅读理解)射线 是 内部的一条射线,若 ,则我们称射线 是射线 的伴随线.如图1, , ,则 ,称射线 是射线 的伴随线;同时,由于 ,称射线 是射线 的伴随线.
 (1)、(知识运用)
(1)、(知识运用)如图2, ,射线 是射线 的伴随线,则 .若 的度数是 ,射线 是射线 的伴随线,则 的度数是.(用含 的代数式表示).
(2)、如图 , ,射线 与射线 重合,并绕点 以每秒 的速度逆时针旋转,射线 与射线 重合,并绕点 以每秒 的速度顺时针旋转,当射线 与射线 重合时,运动停止.①是否存在某个时刻 (秒),使得 的度数是 ,若存在,求出 的值,若不存在,请说明理由.
②当 为多少秒时,射线 、 、 中恰好有一条射线是其余两条射线中某一条射线的伴随线,请直接写出 的值.