2022年初中数学苏科版《中考二轮复习》专题一 数与式、方程与不等式 1.4 因式分解
试卷更新日期:2022-04-08 类型:二轮复习
一、单选题
-
1. 下列等式由左边至右边的变形中,属于因式分解的是( )A、x2+5x-1=x(x+5)-1 B、x2-4+3x=(x+2)(x-2)+3x C、x2-9=(x+3)(x-3) D、(x+2)(x-2)=x2-42. 已知 ,则 的值为( )A、0 B、1 C、3 D、43. 下列各式中,计算结果是x3+4x2-7x-28的是( )A、(x2+7)(x+4) B、(x2-2)(x+14) C、(x+4)(x2-7) D、(x+7)(x2-4)4. 2x3-x2-5x+k 中,有一个因式为(x-2),则 k 值为( )
A、2 B、6 C、-6 D、-25. 已知△ABC的三边a,b,c满足 ,则△ABC为( ).A、钝角三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形6. 若多项式因式分解后的一个因式是的值是( )A、-2 B、0 C、-1 D、17. 多项式x2y2-y2-x2+1因式分解的结果是( )A、(x2+1)(y2+1) B、(x-1)(x+1)(y2+1) C、(x2+1)(y+1)(y-1) D、(x+1)(x-1)(y+1)(y-1)8. 已知a= x+20,b= x+19,c= x+21,那么代数式a2+b2+c2﹣ab﹣bc﹣ac的值是( )
A、4 B、3 C、2 D、19. 若x3+x2+x+1=0,则x﹣27+x﹣26+…+x﹣1+1+x+…+x26+x27的值是( )A、1 B、0 C、﹣1 D、210. 任何一个正整数 都可以进行这样的分解: ( 、 是正整数,且 ),如果 在 的所有这种分解中两因数之差的绝对值最小,我们就称 是 的最佳分解,并规定: .例如18可以分解成 , , 这三种,这时就有 ,给出下列关于 的说法:① ;② ;③ ;④若 是一个完全平方数,则 ,其中正确说法的个数是( )
A、4 B、3 C、2 D、1二、填空题
-
11. 因式分解:x3-5x2+4x= .12. 因式分解:ax2-7ax+6a=13. 分解因式:(a+2)(a-2)-3a=14. 若
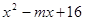 是完全平方式,那么 m =. 15. 若一个长方形的长、宽分别为 a、b,周长为 12,面积为 8,则 a2b+ab2=
是完全平方式,那么 m =. 15. 若一个长方形的长、宽分别为 a、b,周长为 12,面积为 8,则 a2b+ab2=
16. 已知a与b互为相反数,则代数式a2+2ab+b2-2018的值为 .17. 若一个正方形的面积为 4a2+12ab+9b2(a>0,b>0),则这个正方形的边长为 .
18. 数348-1 能被30以内的两位数(偶数)整除,这个数是三、解答题
-
19. 把下列多项式因式分解:(1)、ax2-16ay2;
(2)、a3+ab2-2a2b;
(3)、x2y(m-n)-xy2(n-m)
(4)、a2+2ab+b2-9a
20. 分解因式:(1)、6a2b﹣4a3b3﹣2ab(2)、25m2﹣n2(3)、4x2+12xy+9y2(4)、a2(x﹣y)﹣b2(x﹣y)(5)、﹣2a2x4+16a2x2﹣32a2(6)、(a2﹣a)2﹣(a﹣1)2 .21. 对于二次三项式x2+2ax+a2可以直接用公式法分解为(x+a)2的形式,但对于二次三项式x2+2ax﹣3a2 , 就不能直接用公式法了,我们可以在二次三项式x2+2ax﹣3a2中先加上一项a2 , 使其成为完全平方式,再减去a2这项,使整个式子的值不变.于是有x2+2ax﹣3a2=x2+2ax﹣3a2+a2﹣a2=x2+2ax+a2﹣a2﹣3a2=(x+a)2﹣(2a)2=(x+3a)(x﹣a).像上面这样把二次三项式分解因式的方法叫做添项法.
请用上述方法把m2﹣6m+8分解因式.
22. 常用的分解因式的方法有提取公因式法、公式法及十字相乘法,但有更多的多项式只用上述方法就无法分解,如x2-4y2-2x+4y,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了.过程为:x2-4y2-2x+4y=(x+2y)(x-2y)-2(x-2y)=(x-2y)(x+2y-2).这种分解因式的方法叫分组分解法.利用这种方法解决下列问题:
(1)、分解因式x2-2xy+y2-16;(2)、△ABC三边a,b,c 满足a2-ab-ac+bc=0,判断△ABC的形状.23. 请认真观察图形,解答下列问题: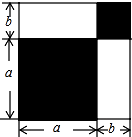 (1)、根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);(2)、由(1),你能得到怎样的等量关系?请用等式表示;(3)、如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4-b4的值.24. 如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)
(1)、根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);(2)、由(1),你能得到怎样的等量关系?请用等式表示;(3)、如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4-b4的值.24. 如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为m的大正方形,两块是边长都为n的小正方形,五块是长为m,宽为n的全等小矩形,且m>n.(以上长度单位:cm)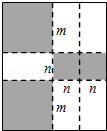 (1)、观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为;(2)、若每块小矩形的面积为10cm2 , 四个正方形的面积和为58cm2 , 试求图中所有裁剪线(虚线部分)长之和.25. 下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
(1)、观察图形,可以发现代数式2m2+5mn+2n2可以因式分解为;(2)、若每块小矩形的面积为10cm2 , 四个正方形的面积和为58cm2 , 试求图中所有裁剪线(虚线部分)长之和.25. 下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.解:设x2-4x=y,
则原式=(y+2)(y+6)+4(第一步)
=y2+8y+16(第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步).
(1)、该同学第二步到第三步运用了因式分解的( )
A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式(2)、该同学因式分解的结果是否彻底?(填“彻底”或“不彻底”).若不彻底,请直接写出因式分解的最后结果:(3)、请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.26. 阅读以下文字并解决问题:对于形如x2+2ax+a2这样的二次三项式,我们可以直接用公式法把它分解成(x+a)2的形式,但对于二次三项式x2+6x﹣27,就不能直接用公式法分解了.此时,我们可以在x2+6x﹣27中间先加上一项9,使它与x2+6x的和构成一个完全平方式,然后再减去9,则整个多项式的值不变. 即:x2+6x﹣27=(x2+6x+9)﹣9﹣27=(x+3)2﹣62=(x+3+6)(x+3﹣6)=(x+9)(x﹣3),像这样,把一个二次三项式变成含有完全平方式的形式的方法,叫做配方法.
(1)、利用“配方法”因式分解:x2+4xy﹣5y2
(2)、如果a2+2b2+c2﹣2ab﹣6b﹣4c+13=0,求a+b+c的值.
27. 阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)、已知x2﹣2xy+2y2+6y+9=0,求xy的值;(2)、已知△ABC的三边长a、b、c都是正整数,且满足a2+b2﹣10a﹣12b+61=0,求△ABC的最大边c的值;(3)、已知a﹣b=8,ab+c2﹣16c+80=0,求a+b+c的值.28. 我们知道某些代数恒等式可用一些卡片拼成的图形面积来解释,例如:图A可以用来解释a2+2ab+b2=(a+b)2 , 实际上利用一些卡片拼成的图形面积也可以对某些二次三项式进行因式分解.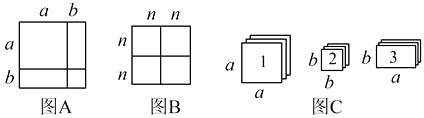 (1)、图B可以解释的代数恒等式是(2)、现有足够多的正方形和矩形卡片,如图C:
(1)、图B可以解释的代数恒等式是(2)、现有足够多的正方形和矩形卡片,如图C:①若要拼出一个面积为(a+2b)(a+b)的矩形,则需要1号卡片张,2号卡片张,3号卡片张;
②试画出一个用若干张1号卡片、2号卡片和3号卡片拼成的矩形,使该矩形的面积为2a2+5ab+2b2.