黑龙江省哈尔滨市第四十七中学2020--2021学年六年级下学期数学期中考试试卷（五四制）

试卷更新日期：2022-04-08 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共计30分）

1. -2的相反数是（）

A、2 B、-2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列各式中正确的是（）

A、 $2^{2} = {(- 2)}^{2}$ B、 $3^{3} = {(- 3)}^{3}$ C、 $- 2^{2} = | - 2^{2} |$ D、 $- 3^{3} = | 3^{3} |$

查看试题解析
3. 下列式子 $\frac{1}{4} x^{3} - y z$ ， $\frac{5}{x} + 3$ ，abc+6，0， $\frac{1}{m + n}$ ， $\frac{3 x}{π}$ 中，整式有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 下面四个几何体中，从左面看是四边形的几何体有（）个．

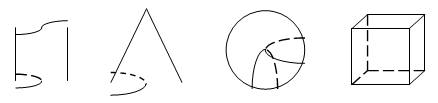A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列去括号中，正确的是（）

A、a－(2b－3c)＝a－2b－3c B、x³－(3x²＋2x－1)＝x³－3x²－2x－1 C、2y²＋(－2y＋1)＝2y²－2y＋1 D、－(2x－y)－(－x²＋y²)＝－2x＋y＋x²＋y²

查看试题解析
6. 下列说法正确的是（）

A、 ${\frac{2}{a^{3}}}^{} - a^{2} b^{2}$ 是四次二项式 B、 $a b - a^{2} b^{4} + 2$ 的最高次项是 $a^{2} b^{4}$ C、 $2 x^{2} - 3 x y - 1$ 是二次三项式 D、 $\frac{3 - x}{3}$ 的最高次项的系数是 $\frac{1}{3}$

查看试题解析
7. 下面四个整式中，不能表示图中阴影部分面积的是（）

A、 $x^{2} + 5 x$ B、 $3 (x + 2) + x^{2}$ C、 $x (x + 3) + 6$ D、 $(x + 3) (x + 2) - 2 x$

查看试题解析
8. 用四舍五入法按要求对0.15029分别取近似值，其中错误的是（）

A、0.150(精确到千分位) B、0.15(精确到百分位) C、0.1502(精确到0.0001) D、0.2(精确到0.1)

查看试题解析
9. 已知 $a$ 、 $b$ 为有理数，下列式子：① $| a b |$ ＞ $a b$ ；② $\frac{a}{b}$ ＜0；③ $| \frac{a}{b} | = - \frac{a}{b}$ ；④ $a^{3} + b^{3} = 0$
其中一定能够表示 $a$ 、 $b$ 异号的有（）个

A、1 B、2 C、3 D、4

查看试题解析
10. 下列语句正确的是（）
①绝对值最小的数是0；②平方等于它本身的数只有1；③任何有理数都有倒数；④绝对值不相等的两个数的和一定不为0；⑤两个数的和大于一个加数，而小于另一个加数，那么这两数一定是异号；⑥一个有理数不是整数就是分数；⑦单项式与多项式的和必为多项式。

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题：（每题3分，共计30分）

11. 科学防疫从勤洗手开始，一双没洗干净的手上带有各种细菌病毒大约850 000 000个，这个数据用科学记数法表示为.

查看试题解析
12. 如果一个数的 $\frac{3}{4}$ 等于 $- 1 \frac{3}{4}$ 平方的相反数，则这个数是.

查看试题解析
13. 用代数式表示“ 的3倍与的和”，结果是.

查看试题解析
14. 已知（m-3）xy^|m|+1 是关于x、y的五次单项式，则m的值是.

查看试题解析
15. 若 $| x - \frac{1}{2} | + {(y + 2)}^{2} = 0$ ，则 ${(x y)}^{2015}$ 的值为.

查看试题解析
16. 一个代数式加上 $- y^{2} + x^{2}$ 后等于 $x^{2} + y^{2}$ ，则这个代数式为.

查看试题解析
17. 当温度上升 1℃ 时，某种金属丝伸长 0.002mm，反之，当温度每下降 1℃ 时，金属丝缩短 0.002mm.把 15℃的这种金属丝加热到 50℃，再使它冷却降温到 5℃，最后的长度比原长度伸长mm.

查看试题解析
18. 某轮船顺水航行3h，逆水航行1.5h，已知轮船在静水中的速度是akm/h，水流速度是ykm/h，该轮船顺水航行比逆水航行多航行了千米.

查看试题解析
19. 已知数轴上A、B两点对应的数分别为-10、20，P为数轴上一动点，对应的数为x，若P点到A、B距离的比为3：2，则点P表示的数为.

查看试题解析
20. 如图是一个正面标有A的正方体，及它的展开图，已知A的对面是一个三次单项式，正方体的左面与右面标注的单项式是同类项.则代数式： $a^{b} + m$ 的值为.

查看试题解析

三、解答题：（21题12分，22题～23题6分，24题～25题8分，26题～27题10分，共计60分）

21. 计算：

(1)、 $- 4 - （ + 6 ） - (- 10) + (- 8)$

(2)、 $1 \div (\frac{1}{6} - \frac{1}{3}) \times 0.5$

(3)、7× $\frac{3}{4}$ $- (- 7)$ × $\frac{1}{2}$ ＋7× $(- \frac{1}{4})$

(4)、－1⁴－ $\frac{1}{6}$ ×[3－(－3)²]

查看试题解析
22. 化简：

(1)、 $3 x^{2} - 1 + 2 x - 5 - 3 x - x^{2}$

(2)、 $\frac{1}{3} (a b^{2} + 3 a^{2} b) - \frac{5}{2} (b a^{2} - 7 a b^{2})$

查看试题解析
23. 先化简，再求值：
$4 x y - 2 (x^{2} + \frac{5}{2} x y - y^{2}) + 2 (x^{2} + 3 x y + 1) - 3$ ，其中 $x = - 2$ ， $y = \frac{1}{2}$ .

查看试题解析
24. 某汽车厂计划每天平均生产200辆汽车，由于工人实行轮休，每日上班人数不一定相等，实际每日生产量与计划量相比有出入。下表记录了某周五个工作日每天实际生产情况（超过计划产量记为正数，少于计划产量记为负数）：

星期

一

二

三

四

五

增减

+6

-1

－5

+7

-3

(1)、计算本周前三天共生产了多少辆汽车？

(2)、该厂实行每日计件工资制，每生产一辆车可得150元，若超额完成任务，则超过部分每辆另奖30元，少生产一辆扣25元，那么该工厂这周五天的工资总额是多少元？

(3)、若将上面第（2）问中“实行每日计件工资制”改为“实行每周计件工资制”，其他条件不变，在此方式下这一周工人的工资总额与按日计件的工资总额哪一个更多？请通过计算说明理由。

查看试题解析
25. 根据规律填空，然后你能很快算出 $1995^{2}$ 吗？

(1)、通过计算，探究规律：
15²=225可写成 $100 \times 1 \times (1 + 1) + 25$ ，25²=625可写成 $100 \times 2 \times (2 + 1) + 25$ ，

35²=1225可写成 $100 \times 3 \times (3 + 1) + 25$ ，45²=2025可写成 $100 \times 4 \times (4 + 1) + 25$ ，

75²=5625可写成， 85²=7225可写成.

(2)、从第（1）题的结果，归纳、猜想：（100n+5）²= .（用含有n的式子表示）

(3)、根据上面的归纳、猜想，请算出： $1995^{2}$ = .

查看试题解析

26. 如图，一扇窗户，窗框为铝合金材料，下面是由两个大小相等的长方形窗框构成，上面是由三个大小相等的扇形组成的半圆窗框构成，窗户半圆部分安装彩色玻璃，两个长方形部分安装透明玻璃(本题中π取 3，长度单位为米).

(1)、一扇这样窗户一共需要铝合金多少米?(用含 x，y 的代数式表示)

(2)、一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含 x，y 的代数式表示)

(3)、某公司需要购进 20 扇窗户，在同等质量的前提下，甲、乙两个厂商分别给出如下报价：

铝合金(米/元)

彩色玻璃(平方米/元)

透明玻璃(平方米/元)

甲厂商

200

不超过100平方米的部分，90元/平方米，

超过100平方米的部分，70元/平方米

乙厂商

220

80元/平方米，每购1平方米透明玻璃送0.1米铝合金

当 x=2，y=3 时，该公司在哪家厂商购买窗户合算?

查看试题解析

27. 单项式 $- 60 x^{25} y^{5}$ 的系数为a，次数为b。如图，点O为原点，A、B在数轴上表示的数分别为a、b。

(1)、直接写出A点表示的数为， B点表示的数为。

(2)、现有两个动点P、Q均从点A出发，沿数轴正方向运动，点P的速度为每秒6个单位长度，点Q的速度为每秒3个单位长度。若点P出发两秒后点Q出发，当点P到达点B时，P、Q两点同时停止运动。设点P运动时间为t秒，运动过程中点P表示的数为x，点Q表示的数为y。求t为何值时， $| y | = 2 | x |$ 。

(3)、若动点P从点A出发沿数轴正方向运动，点P的速度为每秒5个单位长度，同时另一个动点N从B出发沿数轴负方向运动5秒后，再以每秒15个单位长度的速度继续匀速运动，N点运动过程中到达点A后调转方向返回。当点P到达点B时，两点都停止运动。若整个运动过程中，运动时间为7秒时，P、N两点相距20个单位长度，求点N最开始的速度。

查看试题解析

星期	一	二	三	四	五
增减	+6	-1	－5	+7	-3