山东省威海市文登区2020-2021学年六年级下学期期中考试数学试题
试卷更新日期:2022-04-08 类型:期中考试
一、单选题(每题3分,共36分)
-
1. 下列图形中,∠1与∠2不是同位角( )A、
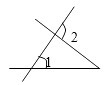 B、
B、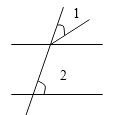 C、
C、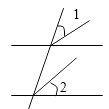 D、
D、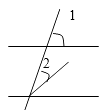
-
2. 2020年1月24日,中国疾控中心成功分离我国首株新型冠状病毒毒种,该毒种直径大约为80纳米(1纳米=0.000001毫米),数据“80纳米”用科学记数法表示为( )A、毫米 B、毫米 C、毫米 D、毫米
-
3. 图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;⑤线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.
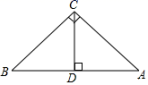 A、①④③⑥ B、①④⑥ C、②③ D、①④
A、①④③⑥ B、①④⑥ C、②③ D、①④ -
4. 下列图形中,由∠1=∠2能得到AB∥CD的是( )A、
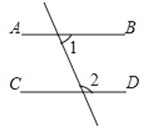 B、
B、 C、
C、 D、
D、
-
5. 如果用平方差公式计算 , 则可将原式变形为( )A、 B、 C、 D、
-
6. 与的关系是( )A、相等 B、互为相反数 C、前式是后式的倍 D、以上结论都不对
-
7. 一个多边形对角线的条数是边数的3倍,则这个多边形是( )A、七边形 B、八边形 C、九边形 D、十边形
-
8. 下列各图形中均有直线 ,则能使结论 成立的是( )A、
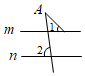 B、
B、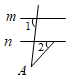 C、
C、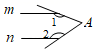 D、
D、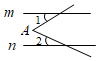
-
9. 在下列各式:①a-b=b-a ;②(a-b)2=(b-a)2 ;③(a-b)2=-(b-a)2 ;④(a-b)3=(b-a)3;⑤(a+b)(a-b)=(-a-b)(-a+b) 中,正确的有( )A、1个 B、2个 C、3个 D、4个
-
10. 若 , , 则( )A、2021 B、-2020 C、-2021 D、-2022
-
11. 下列计算错误的是( )A、 B、 C、 D、
-
12. 如图, , C点在EF上, , BC平分 , 且 . 下列结论:①AC平分;②;③;④ . 其中结论正确的个数有( )
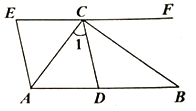 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个
二、填空题(每题3分,共18分)
-
13. , 则
-
14. 已知A,B两点之间的距离是5 cm,C是线段AB上的任意一点,则AC中点与BC中点间距离是 cm.
-
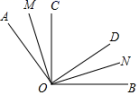
15. 如图OC、OD是∠AOB内部两条射线,OM平分∠AOC,ON平分∠DOB,若∠AOB=110°,∠MON= 70°,则∠COD =度
-
16. 一个角的补角加上 后,等于这个角的余角的 倍,则这个角是.
-
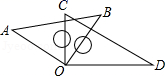
17. 将一幅三角板的两个直角顶点重合摆放,如图,若∠BOC= , 则∠AOD= .
-
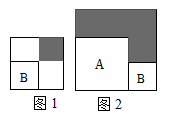
18. 有两个正方形A和B,现将B放在A的内部如图1所示,将A,B并列放置后构造新的正方形如图2所示,图1和图2的阴影部分面积分别为4和20,则正方形A,B的面积和为 .
三、解答题
-
19. 计算:(1)、﹣1-4+20190÷(﹣2)﹣2+(﹣)﹣2;(2)、(3ab3﹣a2b+ab)÷(﹣ab);(3)、2019×2021-20202+1(4)、先化简,再求值:(2a﹣b)2+(a+1﹣b)(a+1+b)﹣(a+1)2 , 其中a= , b=﹣2.
-
20. 利用网格画图,每个小正方形边长均为1
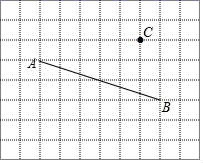 (1)、过点C画AB的平行线CD;
(1)、过点C画AB的平行线CD;
仅用直尺,过点C画AB的垂线,垂足为E;(2)、连接CA、CB,在线段CA、CB、CE中,线段最短,理由 .(3)、直接写出△ABC的面积为 . -
21. 已知满足.(1)、求的值;(2)、先化简,再求值:.
-
22. 如图,在四边形ABCD中,AB//CD, E为BC延长线上一点,AE交CD于点F,∠1=∠2,∠3=∠4,试说明AD//BE.
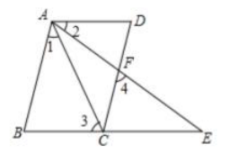
证明:∵ ∠3=∠4 ( )
且∠4 = ∠AFD ( )
∴∠3=∠AFD
在△ABC中,∠1+∠B+∠3= 180°
在△ADF中, = 180°
∵∠1=∠2,∠3=∠AFD
∴∠B=∠D ( )
∵AB//CD
∴∠B=∠DCE ( )
∴ (等量代换)
∴AD//BE ( )
-
23. 如图,在△ABC中,点D在边BC上,点G在边AB上,点E、F在边AC上,∠AGF=∠ABC =70° ,∠1+∠2=180° .
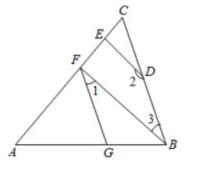 (1)、试判断BF与DE的位置关系,并说明理由:(2)、若DE⊥AC,∠2=150°,求∠AFG的度数.
(1)、试判断BF与DE的位置关系,并说明理由:(2)、若DE⊥AC,∠2=150°,求∠AFG的度数. -
24. 如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.
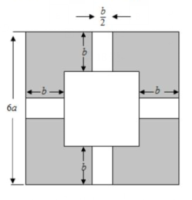 (1)、用含a、b的代数式表示草坪(阴影)面积并化简.(2)、若a=10, b=5, 计算草坪的造价.
(1)、用含a、b的代数式表示草坪(阴影)面积并化简.(2)、若a=10, b=5, 计算草坪的造价. -
25.
将一副三角板按如图方式摆放,两个直角顶点重合,∠A=60°,∠E=∠B=45°
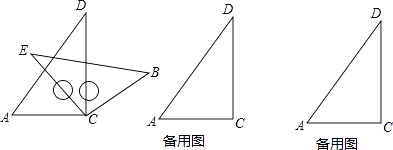 (1)、求证:∠ACE=∠BCD;(2)、猜想∠ACB与∠ECD数量关系并说明理由;(3)、按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
(1)、求证:∠ACE=∠BCD;(2)、猜想∠ACB与∠ECD数量关系并说明理由;(3)、按住三角板ACD不动,绕点C旋转三角板ECB,探究当∠ACB等于多少度时,AD∥CB.请在备用图中画出示意图并简要说明理由.
