2022年北师大数学七下期中复习阶梯训练：相交线与平行线（提高训练）
试卷更新日期：2022-04-08 类型：复习试卷
一、单选题
-
1. 如图，直线 ， 与直线 ， 相交，已知 ， ，则 的度数是（ ）
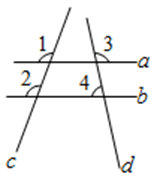A、 B、 C、 D、2. 如图所示，若 ， ， ，则 的度数是（ ）
A、70° B、60° C、50° D、40°3. 如图，直线AB、CD相交于点O，OE平分∠BOC，若∠BOD：∠BOE=1：2，则∠AOE的大小为（ ）
A、72° B、98° C、100° D、108°4. 已知∠1＝38°36′，∠2＝38.36°，∠3＝38.6°， 则下列说法正确的是（ ）A、∠1＝∠2 B、∠2＝∠3 C、∠1＝∠3 D、∠1、∠2、∠3互不相等5. 已知∠α是锐角，∠α与∠β互补，∠α与∠γ互余，则∠β-∠γ的值等于（ ）A、45° B、60° C、90° D、180°6. 若一个角比它的余角大30°，则这个角等于（ ）A、30° B、60° C、105° D、120°7. 如图，点A，O，B在一条直线上，OE⊥AB于点O，如果∠1与∠2互余，那么图中相等的角有（ ）
A、6对 B、5对 C、4对 D、3对8. 下列说法中，正确的是（ ）A、一个锐角的补角大于这个角的余角 B、一对互补的角中，一定有一个角是锐角 C、锐角的余角一定是钝角 D、锐角的补角一定是锐角9. 在灯塔O处观测到轮船A位于灯塔北偏西54°的方向，同时观测到轮船B位于灯塔南偏东15°的方向，那么∠AOB的大小为（ ）
A、131° B、141° C、151° D、159°10. 如图，点O在直线上， ， 则的大小为（ ）
A、 B、 C、 D、二、填空题
-
11. 如图，点 O 在直线 AB 上，过点 O 作射线 OC，若∠AOC=53°17′28″，则∠BOC 的度数是 ．
12. 一个角的补角比它的余角的4倍少60°，这个角的度数为 ．13. 如图，码头、火车站分别位于A，B两点，直线a和b分别表示铁路与河流.
①两点确定一条直线；②两点之间线段最短；③垂线段最短．(1)、从码头A到火车站B怎样走最近，请画图，并选择理由 （填序号）．(2)、从码头A到铁路a怎样走最近，请画图，并选择理由 （填序号）．14. 已知一个角的余角是35°，那么这个角的度数是。15. 如图， 直线 与直线 相交于点 ， 已知 ，则 .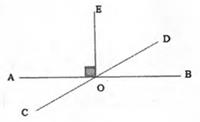
16. 一个角为 ， 则它的余角度数为 ．三、解答题
-
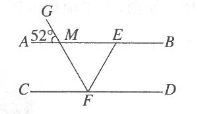
17. 如图，已知 平分 交AB于点 ，求 的度数.
18. 如图，点A、O、B在同一条直线上，射线OD平分∠AOC，且∠DOE＝90°．求证：OE平分∠BOC．
19. 如果一个角的补角是这个角的余角的4倍，求这个角.20. 如图，点 在BC的延长线上， ， .求证： .
21. 如图：已知O是直线CD上的点，OA平分∠BOC，∠AOC＝40°，求∠BOD度数.
22. 根据解答过程填空（写出推理理由或数学式）：如图，已知∠DAF＝∠F，∠B＝∠D，试说明AB∥DC．
证明：∵∠DAF＝∠F（已知）．
∴AD∥BF（ ▲ ），
∴∠D＝∠DCF（ ▲ ）．
∵∠B＝∠D（已知），
∴（ ▲ ）＝∠DCF（等量代换），
∴AB∥DC（ ▲ ）．
四、综合题
