2022年北师大数学七下期中复习阶梯训练：整式的乘除（优生加练）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 在矩形ABCD内，将两张边长分别为a和b（ $a > b$ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $S_{1}$ ，图2中阴影部分的面积为 $S_{2}$ .当 $A D - A B = 3$ 时， $S_{2} - S_{1}$ 的值是（）

A、 $3 a$ B、 $3 b$ C、 $3 a - 3 b$ D、 $- 3 a$

查看试题解析
2. 记 $n = (1 + 3) (1 + 3^{2}) (1 + 3^{4}) \dots (1 + 3^{256})$ ，则 $2 n + 1$ （）

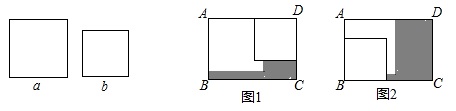A、一个偶数 B、一个质数 C、一个整数的平方 D、一个整数的立方

查看试题解析
3. 已知 $a_{1}$ ， $a_{2}$ ，…， $a_{2020}$ 都是正数，如果 M＝（ $a_{1}$ + $a_{2}$ +…+ $a_{2019}$ ）（ $a_{2}$ + $a_{3}$ +…+ $a_{2020}$ ），N＝（ $a_{1}$ + $a_{2}$ +…+ $a_{2020}$ ）（ $a_{2}$ + $a_{3}$ +…+ $a_{2019}$ ），那么 M，N 的大小关系是（）

A、M＞N B、M＝N C、M＜N D、不确定

查看试题解析
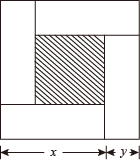4. 如图，大正方形的边长为 $m$ ，小正方形的边长为 $n$ ， $x$ ， $y$ 表示四个相同长方形的两边长（ $x > y$ ）.则① $x - y = n$ ；② $x y = \frac{m^{2} - n^{2}}{4}$ ；③ $x^{2} - y^{2} = m n$ ；④ $x^{2} + y^{2} = \frac{m^{2} - n^{2}}{2}$ ，中正确的是（）

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析
5. 我国宋朝数学家杨辉1261年的著作《详解九章算法》给出了在 ${(a + b)}^{n} (n$ 为非负整数）的展开式中，把各项系数按一定的规律排成右表（展开后每一项按 $a$ 的次数由大到小的顺序排列）．人们把这个表叫做“杨辉三角”．据此规律，则 ${(x + 1)}^{2019}$ 展开式中含 $x^{2018}$ 项的系数是 $($ 　　 $)$

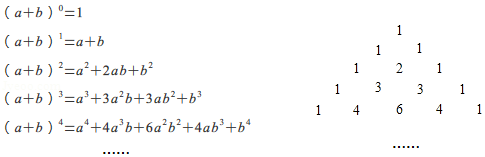A、2016 B、2017 C、2018 D、2019

查看试题解析
6. 在求 $1 + 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9}$ 的值时，小林发现：从第二个加数起每一个加数都是前一个加数的6倍，于是她设： $S = 1 + 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9}$ ……①
然后在①式的两边都乘以6，得： $6 S = 6 + 6^{2} + 6^{3} + 6^{4} + 6^{5} + 6^{6} + 6^{7} + 6^{8} + 6^{9} + 6^{10}$ ……②

②-①得 $6 S - S = 6^{10} - 1$ ，即 $5 S = 6^{10} - 1$ ，所以 $S = \frac{6^{10} - 1}{5}$ .

得出答案后，爱动脑筋的小林想：如果把“6”换成字母“a”(a≠0且a≠1)，能否求出 $1 + a + a^{2} + a^{3} + a^{4} + ... + a^{2018}$ 的值?你的答案是（）

A、 $\frac{a^{2018} - 1}{a - 1}$ B、 $\frac{a^{2019} - 1}{a - 1}$ C、 $\frac{a^{2018} - 1}{a}$ D、 $a^{2019} - 1$

查看试题解析
7. 若A＝(2＋1)(2²＋1)(2⁴＋1)(2⁸＋1)＋1，则A的末位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
8. 已知a，b，c为非零的实数，则 $\frac{a}{| a |} + \frac{a b}{| a b |} + \frac{a c}{| a c |} + \frac{b c}{| b c |}$ 的可能值的个数为（）

A、4 B、5 C、6 D、7

查看试题解析
9. 不论x、y为什么实数，代数式x²+y²+2x﹣4y+7的值（）

A、总不小于2 B、总不小于7 C、可为任何实数 D、可能为负数

查看试题解析
10. 方程（x²+x﹣1）^x⁺³=1的所有整数解的个数是（）

A、5个 B、4个 C、3个 D、2个

查看试题解析

二、填空题

11. 数学活动课上，小明同学尝试将正方形纸片剪去一个小正方形，剩余部分沿虚线剪开，拼成新的图形。现给出下列3种不同的剪、拼方案，其中能够验证平方差公式的方案是。(请填上正确的序号)

查看试题解析
12. 已知下列等式：；① $1^{3} = 1^{2}$ ；② $1^{3} + 2^{3} = 3^{2}$ ；③ $1^{3} + 2^{3} + 3^{3} = 6^{2}$ ；④ $1^{3} + 2^{3} + 3^{3} + 4^{3} = 10^{2}$ ……由此规律，则 $21^{3} + 22^{3} + 23^{3} + \dots + 50^{3} =$ ．

查看试题解析
13. 我国宋朝数学家杨辉在他的著作 $《$ 解：九章算法 $》$ 中提出“杨辉三角” $($ 如图 $)$ ，此图揭示了 ${(a + b)}^{n} (n$ 为非负整数 $)$ 展开式的项数及各项系数的有关规律.
例如： ${(a + b)}^{0} = 1$ ，它只有一项，系数为1；系数和为1；

${(a + b)}^{1} = a + b$ ，它有两项，系数分别为1，1，系数和为2；

${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ ，它有三项，系数分别为1，2，1，系数和为4；

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 {ab}^{2} + b^{3}$ ，它有四项，系数分别为1，3，3，1，系数和为8； $\dots$ ，

则 ${(a + b)}^{n}$ 的展开式共有项，系数和为.

查看试题解析
14. 观察、归纳：
（x﹣1）（x+1）＝x²﹣1；

（x﹣1）（x²+x+1）＝x³﹣1；

（x﹣1）（x³+x²+x+1）＝x⁴﹣1；

…

请你根据以上等式的规律，完成下列问题：

⑴（x﹣1）（xⁿ+…+x²+x+1）＝﹣1；

⑵计算：1+2+2²+…+2²⁰¹⁹＝．

查看试题解析
15. 如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）．

①图2中的阴影部分的面积为；

②观察图2请你写出（a+b）²、（a﹣b）²、ab之间的等量关系是；

③根据（2）中的结论，若x+y=5，x•y= $\frac{9}{4}$ ，则（x﹣y）²=；

④实际上通过计算图形的面积可以探求相应的等式．

如图3，你发现的等式是．

查看试题解析
16. 已知a₁= $1 - \frac{1}{2^{2}}$ ，a₂= $1 - \frac{1}{3^{2}}$ ，a₃= $1 - \frac{1}{4^{2}}$ ，…，a_n= $1 - \frac{1}{{(n + 1)}^{2}}$ ，S_n=a₁•a₂…a_n ，则S₂₀₁₅=.

查看试题解析

三、解答题

17. 小张和小李玩猜数游戏，小张说：“你随便选三个一位数按这样的步骤去运算，①把第一个数乘5；②再加上10；③把所得结果乘以2；④加上第二个数；⑤把所得结果乘以10；⑥加上第三个数；只要你告诉我最后的得数，我就能知道你所想的三个一位数．”小李按照以上步骤试了几次，过程如下：

小李选定了1，2，3
小张选定了5，6，7
①
$1 \times 5 = 5$
$5 \times 5 = 25$
②
$5 + 10 = 15$
$25 + 10 = 35$
③
$15 \times 2 = 30$
$35 \times 2 = 70$
④
$30 + 2 = 32$
$70 + 7 = 77$
⑤
$32 \times 10 = 320$
$77 × 10 = 770$
⑥
$320 + 3 = 323$
$770 + 6 = 776$
小张介绍了他的计算奥秘：将最后的得数减去200，所得的结果百位数就是第一个数，十位数就是第二个数，个位数就是第三个数．
探究一：证明小张想法的符合题意性

小李选定了 $a$ ， $b$ ， $c$
①
$5 a$
②
$5 a + 10$
③
$(5 a + 10) × 2 = 10 a + 20$
④
$10 a + 20 + b$
⑤
$(10 a + 20 + b) \times 10 = 100 a + 10 b + 200$
⑥
$100 a + 10 b + c + 200$
小张将最后的得数减去200：
$100 a + 10 b + c + 200 - 200 = 100 a + 10 b + c$ ，
所以结果百位数就是第一个数，十位数就是第二个数，个位数就是第三个数．小李听完后深受启发也设计了自己的运算程序，让小张随便选三个一位数按这样的步骤去运算：
①把第一个数乘5，再加上5；
②把第二个数乘20，再加上2；
③将①的运算结果与②的运算结果相乘，再加上第三个数；
④减去第一个数与第二个数乘积的100倍．
小李说：“只要小张告诉我最后的得数，我就能知道小张一开始所想的三个一位数。”
小李是如何知道的呢？请你模仿探究一的证明过程填写下表：
探究二：证明小李想法的符合题意性

设小张选定的三个数为 $x$ ， $y$ ， $z$
①
②
③
④
请介绍小李的计算奥秘，描述：你是怎样由最后的得数，识别出最初选定的三个一位数的？

查看试题解析
18. 证明：在a+b+c=0时，a³+b³+c³=3abc．

查看试题解析
19. 如图，正方形 $A B C D$ 和 $C E F G$ 的边长分别为 $m$ 、 $n$ ，试用 $m$ 、 $n$ 的代数式表示三角形 $B D F$ 的面积 $S$ ．

查看试题解析
20. 教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：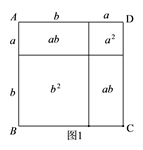

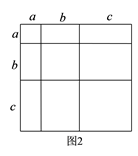
（1）把它看成是一个大正方形，则它的面积为 ${(a + b)}^{2}$ ；
（2）把它看成是2个小长方形和2个小正方形组成的，则它的面积为 $a^{2} + 2 a b + b^{2}$ ；因此，可得到等式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ .
① 类比教材中的方法，由图2中的大正方形可得等式：                          .
② 试在图2右边空白处画出面积为 $2 a^{2} + 3 a b + b^{2}$ 的长方形的示意图（标注好a、b），由图形可知，多项式 $2 a^{2} + 3 a b + b^{2}$ 可分解因式为：                          ．
在上方空白处画出②中的示意图
③ 若将代数式 ${(a_{1} + a_{2} + a_{3} + \dots + a_{20})}^{2}$ 展开后合并同类项，得到多项式N，则多项式N的项数一共有                          项.

查看试题解析
21. 解答发现：
（1）当a＝3，b＝2时，分别求代数式（a＋b）²和a²＋2ab＋b²的值，并观察这两个代数式的值有什么关系？
（2）再多找几组你喜欢的数试一试，从中你发现了什么规律？
（3）利用你所发现的规律计算a＝1. 625，b＝0. 375时，a²＋2ab＋b²的值？

查看试题解析
22. 5a－{－3b＋[6c－2a－(a－c)]}－[9a－(7b＋c)]

查看试题解析

四、综合题

23. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例.如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了 ${(a + b)}^{n} (n$ 为正整数)的展开式(按 $a$ 的次数由大到小的顺序排列)的系数规律.例如，在三角形中第三行的三个数1，2，1，恰好对应 ${(a + b)}^{2} = a^{2} +$ $2 a b + b^{2}$ 展开式中的系数；第四行的四个数1，3，3，1，恰好对应 ${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ 展开式中的系数.

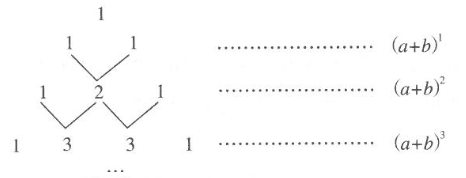(1)、根据上面的规律，写出 ${(a + b)}^{5}$ 的展开式；

(2)、利用上面的规律计算： $2^{5} - 5 \times 2^{4} + 10 \times 2^{3} - 10 \times 2^{2} + 5 \times 2 - 1$ .

查看试题解析
24. 观察下列算式。
（x-2）（x-3）=x²-5x+6；
（x+5）（x-2）=x²+3x-10；
（x+3）（x+6）=x²+9x+18；
（x+9）（x-10）=x²-x-90；
……

(1)、如上面算式中的两个一次二项式相乘，结果是一个次项式；其中一次项的系数和常数项分别和原来的两个二项式的常数项具有怎样的关系？

从上面的计算中总结规律，写出下式的结果：

（x+a）（x+b）=.

(2)、请利用你的结论直接写出下列两个二项式相乘的结果：
（x+5）（x-1）=

（x+11）（x-30）=.

查看试题解析
25. 7张如图1的长为a，宽为b（a＞b）的小长方形纸片，按如图2、3的方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．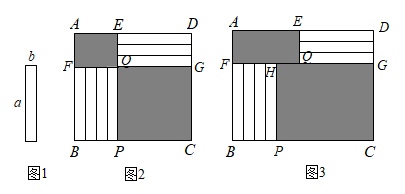

(1)、如图2，点E、Q、P在同一直线上，点F、Q、G在同一直线上，右下角与左上角的阴影部分的面积的差为（用含a、b的代数式表示），矩形ABCD的面积为（用含a、b的代数式表示）；

(2)、如图3，点F、H、Q、G在同一直线上，设右下角与左上角的阴影部分的面积的差为S，PC＝x．当BC的长度变化时，按照同样的放置方式，S始终保持不变，那么a、b必须满足什么条件？

查看试题解析

	小李选定了1，2，3	小张选定了5，6，7
①	$1 \times 5 = 5$	$5 \times 5 = 25$
②	$5 + 10 = 15$	$25 + 10 = 35$
③	$15 \times 2 = 30$	$35 \times 2 = 70$
④	$30 + 2 = 32$	$70 + 7 = 77$
⑤	$32 \times 10 = 320$	$77 × 10 = 770$
⑥	$320 + 3 = 323$	$770 + 6 = 776$

	小李选定了 $a$ ， $b$ ， $c$
①	$5 a$
②	$5 a + 10$
③	$(5 a + 10) × 2 = 10 a + 20$
④	$10 a + 20 + b$
⑤	$(10 a + 20 + b) \times 10 = 100 a + 10 b + 200$
⑥	$100 a + 10 b + c + 200$

	设小张选定的三个数为 $x$ ， $y$ ， $z$
①
②
③
④