天津市河西区2020-2021学年高二下学期数学期中考试试卷

试卷更新日期：2022-04-08 类型：期中考试

进入出卷网下载

一、单选题

1. 完成一件事有两类不同方案，在第1类方案中有 $m$ 种不同的方法，在第2类方案中有 $n$ 种不同的方法，那么完成这件事共有 $N$ 种不同的方法，其中 $N =$ （）

A、 $m + n$ B、 $m^{n}$ C、 $n^{m}$ D、 $m \times n$

查看试题解析
2. 若某射手每次射击击中目标的概率为0.9，每次射击的结果相互独立，则在他连续4次射击中，恰好有一次未击中目标的概率为（）

A、 $0.1 \times 0 . 9^{3}$ B、 $C_{4}^{1} \times 0 . 1^{3} \times 0.9$ C、 $0 . 1^{3} \times 0.9$ D、 $C_{4}^{1} \times 0.1 \times 0 . 9^{3}$

查看试题解析
3. 观察下列散点图，其中两个变量的相关关系判断正确的是（）

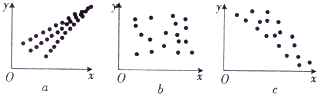A、a为正相关，b为负相关，c为不相关 B、a为负相关，b为不相关，c为正相关 C、a为负相关，b为正相关，c为不相关 D、a为正相关，b为不相关，c为负相关

查看试题解析
4. 如表是 $2 \times 2$ 列联表，则表中的 $a$ ､ $b$ 的值分别为（）

$y_{1}$
$y$
合计
$x_{1}$
$a$
8
35
$x$
11
34
45
合计
$b$
42
80

A、27､38 B、28､38 C、27､37 D、28､37

查看试题解析
5. 在 ${(x - \frac{2}{\sqrt{x}})}^{6}$ 的展开式中.常数项为（）

A、256 B、240 C、192 D、160

查看试题解析
6. 设随机变量 $X ∼ N (2 ， σ^{2})$ ， $P (0 < X < 4) = 0.3$ ，则 $P (X < 0) =$ （）

A、0.65 B、0.7 C、0.35 D、0.25

查看试题解析
7. 已知随机变量的分布列如表：
$X$
0
1
2
$P$
0.2
$a$
$b$
若 $E (X) = 1$ ，则 $D (X) =$ （）

A、0.1 B、0.2 C、0.4 D、0.6

查看试题解析
8. 学校要求学生从物理､历史､化学､生物､政治､地理这6科中选3科参加考试，规定先从物理和历史中任选1科，然后从其他4科中任选2科，不同的选法种数为（）

A、5 B、12 C、20 D、120

查看试题解析
9. 已知甲､乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 $\frac{2}{3}$ ，乙在每局中获胜的概率为 $\frac{1}{3}$ ，且各局胜负相互独立，则比赛停止时已打局数 $ξ$ 的均值为（）

A、 $\frac{17}{2}$ B、 $\frac{266}{81}$ C、 $\frac{274}{81}$ D、 $\frac{670}{81}$

查看试题解析

二、填空题

10. $A_{5}^{3} - C_{8}^{3} =$ .

查看试题解析
11. 已知变量 $x$ ， $y$ 之间具有线性相关关系，根据10对样本数据求得经验回归方程为 $\hat{y} = \hat{b} x - 3$ ，若 $\sum_{i = 1}^{10} x_{i} = 17$ ， $\sum_{i = 1}^{10} y_{i} = 4$ ，则 $\hat{b} =$ .

查看试题解析
12. 已知离散型随机变量 $X$ 的方差为1，则 $D (2 X + 1) =$ .

查看试题解析
13. 某班一天上午有4节课，下午有2节课，现要安排该班一天中语文、数学、政治、英语、体育、艺术6堂课的课程表，要求数学课排在上午，体育课排在下午，不同排法种数是；

查看试题解析
14. 假设有两箱零件，第一箱内装有10件，其中有2件次品；第二箱内装有20件，其中有3件次品.现从两箱中随意挑选一箱，然后从该箱中随机取1个零件，则取出的零件是次品的概率是.

查看试题解析
15. 现用5种颜色，给图中的5个区域涂色，要求相邻的区域不能涂同一种颜色，则不同的涂色方法共有.

查看试题解析

三、解答题

16. 若 ${(2 x + \sqrt{3})}^{4} = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + a_{4} x^{4}$ .

(1)、求 $a_{1} + a_{2} + a_{3} + a_{4}$ 的值；

(2)、求 ${(a_{0} + a_{2} + a_{4})}^{2} - {(a_{1} + a_{3})}^{2}$ 的值.

查看试题解析
17. 在5道试题中有3道代数题和2道几何题，每次从中随机抽出1道题，抽出的题不再放回.求：

(1)、第1次抽到代数题且第2次抽到几何题的概率；

(2)、在第1次抽到代数题的条件下，第2次抽到几何题的概率.

查看试题解析
18. 甲、乙两人参加某种选拔测试.规定每人必须从备选的6道题中随机抽出3道题进行测试,在备选的6道题中,甲答对其中每道题的概率都是 $\frac{3}{5}$ ,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.

(1)、求乙得分的分布列和数学期望;

(2)、规定:每个人至少得20分才能通过测试,求甲、乙两人中至少有一人通过测试的概率.

查看试题解析

	$y_{1}$	$y$	合计
$x_{1}$	$a$	8	35
$x$	11	34	45
合计	$b$	42	80

$X$	0	1	2
$P$	0.2	$a$	$b$