2022年北师大数学七下期中复习阶梯训练：整式的乘除（提高训练）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 某天数学课上，老师讲了单项式乘多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：- $3 x y (4 y - 2 x -$ $1) = - 12 x y^{2} + 6 x^{2} y + □ ， □$ 的地方被钢笔水弄污了，你认为 $□$ 内应填写（）

A、3xy B、 $- 3 x y$ C、-1 D、1

查看试题解析
2. 已知 $(- x) (2 x^{2} - a x - 1) - 2 x^{3} + 3 x^{2}$ 中不含 $x$ 的二次项，则 $a$ 的值是（）

A、3 B、2 C、-3 D、-2

查看试题解析
3. 有若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为35；其中5个如图⒉摆放，构造出一个长方形，其中阴影部分面积为102(各个小长方形之间不重叠不留空，则每个小长方形的面积为（）

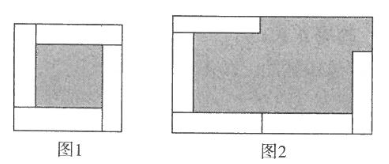A、4 B、8 C、12 D、16

查看试题解析
4. 有下列计算：
① $(6 a b + 5 a) \div a = 6 b + 5$ ；② $(8 x^{2} y - 4 x y^{2}) \div (- 4 x y) = - 2 x - y$ ；③ $(15 x^{2} y z - 10 x y^{2}) \div (5 x y) = 3 x - 2 y$ ；④ $(5 m^{2} + 15 m^{3} n - 20 m^{4}) \div (- 5 m^{2}) = 4 m^{2} - 3 m n - 1$ ；⑤ $(3 x^{2} y - 3 x y^{2} + x) \div x = 3 x y - 3 y^{2}$ .

其中不正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若 $3 y - 2 x + 2 = 0$ ，则 $9^{x} \div 27^{y}$ 的值为（）

A、9 B、-9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
6. 下列运算中，正确的是（）

A、 ${(- x)}^{2} x^{3} = x^{6}$ B、 ${(- x)}^{3} \div x = x^{2}$ C、 $3 x^{2} y z \div (- x y) = - 3 x z$ D、 ${(a - b)}^{6} \div {(a - b)}^{3} = a^{3} - b^{3}$

查看试题解析
7. 下列运算正确的是（）

A、 $a^{3} \cdot a^{3} = 2 a^{6}$ B、 ${(a - 3)}^{2} = a^{2} - 6 a - 9$ C、 ${(a^{3})}^{2} = a^{6}$ D、 $(b + 2 a) (2 a - b) = b^{2} - 4 a^{2}$

查看试题解析
8. 若 $A \cdot (m^{2} - 3 n) = m^{3} - 3 m n$ ，则代数式 $A$ 为（）

A、 $m$ B、mn C、 $m n^{2}$ D、 $m^{2} n$

查看试题解析
9. 若 $(x + \frac{1}{2}) (2 x - n) = 2 x^{2} + m x + 2$ ，则 $m + n$ 的值为（）

A、-9 B、9 C、-3 D、1

查看试题解析
10. 计算 $2^{101} \times {0.5}^{100}$ 的结果是（）

A、1 B、2 C、0.5 D、10

查看试题解析

二、填空题

11. 四个长宽分别为a，b的小长方形（白色的）按如图所示的方式放置，形成了一个长、宽分别为m、n的大长方形，则下列各式不能表示图中阴影部分的面积是。

①mn-4ab ②mn-2ab-am ③an+2bn-4ab ④a²-2ab-am+mn

查看试题解析
12. 一个正方形的面积为 $x^{2} + 4 x + 4 (x > 0)$ ，则它的边长为

查看试题解析
13. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个多项式，形式如下：
$\times (- \frac{1}{2} x y) = 3 x^{2} y - x y^{2} + \frac{1}{2} x y ，$

则当 $x = \frac{2}{3} ， y = \frac{1}{2}$ 时，所捂多项式的值是

查看试题解析
14. 若 $x^{n} \cdot x^{n - 4} = x^{10}$ ，则 $n =$ .

查看试题解析
15. 已知 $27^{2} = a^{6} = 9^{b}$ ，则 $2 a^{2} + 2 a b$ 的值为.

查看试题解析
16. 计算（-4×10³）²×（-2×10³）³=.（结果用科学记数法表示）

查看试题解析

三、解答题

17. 阅读下列文字，并解决问题。
已知x²y=3，求2xy（x⁵y²-3x³y-4x）的值.
分析：考虑到满足x²y=3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x²y=3整体代入.
解：2xy（x⁵y²-3x³y-4x）
=2x⁶y³-6x⁴y²-8x²y
=2（x²y）³-6（x²y）²-8x²y，
将x²y=3代入
原式=2×3³-6×3²-8×3=-24.
请你用上述方法解决下面问题：
已知ab=3，求（2a³b²-3a²b+4a）·（-2b）的值.

查看试题解析
18. 小明化简（2x+1）（2x-1）-x（x+5）的过程如下，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程.
解：原式=2x²-1-x（x+5）……①
=2x²-1-x²+5x……②
=x²+5x-1.………③

查看试题解析
19. 某城市为了鼓励居民节约用水，对自来水用户按如下标准收费。若每月每户用水不超过a吨，以每吨m元收费；若用水超过a吨，则超过的部分以每吨2m元收费。现有一居民本月用水x吨，则应交水费多少元？

查看试题解析
20. 小明在做一个多项式除以 $\frac{1}{2}$ a的题时，由于粗心误认为乘 $\frac{1}{2}$ a，结果是8a⁴b-4a³+2a² ，那么你能知道正确的结果是多少吗？

查看试题解析
21. 小红家的收入分农业收入和其他收入两部分，今年农业收入是其他收入的1.5倍，预计明年农业收入将减少20%，而其他收入将增加40%，那么预计小红家明年的全年总收入是增加了还是减少了？

查看试题解析
22. 算式2(3+1)(3²+1)(3⁴+1)(3⁸+1)(3¹⁶+1)(3³²+1)+1计算的结果个位是几？

查看试题解析

四、综合题

23. 如图，从边长为a的正方形纸片中剪掉一个边长为b的正方形纸片（如图1），然后将剩余部分拼成一个长方形（如图2）．

(1)、探究：上述操作能验证的等式是．

(2)、应用：利用（1）中得出的等式，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \cdot \cdot \cdot (1 - \frac{1}{9^{2}}) (1 - \frac{1}{10^{2}})$ ．

查看试题解析
24.

(1)、若 $2 x + 3 y - 4 z + 1 = 0$ ，求 $9^{x} \cdot 27^{y} \div$ $81^{2}$ 的值.

(2)、若 $(x^{2} + n x + 3) (x^{2} - 3 x + m)$ 的展开式中不含 $x^{2}$ 和 $x^{3}$ 的项，求m，n的值.

查看试题解析
25. 计算下列各式.

(1)、 $(x - 1) (x + 1) =$ .

$(x - 1) (x^{2} + x + 1) =$ .

$(x - 1) (x^{3} + x^{2} + x + 1) =$ .

……

(2)、根据以上规律，直接写出下式的结果：
$(x - 1) (x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1) =$

(3)、你能否由此归纳出一般性的结论：
$(x - 1) (x^{n - 1} + x^{n - 2} + x^{n - 3} + \dots + x + 1) =$ （其中 $n$ 为正整数）；

(4)、根据(2)的结论写出 $1 + 2 + 2^{2} + 2^{3} + 2^{4} + \dots +$ $2^{35}$ 的结果.

查看试题解析