2022年初中数学苏科版《中考二轮复习》专题一 数与式、方程与不等式 1.2 二次根式
试卷更新日期:2022-04-08 类型:二轮复习
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 函数y= 中自变量x的取值范围是( )A、x≥3且x≠5 B、x>3且x≠5 C、x<3且x≠5 D、x≤3且x≠53. 如果关于x的一元二次方程 有两个不相等的实数根,那么k的取值范围是( )A、 B、 且 C、 且 D、 且4. 已知:a= ,b= ,则a与b的关系是( )A、a-b=0 B、a+b=0 C、ab=1 D、a2=b25. 已知方程x2- x+2m=0有两个实数根,则 的化简结果是( )A、m-1 B、m+1 C、1-m D、±(m-1)6. 若a+b=3,ab=1,则式子 的值为( )A、 B、 C、 D、7. 已知m= ,n= ,则代数式 的值为( )A、 3 B、3 C、5 D、98. 把代数式 中的 移到根号内,那么这个代数式等于( )A、 B、 C、 D、9. 对于任意的正数m、n定义运算※为:m※n= , 计算(3※2)×(8※12)的结果为( )A、2﹣4 B、2 C、2 D、2010. 对于 这样的根式,我们可以利用“配方法”进行化简: .运用同样的方法化简 的结果是( )A、 B、 C、 D、
二、填空题
-
11. 已知 与最简二次根式 是同类二次根式,则a的值是.12. 计算 的结果是.13. 计算 的结果是.14. 若x,y是实数,且 , 则的值为 .15. 已知 ,则 的值为16. △ABC中a,b,c为三角形的三边,则 .17. 若实数 满足 ,则 .18. 若关于x的代数式 有意义,且满足条件的所有整数x的和为10,则 的取值范围为.
三、解答题
-
19. 计算(1)、(2)、(3)、20. 已知实数 、 互为相反数, 、 互为倒数, 是 的整数部分, 是 的小数部分.求代数式 的值.21. 如图,a,b,c是数轴上三个点A、B、C所对应的实数.试化简: .
 22. 阅读下列材料,然后回答问题.
22. 阅读下列材料,然后回答问题.在进行二次根式运算时,形如 一样的式子,我们可以将其进一步化简: = = ,以上这种化简的步骤叫做分母有理化.
(1)、请用上述的方法化简 ;(2)、利用上面的解法,化简: .23. 阅读材料:基本不等式 ≤ (a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+ 有最小值,最小值是多少?
解:∵x>0, >0∴ ≥ ,即 ≥2 ,∴ ≥2
当且仅当x= ,即x=1时,x+ 有最小值,最小值为2.
请根据阅读材料解答下列问题:
(1)、已知x>0,则当x为时,代数式3x+ 的最小值为;(2)、已知a>0,b>0,a2+b2=7,则ab的最大值为(3)、已知矩形面积为9,求矩形周长的最小值.24. 数学教育家波利亚曾说:“对一个数学问题,改变它的形式,变换它的结构,直到发现有价值的东西,这是数学解题的一个重要原则”.材料一:平方运算和开方运算是互逆运算.如a2±2ab+b2=(a±b)2 , 那么 ,如何将双重二次根式 化简.我们可以把 转化为 完全平方的形式,因此双重二次根式 得以化简.
材料二:在直角坐标系xOy中,对于点P(x,y)和Q(x,y’)给出如下定义:若 则称点Q为点P的“横负纵变点”.例如:点(3,2)的“横负纵变点”为(3,2),点(﹣2,5)的“横负纵变点”为(﹣2,﹣5).问题:
(1)、点 的“横负纵变点”为 , 点 的“横负纵变点”为;(2)、化简: ;(3)、已知a为常数(1≤a≤2),点M( ,m)是关于x的函数 图像上的一点,点M’是点M的“横负纵变点”,求点M’的坐标.25. 甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形演化而成的,其中OA1=A1A2=A2A3=…=A7A8=1.细心观察图形,认真分析下列各式,然后解答问题:

( )2+1=2,S1= ;( )2+1=3,S2= ;( )2+1=4,S3= ;….
(1)、请用含有n(n是正整数)的等式表示上述变化规律,并计算出OA10的长;(2)、求出 的值.26. 如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a、b、c分别满足﹣(a﹣4)2≥0,c= +8. (1)、求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;(2)、直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;(3)、点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值.27. 如图1,已知点A(a,0),B(0,b),且a、b满足 ,▱ABCD的边AD与y轴交于点E,且E为AD中点,双曲线 经过C、D两点.
(1)、求直线y=bx+c的解析式并直接写出正方形OABC的对角线的交点D的坐标;(2)、直线y=bx+c沿x轴正方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;(3)、点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,求 的值.27. 如图1,已知点A(a,0),B(0,b),且a、b满足 ,▱ABCD的边AD与y轴交于点E,且E为AD中点,双曲线 经过C、D两点.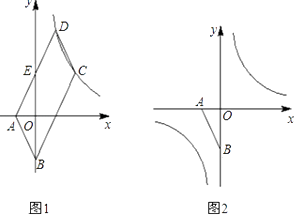 (1)、求k的值;(2)、点P在双曲线 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)、以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时, 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.
(1)、求k的值;(2)、点P在双曲线 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)、以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,当T在AF上运动时, 的值是否发生改变?若改变,求出其变化范围;若不改变,请求出其值,并给出你的证明.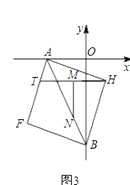 28. (性质认识)
28. (性质认识)如图,在函数 的图象上任取两点 、 向坐标轴作垂直,连接垂足 、 或 、 ,则一定有如下结论: , .
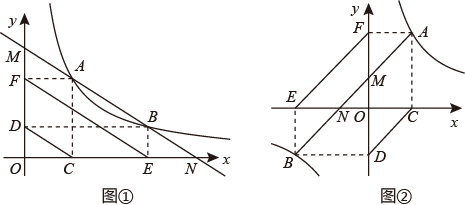 (1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .
(1)、(数学理解)如图①,借助(性质认知)的结论,猜想 (填“>”、“=”或“<”);(2)、如图②,借助(性质认知)的结论,证明: ;(3)、(问题解决)如图③,函数 的图象与过原点的直线相交于 、 两点,点 是第一象限内图象上的动点(点 在点 的左侧),直线 分别交于 轴、 轴于点 、 ,连接 分别交 轴、 轴于点 、 .请证明: .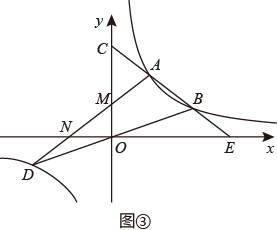 (4)、在第(3)问中,若 ,则 .
(4)、在第(3)问中,若 ,则 .