2022年浙教版数学七下期末复习阶梯训练：分式（优生加练）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、单选题

1. 若 $\frac{1}{2 y^{2} + 3 y + 7}$ 的值为 $\frac{1}{8}$ ,则 $\frac{1}{4 y^{2} + 6 y - 9}$ 的值是（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{17}$ C、 $- \frac{1}{7}$ D、 $\frac{1}{7}$

查看试题解析
2. 商家常将单价不同的A，B两种糖混合成“什锦糖”出售，记“什锦糖”的单价为：A，B两种糖的总价与A，B两种糖的总质量的比．现有两种“什锦糖”：一种是由相同千克数的A种糖和B种糖混合而成的“什锦糖”甲，另一种是由相同金额数的A种糖和B种糖混合而成的“什锦糖”乙．若B种糖比A种糖的单价贵40元/千克，“什锦糖”甲比“什锦糖”乙的单价贵5元/千克，则A种糖的单价为（）

A、50元/千克 B、60元/千克 C、70元/千克 D、80元/千克

查看试题解析
3. 已知三个数 $a ， b ， c$ 满足 $\frac{a b}{a + b} = \frac{1}{5}$ ， $\frac{b c}{b + c} = \frac{1}{6}$ ， $\frac{c a}{c + a} = \frac{1}{7}$ ，则 $\frac{a b c}{a b + b c + c a}$ 的值是（）

A、 $\frac{1}{9}$ B、 $\frac{1}{6}$ C、 $\frac{2}{15}$ D、 $\frac{1}{20}$

查看试题解析
4. 已知公式 $\frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$ （ $R_{1} \neq R_{2}$ ），则表示 $R_{1}$ 的公式是（）

A、 $R_{1} = \frac{R_{2} - R}{R R_{2}}$ B、 $R_{1} = \frac{R R_{2}}{R - R_{2}}$ C、 $R_{1} = \frac{R (R_{1} + R_{2})}{R_{2}}$ D、 $R_{1} = \frac{R R_{2}}{R_{2} - R}$

查看试题解析
5. 张华在一次数学活动中，利用“在面积一定的矩形中，正方形的周长最短”的结论，推导出“式子x+ $\frac{1}{x}$ （x＞0）的最小值是2”．其推导方法如下：在面积是1的矩形中设矩形的一边长为x，则另一边长是 $\frac{1}{x}$ ，矩形的周长是2（x+ $\frac{1}{x}$ ）；当矩形成为正方形时，就有x= $\frac{1}{x}$ （0＞0），解得x=1，这时矩形的周长2（x+ $\frac{1}{x}$ ）=4最小，因此x+ $\frac{1}{x}$ （x＞0）的最小值是2．模仿张华的推导，你求得式子 $\frac{x^{2} + 9}{x}$ （x＞0）的最小值是（）

A、2 B、1 C、6 D、10

查看试题解析
6. 若 $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{x + y}$ ，则 $\frac{y}{x}$ + $\frac{x}{y}$ 的值为（）

A、0 B、1 C、﹣1 D、无法计算

查看试题解析
7. 用甲乙两种饮料按照x：y(重量比)混合配制成一种新饮料，原来两种饮料成本是：甲每500克5元，乙每500克4元。现甲成本上升10%，乙下降10%，而新饮料成本恰好保持不变，则x：y= 。

A、4：5 B、3：4 C、2：3 D、1：2

查看试题解析
8. If m=2，then $\frac{{(- m)}^{3} \times {(- 1)}^{4} - | - 12 | \div [- {(- \frac{1}{m})}^{2}]}{- m^{2} \times (- \frac{1}{4}) + [1 - 3^{2} \times (- m)]}$ =（）

A、-2 B、-1 C、1 D、2

查看试题解析
9. 若x≠y，则下列分式化简中，正确的是（）

A、 $\frac{x + 2}{y + 2} = \frac{x}{y}$ B、 $\frac{x - 2}{y - 2} = \frac{x}{y}$ C、 $\frac{3 x}{3 y} = \frac{x}{y}$ D、 $\frac{x^{2}}{y^{2}} = \frac{x}{y}$

查看试题解析
10. 解方程 $\frac{2 x - 1}{3} = \frac{x + a}{2} - 1$ 时，小刚在去分母的过程中，右边的“-1”漏乘了公分母6，因而求得方程的解为 $x = 2$ ，则方程正确的解是（）

A、 $x = - 3$ B、 $x = - 2$ C、 $x = \frac{1}{3}$ D、 $x = - \frac{1}{3}$

查看试题解析

二、填空题

11. 已知 $\frac{x}{x^{2} - x + 1}$ ＝ $\frac{1}{7}$ ，则 $\frac{x^{2}}{x^{4} - x^{2} + 1}$ ＝．

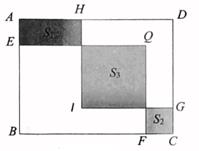
查看试题解析
12. 当整数x＝时，分式 $\frac{2 x + 2}{x^{2} - 1}$ 的值为正整数．

查看试题解析
13. 如图，在长方形ABCD中，AB=10，BC=13．E，F，G，H分别是线段AB，BC，CD，AD上的定点．现分别以BE，BF为边作长方形BEQF，以DG为边作正方形DGIH．若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形，且BE=DG，Q，I均在长方形ABCD内部．记图中的阴影部分面积分别为S₁ ， S₂ ， S₃ ．若 $\frac{S_{2}}{S_{1}} = \frac{3}{7}$ ，则S₃= ．

查看试题解析
14. 如果 $\frac{1}{(2 a - 1) (2 a + 1)} = \frac{m}{2 a - 1} + \frac{n}{2 a + 1}$ 对于自然数 $a \neq \frac{1}{2}$ 成立，则 $m =$ ， $n =$ ．

查看试题解析
15. 已知 $\frac{x}{x - 1} = \frac{y^{2} + 4 y - 2}{y^{2} + 4 y - 1}$ ，则的y²+4y+x值为．

查看试题解析
16. 一组按规律排列的式子： $- \frac{b^{2}}{a}$ ， $\frac{b^{5}}{a^{2}}$ ， $- \frac{b^{8}}{a^{3}}$ ， $\frac{b^{11}}{a^{4}}$ ，…（ab≠0），其中第7个式子是，第n个式子是（n为正整数）．

查看试题解析
17. 如图，甲，乙两人分别从A、B两地同时出发去往C地，在距离C地2500米处甲追上乙；若乙提前10分钟出发，则在距离C地1000米处甲追上乙。已知，乙每分钟走60米，那么甲的速度是每分钟米。

查看试题解析

三、解答题

18. 列方程解应用题：
甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？

查看试题解析
19. 某市在旧城改造过程中，需要整修一段全长2400米的道路，为了尽量减少施工对城市交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8小时完成任务，求原计划每小时修路的长度。

查看试题解析
20. 如果方程 $\frac{2 x - 3}{5} = \frac{2}{3} x - 2$ 与 $3 a - \frac{1}{4} = 3 (x + a) - 2 a$ 的解相同，求（a-3）²的值.

查看试题解析
21. 不改变分式的值，把下列分式的分子、分母中各项的系数化为整数．
（1） $\frac{\frac{1}{5} x - \frac{1}{10} y}{\frac{1}{3} x + \frac{1}{9} y}$ （2） $\frac{\frac{1}{2} x + \frac{1}{4} y}{\frac{1}{2} x - \frac{1}{3} y}$ ．

查看试题解析

四、综合题

22. 801班原有卫生区260平方米，现在由于某种原因变成了200平方米，因在打扫卫生时每分钟比原来少打扫15平方米，结果现在完成卫生任务的时间与原来的一样.
求：

(1)、原来每分钟打扫卫生多少平方米？

(2)、现在完成卫生任务要多少时间？

查看试题解析
23. 小明发现爸爸和妈妈的加油习惯不同，妈妈每次加油都说“师博，给我加200元油.”（油箱未加满）.而爸爸则说：“师傅，帮我把油箱加满！”小明很好奇：现实生活中油价常有变动，爸爸妈妈不同的加油方式，哪种方式会更省钱呢？现以两次加油为例来研究.设爸爸妈妈第一次加油油价为x元/升，第二次加油油价为y元/升.

(1)、求妈妈两次加油的总量和两次加油的平均价格.（用含x.y的代数式表示）

(2)、爸爸和妈妈的两种加油方式中，谁的加油方式更省钱？用所学数学知识说明理由.

查看试题解析
24. 2020年由于新冠肺炎爆发，为预防疫情专家提出了“勤洗手，戴口罩” 的措施，口罩在市场上供不应求，生产口罩的主要材料是熔喷布。已知1吨熔喷布可以生产105万只医用一次性口罩，或者60万只KN95口罩。某生产熔喷布的企业要求在规定时间内完成100吨熔喷布的订单，为提高产量，现对生产车间进行改造，改造后每天比改造前多生产4吨熔喷布，结果在规定时间内多生产了40吨熔喷布。

(1)、现有一批熔喷布，若全部用来生产医用一次性口罩则可以生产420万只，则这批熔喷布全部用来生产KN95口罩则可以生产万只；

(2)、求该企业改造后熔喷布的日产量和企业要求规定的天数。

查看试题解析
25. 增根是一个数学用语，其定义为在方程变形时，有时可能产生不适合原方程的根.对于分式方程： $\frac{2}{x - 3} + \frac{m x}{x^{2} - 9} = \frac{3}{x + 3}$

(1)、若该分式方程有增根，则增根为.

(2)、在（1）的条件下，求出 $m$ 的值.

查看试题解析