2022年浙教版数学七下期中复习阶梯训练：因式分解（优生集训）

试卷更新日期：2022-04-08 类型：复习试卷

进入出卷网下载

一、综合题

1. 分解因式：

(1)、 $a^{4} - 1$

(2)、 $- x^{3} + 6 x^{2} - 9 x$

查看试题解析
2. 分解因式：

(1)、 $y^{2} - 6 y + 9$

(2)、 $2 x^{2} - 8$

查看试题解析
3. 分解因式：

(1)、^{$x^{3} - 4 x^{2} y + 4 x y^{2}$}

(2)、 $- a^{2} + b^{2} - a + b$

查看试题解析
4. 对多项式(a²-4a+2)(a²-4a+6)+4进行因式分解时，小亮先设a²-4a=b，代
入原式后得：

原式=(b+2)(h+6)+4

=b²+8b+16

=(b+4)²

=(a²-4a+4)²

(1)、小亮在因式分解时巧妙运用了以下那种数学思想：__________；

A、整体换元思想 B、数形结合思想 C、分类讨论思想

(2)、请指出上述因式分解存在的问题并直接写出正确结果；

(3)、请参考以上方法对多项式(4a²+4a)(4a²+4a+2)+1进行因式分解。

查看试题解析
5. 若a+b＝3，ab＝1.
求

(1)、a²+b²；

(2)、（a﹣b）²；

(3)、ab³+a³b.

查看试题解析
6.

(1)、因式分解：（x-y）（3x-y）+2x（3x-y）；

(2)、设 y=kx，是否存在实数 k，使得上式的化简结果为 x²？求出所有满足条件的 k 的值．若不能，请说明理由．

查看试题解析
7. 已知 ${\begin{matrix} x = a \\ y = 1 \end{matrix}$ 是方程 $3 x + b y = \sqrt{5}$ 的解.

(1)、当 $a = 2 \sqrt{5}$ 时，求 $b$ 的值.

(2)、求 $9 a^{2} + 6 a b + b^{2} + 1$ 的值.

查看试题解析
8. 下面是某同学对多项式（x²-4x+2）（x²-4x+6）+4进行因式分解的过程．
解：设x²-4x=y，

原式=（y+2）（y+6）+4 （第一步）

=y²+8y+16 （第二步）

=（y+4）²（第三步）

=（x²-4x+4）²（第四步）

(1)、该同学第二步到第三步运用了因式分解的______．

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学因式分解的结果是否彻底？．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果．

(3)、请你模仿以上方法尝试对多项式（x²-2x）（x²-2x+2）+1进行因式分解．

查看试题解析
9. 在求代数式的值时，当单个字母不能或不用求出时，可把已条件作为一个整体，通过整体代入，实现降次、消元、归零、约分等，快速求得其结果．如：已知 ${(a - b)}^{2} = 49$ ， $a b = 18$ ，求代数式 $a^{2} + b^{2}$ 的值．可以这样思考：
因为 ${(a - b)}^{2} = 49$ ， $a b = 18$

所以 $a^{2} + b^{2} - 2 a b = 49$

即 $a^{2} + b^{2} - 2 \times 18 = 49$

所以 $a^{2} + b^{2} = 49 + 2 \times 18 = 85$

举一反三：

(1)、已知 ${(a - b)}^{2} = 12$ ， ${(a + b)}^{2} = 28$ ，求 $a b$ 的值．

(2)、已知 $a + \frac{1}{a} = 4$ ，则 $a^{4} + \frac{1}{a^{4}}$ 的值．

(3)、已知 $x^{2} + x = 1$ ，求 $x^{4} + 2 x^{3} - x^{2} - 2 x + 2019$ 的值．

查看试题解析
10. 下面是某同学对多项式（x²﹣4x+2）（x²﹣4x+6）+4进行因式分解的过程
解：设x²﹣4x＝y，

原式＝（y+2）（y+6）+4　（第一步）

＝y²+8y+16　（第二步）

＝（y+4）²（第三步）

＝（x²﹣4x+4）²（第四步）

(1)、该同学第二步到第三步运用了因式分解的（填序号）．

A、提取公因式 B、平方差公式 C、两数和的完全平方公式 D、两数差的完全平方公式

(2)、该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？．（填“是”或“否”）如果否，直接写出最后的结果．

(3)、请你模仿以上方法尝试对多项式（x²﹣2x）（x²﹣2x+2）+1进行因式分解．

查看试题解析
11. 解答题

(1)、根据如图所示的图形写出一个恒等代数式；

(2)、已知x- $\frac{1}{x}$ =3(其中x>0)，求x+ $\frac{1}{x}$ 的值.

查看试题解析
12. 阅读材料题：在因式分解中，有一类形如x²+（m+n）x+mn的多项式，其常数项是两个因数的积，而它的一次项系数恰是这两个因数的和，则我们可以把它分解成x²+（m+n）x+mn＝（x+m）（x+n）．
例如：x²+5x+6＝x²+（2+3）x+2×3＝（x+2）（x+3）．

运用上述方法分解因式：

(1)、x²+6x+8；

(2)、x²﹣x﹣6；

(3)、x²﹣5xy+6y²；

(4)、请你结合上述的方法，对多项式x³﹣2x²﹣3x进行分解因式．

查看试题解析
13. 将式子4x+（3x﹣x）=4x+3x﹣x，4x﹣（3x﹣x）=4x﹣3x+x分别反过来，你得到两个怎样的等式？

(1)、比较你得到的等式，你能总结添括号的法则吗？

(2)、根据上面你总结出的添括号法则，不改变多项式﹣3x⁵﹣4x²+3x³﹣2的值，把它的后两项放在：
①前面带有“+”号的括号里；
②前面带有“﹣”号的括号里．
③说出它是几次几项式，并按x的降幂排列．

查看试题解析
14. 因式分解：

(1)、 $a^{2} - 16$

(2)、 $2 x^{3} y - 4 x^{2} y^{2} + 2 x y^{3}$

查看试题解析
15. 分解因式：

(1)、 $2 x^{2} - 4 x y + 2 y^{2}$

(2)、 $m^{2} (m - n) + (n - m)$

查看试题解析
16. 把下列各式分解因式：

(1)、 $x {(x - y)}^{2} - 2 {(y - x)}^{2}$ ；

(2)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
17. 分解因式：

(1)、3a³－6a²+3a．

(2)、a²(x－y)+b²(y－x)．

查看试题解析
18. 分解因式：

(1)、 $4 x^{2} - 8 x y + 2 x$ ；

(2)、 $a^{4} - 8 a^{2} + 16$

查看试题解析
19. 综合题

(1)、因式分解：4x²﹣16

(2)、解方程组 ${\begin{matrix} 3 x + 2 y = 7 ① \\ 4 x - y = 13 ② \end{matrix}$ ．

查看试题解析
20. 分解因式：

(1)、3a³﹣6a²+3a．

(2)、a²（x﹣y）+b²（y﹣x）．

查看试题解析
21.
教材中，在计算如图1所示的正方形ABCD的面积时，分别从两个不同的角度进行了操作：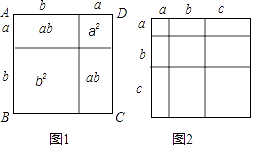

（i）把它看成是一个大正方形，则它的面积为（a+b）²；

（ii）把它看成是2个小长方形和2个小正方形组成的，则它的面积为a²+2ab+b²；因此，可得到等式：（a+b）²=a²+2ab+b² ．

(1)、类比教材中的方法，由图2中的大正方形可得等式：．

(2)、
试在图2右边空白处画出面积为2a²+3ab+b²的长方形的示意图（标注好a，b），由图形可知，多项式2a²+3ab+b²可分解因式为：．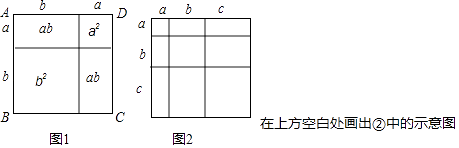

(3)、若将代数式（a₁+a₂+a₃+…+a₂₀）²展开后合并同类项，得到多项式N，则多项式N的项数一共有项．

查看试题解析
22. 分解因式

(1)、a³﹣2a²+a

(2)、a²（x﹣y）+16（y﹣x）

查看试题解析
23. 分解因式

(1)、21a³b﹣35a²b³

(2)、﹣x²+ $\frac{1}{4}$ y²

(3)、（2a﹣b）²+8ab．

查看试题解析