2022年浙教版数学七下期中复习阶梯训练:整式的乘除(优生集训)
试卷更新日期:2022-04-08 类型:复习试卷
一、综合题
-
1. 已知2a·3b·167c=2004,其中a,b,c为正整数。(1)、求a,b,c的值;(2)、求(a-b-c)2021的值。2. 两个边长分别为a和b的正方形( a<b<a),如图1所示放置,其未重合部分(阴影)的面积为S1 , 若在图1的右下角再摆放一个边长为b的小正方形(如图2),两个小正方形重合部分(阴影)面积为S2 .
 (1)、用含a , b的代数式分别表示S1 , S2;(2)、若a+b=15,ab=5,求S1+S2的值;(3)、当S1+S2=64时,求出图3中阴影部分的面积S3 .3. 探究规律,解决问题:(1)、化简: , .(2)、化简: ,写出化简过程.(3)、化简: . (n为正整数, 为 项多项式)(4)、利用以上结果,计算 的值.4. 乘法公式的探究及应用.
(1)、用含a , b的代数式分别表示S1 , S2;(2)、若a+b=15,ab=5,求S1+S2的值;(3)、当S1+S2=64时,求出图3中阴影部分的面积S3 .3. 探究规律,解决问题:(1)、化简: , .(2)、化简: ,写出化简过程.(3)、化简: . (n为正整数, 为 项多项式)(4)、利用以上结果,计算 的值.4. 乘法公式的探究及应用.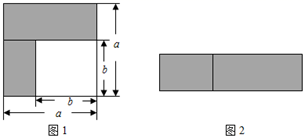 (1)、如上图1可以求出阴影部分的面积是;(2)、如上图2若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是;(3)、比较图1、图2的阴影部分面积,则可以得到乘法公式;(用含a,b的式子表示)(4)、小明展示了以下例题:计算: .
(1)、如上图1可以求出阴影部分的面积是;(2)、如上图2若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是;(3)、比较图1、图2的阴影部分面积,则可以得到乘法公式;(用含a,b的式子表示)(4)、小明展示了以下例题:计算: .解:原式
= .
在数学学习中,要学会观察,尝试从不同角度分析问题,这样才能学会数学.请计算: .
5. 在整式乘法的学习过程中,我们常常利用图形的面积对运算结果加以说明.例如由图①中图形的面积可以得到等式: (1)、利用图②中图形的面积关系,写出一个正确的等式:;(2)、计算 的值,并画出几何图形进行说明.6. 【发现问题】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助我们更容易理解数学问题.
(1)、利用图②中图形的面积关系,写出一个正确的等式:;(2)、计算 的值,并画出几何图形进行说明.6. 【发现问题】数形结合是解决数学问题的一种重要的思想方法,借助图的直观性,可以帮助我们更容易理解数学问题.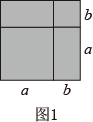

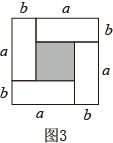

例如,求图1阴影部分的面积,可以得到乘法公式(a+b)2=a2+2ab+b2
请解答下列问题:
(1)、请写出求图2阴影部分的面积能解释的乘法公式(直接写出乘法公式即可)(2)、用4个全等的、长和宽分别为a、b的长方形,拼摆成如图3的正方形,请你观察求图3中阴影部分的面积,蕴含的相等关系,写出三个代数式:(a+b)2、(a-b)2、ab之间的等量关系式(直接写出等量关系式即可)(3)、【自主探索】小明用图4中x张边长为a的正方形,y张边长为b的正方形,z张宽为a,长为b的长方形纸片拼出一个面积为(3a+2b)(2a+3b)长方形,请在下面方框中画出图形,并计算x+z=
(4)、【拓展迁移】事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图5表示的是一个边长为a+b的正方体,请你根据图5求正方体的体积,写出一个代数恒等式:
 7. 乘法公式的探究及应用.
7. 乘法公式的探究及应用. (1)、如图 1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较图 1,图 2 的阴影部分面积,可以得到乘法公式(用式子表达)(4)、应用所得的公式计算:(1﹣ )(1﹣ )(1﹣ )…(1﹣ )(1﹣ )8.(1)、对于算式;
(1)、如图 1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较图 1,图 2 的阴影部分面积,可以得到乘法公式(用式子表达)(4)、应用所得的公式计算:(1﹣ )(1﹣ )(1﹣ )…(1﹣ )(1﹣ )8.(1)、对于算式;不用计算器,你能计算出来吗?直接写出计算结果.
(2)、你计算结果的个位数字是 .(3)、根据(1)推测 .9.(1)、先化简,再求值:6x2y(﹣2xy+y3)÷xy2 , 其中x=2,y=﹣1;(2)、已知 , .分别求 , 的值;10. 上数学课时,王老师在讲完乘法公式(a+b)2=a2+2ab+b2的多种运用后,要求同学们运用所学知识解答:求代数式x2+4x+5的最小值?同学们经过交流、讨论,最后总结出如下解答方法;
解:x2+4x+5=x2+4x+4+1=(x+2)2+1, ∵(x+2)2≥0, ∴当x=-2时,(x+2)2的值最小,最小值是0,
∴(x+2)2+1≥1,∴当(x+2) 2=0时,(x+2) 2+1的值最小,最小值是1,∴x2+4x+5的最小值是1。
请你根据上述方法,解答下列各题:
(1)、知识再现:当x=_时, 代数式x2-6x+12的最小值是_;(2)、知识运用:若y=-x2+2x-3,当x=时,y有最_值(填“大”或“小”),这个值是_(3)、知识拓展:若-x2+3x+y+5=0,求y+x的最小值。11. 如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分裁剪拼成一个长方形(如图2所示).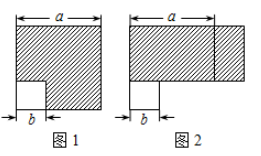 (1)、如图1,阴影部分的面积为;(2)、如图2,阴影部分(长方形)的宽为 , 长为 , 面积为;(3)、比较图1、图2阴影部分的面积,可以得到公式:;(4)、请应用这个公式完成下列各题:
(1)、如图1,阴影部分的面积为;(2)、如图2,阴影部分(长方形)的宽为 , 长为 , 面积为;(3)、比较图1、图2阴影部分的面积,可以得到公式:;(4)、请应用这个公式完成下列各题:①已知4m2﹣n2=12,2m+n=4,求2m﹣n的值;
②计算:5(6+1)(62+1)(64+1)(68+1)(616+1)+1.
12.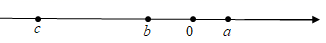 (1)、有理数 , , 在数轴上的位置如图所示,化简: .(2)、已知 与 的积不含 项和 项,求关于 的方程 的解.13. 如图①所示是一个长为 ,宽为 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形,根据这一操作过程回答下列问题:
(1)、有理数 , , 在数轴上的位置如图所示,化简: .(2)、已知 与 的积不含 项和 项,求关于 的方程 的解.13. 如图①所示是一个长为 ,宽为 的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形,根据这一操作过程回答下列问题: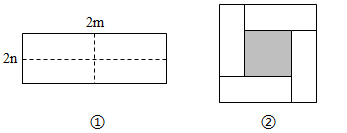 (1)、图②中阴影部分的正方形的边长为;(2)、请用两种方法表示图②中阴影部分的面积.
(1)、图②中阴影部分的正方形的边长为;(2)、请用两种方法表示图②中阴影部分的面积.方法一:;方法二:;
(3)、观察图②,写出代数式 、 、 之间的等量关系式:;(4)、计算: .14. 在下列横线上用含有a,b的代数式表示相应图形的面积.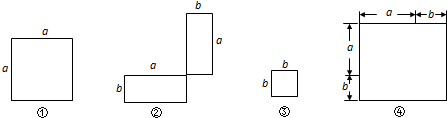 (1)、①;②;③;④.(2)、通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:;(3)、利用(2)的结论计算20192+2×2019×1+1的值.15. (知识生成)通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形 .把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:a2-b2 , 图2中阴影部分面积可表示为(a+b)(a-b),因为两个图中的阴影部分面积是相同的,所以可得到等式:a2-b2=(a+b)(a-b);
(1)、①;②;③;④.(2)、通过拼图,你发现前三个图形的面积与第四个图形面积之间有什么关系?请用数学式子表示:;(3)、利用(2)的结论计算20192+2×2019×1+1的值.15. (知识生成)通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形 .把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:a2-b2 , 图2中阴影部分面积可表示为(a+b)(a-b),因为两个图中的阴影部分面积是相同的,所以可得到等式:a2-b2=(a+b)(a-b);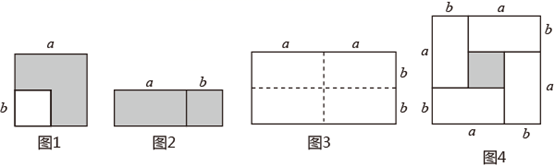
(拓展探究)图3是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.
(1)、用两种不同方法表示图4中阴影部分面积:方法1: , 方法2:;
(2)、由(1)可得到一个关于(a+b)2、(a-b)2、ab的的等量关系式是;(3)、若a+b=10,ab=5,则(a-b)2=;(4)、(知识迁移)
如图5,将左边的几何体上下两部分剖开后正好可拼成如右图的一个长方体.根据不同方法表示它的体积也可写出一个代数恒等式:. 16. 已知 , , .(1)、当 , 时, , .(2)、当 , 时, , .(3)、观察(1)和(2)的结果,可以得出结论: (n为正整数).(4)、此性质可以用来进行积的乘方运算,反之仍然成立.如 , ,….应用上述等式,求 的值.17. 如图1,边长为 的大正方形有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)
16. 已知 , , .(1)、当 , 时, , .(2)、当 , 时, , .(3)、观察(1)和(2)的结果,可以得出结论: (n为正整数).(4)、此性质可以用来进行积的乘方运算,反之仍然成立.如 , ,….应用上述等式,求 的值.17. 如图1,边长为 的大正方形有一个边长为 的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示)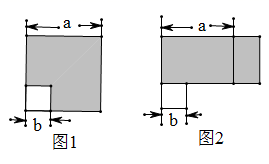 (1)、如图1,可以求出阴影部分的面积是(写成平方差的形式)(2)、如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是.(写成多项式乘法形式)(3)、比较左、右两图的阴影部分面积,可以得到公式.(4)、请应用这个公式完成下列各题:
(1)、如图1,可以求出阴影部分的面积是(写成平方差的形式)(2)、如图2,若将阴影部分裁剪下来,重新拼成一个长方形,它的宽是 , 长是 , 面积是.(写成多项式乘法形式)(3)、比较左、右两图的阴影部分面积,可以得到公式.(4)、请应用这个公式完成下列各题:①已知 , ,则 .
②计算:
③计算:
18. 小明和小亮玩纸片拼图游戏,发现利用图1中的三种材料各若干可以拼出一些长方形来解释某些等式.例如图2可以解释的等式为(a+2b)(a+b)=a2+3ab+2b2 .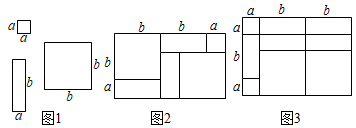 (1)、图3可以解释的等式为;(2)、请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2 , 画出你拼出的正方形示意图;(3)、要拼出一个长为a+3b , 宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片块,长为b , 宽为a的长方形纸片块,边长为b的正方形纸片块.19. 如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
(1)、图3可以解释的等式为;(2)、请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2 , 画出你拼出的正方形示意图;(3)、要拼出一个长为a+3b , 宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片块,长为b , 宽为a的长方形纸片块,边长为b的正方形纸片块.19. 如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2
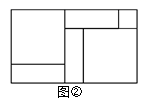 (1)、取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虚框中画出图形 , 并根据图形回答(2a+b)(a+2b)=
(1)、取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虚框中画出图形 , 并根据图形回答(2a+b)(a+2b)= (2)、若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2 . 根据你画的长方形,可得到恒等式(3)、如图③,大正方形的边长为m , 小正方形的边长为n , 若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式___________填写选项).
(2)、若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2 . 根据你画的长方形,可得到恒等式(3)、如图③,大正方形的边长为m , 小正方形的边长为n , 若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下正确的关系式___________填写选项). A、xy = B、x+y=m C、x2-y2=m·n D、x2+y2 =20. 某同学利用若干张正方形纸片进行以下操作:(1)、从边长为a的正方形纸片中减去一个边长为b的小正方形,如图1,再沿线段AB把纸片剪开,最后把剪成的两张纸片拼成如图2的等腰梯形,这一过程所揭示的公式是.
A、xy = B、x+y=m C、x2-y2=m·n D、x2+y2 =20. 某同学利用若干张正方形纸片进行以下操作:(1)、从边长为a的正方形纸片中减去一个边长为b的小正方形,如图1,再沿线段AB把纸片剪开,最后把剪成的两张纸片拼成如图2的等腰梯形,这一过程所揭示的公式是.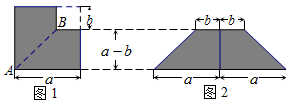 (2)、先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出两张边长分别为a和b的长方形纸片,如图3,最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式?
(2)、先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出两张边长分别为a和b的长方形纸片,如图3,最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式? (3)、先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出三张边长分别为a和占的长方形纸片,如图5,你能否把图5中所有纸片拼成一个长方形?
(3)、先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片,再剪出三张边长分别为a和占的长方形纸片,如图5,你能否把图5中所有纸片拼成一个长方形?如果可以,请画出草图,并写出相应的等式.如果不能,请说明理由.
 21. 在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.
21. 在边长为a的正方形中减掉一个边长为b的小正方形(a>b)把余下的部分再剪拼成一个长方形.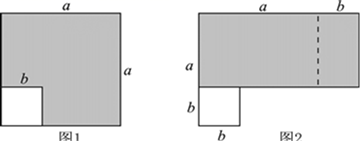 (1)、如图1,阴影部分的面积是:;
(1)、如图1,阴影部分的面积是:;如图2,是把图1重新剪拼成的一个长方形,阴影部分的面积是:;
比较两阴影部分面积,可以得到一个公式是:;
(2)、运用你所得到的公式,计算:97×10322. 如图1是一个长为 ,宽为 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). (1)、图2中的阴影部分的面积为 ;(2)、观察图2请你写出 , , 之间的等量关系是;(3)、根据(2)中的结论,若 , ,则 ;(4)、实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式 .在图形上把每一部分的面积标写清楚.23. 我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的.课本上由拼图用几何图形的面积来验证了乘法公式,一些代数恒等式也能用这种形式表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积表示.
(1)、图2中的阴影部分的面积为 ;(2)、观察图2请你写出 , , 之间的等量关系是;(3)、根据(2)中的结论,若 , ,则 ;(4)、实际上我们可以用图形的面积表示许多恒等式,下面请你设计一个几何图形来表示恒等式 .在图形上把每一部分的面积标写清楚.23. 我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,对几何图形做出代数解释和用几何图形的面积表示代数恒等式是互逆的.课本上由拼图用几何图形的面积来验证了乘法公式,一些代数恒等式也能用这种形式表示,例如(2a+b)(a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积表示.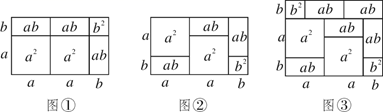 (1)、填一填:请写出图③所表示的代数恒等式:;(2)、画一画:试画出一个几何图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.24. 从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).
(1)、填一填:请写出图③所表示的代数恒等式:;(2)、画一画:试画出一个几何图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.24. 从边长为 a 的正方形剪掉一个边长为 b 的正方形(如图 1),然后将剩余部分拼成一个长方形(如图 2).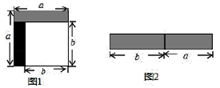 (1)、上述操作能验证的等式是_______(请选择正确的一个)A、a2﹣2ab+b2 =(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2 +ab=a(a+b)(2)、若 x2 ﹣9y2=12,x+3y=4,求 x﹣3y 的值;(3)、计算: .25. 好学小东同学,在学习多项式乘以多项式时发现:( x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为: x•2x•3x=3x3 , 常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x .
(1)、上述操作能验证的等式是_______(请选择正确的一个)A、a2﹣2ab+b2 =(a﹣b)2 B、a2﹣b2=(a+b)(a﹣b) C、a2 +ab=a(a+b)(2)、若 x2 ﹣9y2=12,x+3y=4,求 x﹣3y 的值;(3)、计算: .25. 好学小东同学,在学习多项式乘以多项式时发现:( x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为: x•2x•3x=3x3 , 常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是: ×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x .请你认真领会小东同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)、计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为 .(2)、( x+6)(2x+3)(5x-4)所得多项式的二次项系数为 .(3)、若计算(x2+x+1)(x2-3x+a)(2x-1)所得多项式不含一次项,求a的值;(4)、若(x+1)2021=a0x2021+a1x2020+a2x2019+···+a2020x+a2021 , 则a2020= .